dwt2
単一レベル 2 次元離散ウェーブレット変換
構文
説明
例
入力引数
出力引数
アルゴリズム
イメージの 2 次元ウェーブレット分解のアルゴリズムは 1 次元の場合と同様です。2 次元のウェーブレット関数とスケーリング関数は、1 次元のウェーブレット関数とスケーリング関数のテンソル積を取ることで得られます。このような 2 次元の DWT は、4 つの成分 (レベル j + 1 の Approximation と 3 つの方向 (水平、垂直、対角方向) の Detail) におけるレベル j の Approximation 係数の分解になります。次のチャートに、イメージの基本的な分解ステップを示します。

ここで、
 — 列をダウンサンプリング: 偶数のインデックスが付いた列を維持
— 列をダウンサンプリング: 偶数のインデックスが付いた列を維持 — 行をダウンサンプリング: 偶数のインデックスが付いた行を維持
— 行をダウンサンプリング: 偶数のインデックスが付いた行を維持 — フィルター X でエントリの行を畳み込み
— フィルター X でエントリの行を畳み込み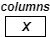 — フィルター X でエントリの列を畳み込み
— フィルター X でエントリの列を畳み込み
分解は、Approximation 係数をイメージ s と等しくなるように設定 (cA0 = s) することで初期化されます。
メモ
畳み込みに基づくアルゴリズムによる信号の端点の影響に対処するために、1 次元および 2 次元の DWT では dwtmode で管理されるグローバル変数を使用します。この変数で、使用される信号拡張モードの種類が定義されます。使用可能なオプションとしては、ゼロ パディング拡張や対称拡張 (既定のモード) があります。
参照
[1] Daubechies, Ingrid. Ten Lectures on Wavelets. CBMS-NSF Regional Conference Series in Applied Mathematics 61. Philadelphia, Pa: Society for Industrial and Applied Mathematics, 1992.
[2] Mallat, S.G. “A Theory for Multiresolution Signal Decomposition: The Wavelet Representation.” IEEE Transactions on Pattern Analysis and Machine Intelligence 11, no. 7 (July 1989): 674–93. https://doi.org/10.1109/34.192463.
[3] Meyer, Y. Wavelets and Operators. Translated by D. H. Salinger. Cambridge, UK: Cambridge University Press, 1995.
拡張機能
バージョン履歴
R2006a より前に導入




