このページの翻訳は最新ではありません。ここをクリックして、英語の最新版を参照してください。

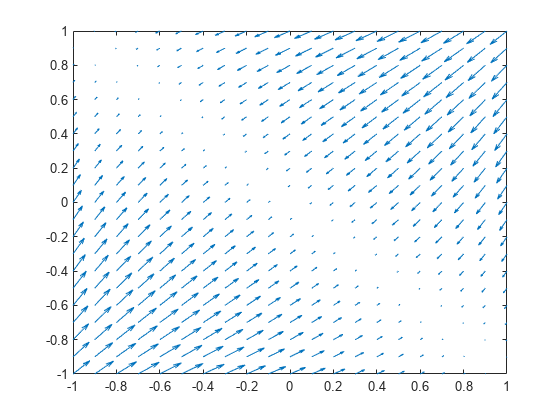
gradient

シンボリックなスカラー場の勾配ベクトル

構文

g = gradient(f,v)

g = gradient(f)

説明

g = gradient(f,v) は、直交座標のベクトル v について、シンボリックなスカラー場 f の勾配ベクトルを返します。

g = gradient(f) は、スカラー場 f のシンボリック変数から作成された既定のベクトルについて、f の勾配ベクトルを返します。

例

関数の勾配を求める

ベクトル v に対するスカラー関数 f の勾配は、v の各要素に対する f の 1 次偏導関数のベクトルです。

ベクトル [x,y,z] について f(x,y,z) の勾配ベクトルを求めます。勾配は、以下の成分をもつベクトルとなります。

syms x y z
f(x,y,z) = 2*y*z*sin(x) + 3*x*sin(z)*cos(y);
v = [x,y,z];
gradient(f,v)

ans(x, y, z) = 
$$\left(\begin{array}{c}3\hspace{0.17em}\cos \left(y\right)\hspace{0.17em}\sin \left(z\right)+2\hspace{0.17em}y\hspace{0.17em}z\hspace{0.17em}\cos \left(x\right)\\ 2\hspace{0.17em}z\hspace{0.17em}\sin \left(x\right)-3\hspace{0.17em}x\hspace{0.17em}\sin \left(y\right)\hspace{0.17em}\sin \left(z\right)\\ 2\hspace{0.17em}y\hspace{0.17em}\sin \left(x\right)+3\hspace{0.17em}x\hspace{0.17em}\cos \left(y\right)\hspace{0.17em}\cos \left(z\right)\end{array}\right)$$

関数の勾配のプロット

関数 f(x,y) の勾配を求め、矢印 (速度) 表示でプロットします。

ベクトル [x,y] について f(x,y) の勾配ベクトルを求めます。勾配は、以下の成分をもつベクトル g となります。

syms x y
f = -(sin(x) + sin(y))^2;
v = [x y];
g = gradient(f,v)

g = 
$$\left(\begin{array}{c}-2\hspace{0.17em}\cos \left(x\right)\hspace{0.17em}\left(\sin \left(x\right)+\sin \left(y\right)\right)\\ -2\hspace{0.17em}\cos \left(y\right)\hspace{0.17em}\left(\sin \left(x\right)+\sin \left(y\right)\right)\end{array}\right)$$

ここで、これらの成分によって定義されるベクトル場をプロットします。MATLAB® には、このタスクのためにプロット関数quiverが用意されています。この関数ではシンボリック引数は受け入れられません。まず、g の成分の式にあるシンボリック変数を数値で置き換えます。次に quiver を使用します。

[X,Y] = meshgrid(-1:.1:1,-1:.1:1);
G1 = subs(g(1),v,{X,Y});
G2 = subs(g(2),v,{X,Y});
quiver(X,Y,G1,G2)

行列乗算の勾配

R2021b 以降

シンボリック行列変数を使用して、スカラーを返す行列乗算を定義します。

syms X Y [3 1] matrix
A = Y.'*X

A = $$Y^{\mathrm{T}}\hspace{0.17em}X$$

$$X$$ についての行列乗算の勾配を求めます。

gX = gradient(A,X)

gX = $$Y$$

$$Y$$ についての行列乗算の勾配を求めます。

gY = gradient(A,Y)

gY = $$X$$

多変数関数の勾配

R2021b 以降

次の多変数関数の勾配を求めます。

$$f(x)={\sin }^2(x_{1,1})+{\sin }^2(x_{1,2})+{\sin }^2(x_{1,3})$$

これを、ベクトル $$x=[x_{1,1},x_{1,2},x_{1,3}]$$ について行います。

シンボリック行列変数を使用して、関数 $$f$$ とその勾配を、ベクトル $$x$$ で表現します。

syms x [1 3] matrix
f = sin(x)*sin(x).'

f = $$\sin \left(x\right)\hspace{0.17em}{\sin \left(x\right)}^{\mathrm{T}}$$

g = gradient(f,x)

g = $$2\hspace{0.17em}\left(\cos \left(x\right)\odot {\mathrm{I}}_3\right)\hspace{0.17em}{\sin \left(x\right)}^{\mathrm{T}}$$

$$x$$ の要素で勾配を表現するには、symmatrix2sym を使用して、結果をシンボリック スカラー変数のベクトルに変換します。

g = symmatrix2sym(g)

g = 
$$\left(\begin{array}{c}2\hspace{0.17em}\cos \left(x_{1,1}\right)\hspace{0.17em}\sin \left(x_{1,1}\right)\\ 2\hspace{0.17em}\cos \left(x_{1,2}\right)\hspace{0.17em}\sin \left(x_{1,2}\right)\\ 2\hspace{0.17em}\cos \left(x_{1,3}\right)\hspace{0.17em}\sin \left(x_{1,3}\right)\end{array}\right)$$

また、$$f$$ と $$x$$ をスカラー変数のシンボリック式に変換して、関数 gradient の入力として使用することもできます。

g = gradient(symmatrix2sym(f),symmatrix2sym(x))

g = 
$$\left(\begin{array}{c}2\hspace{0.17em}\cos \left(x_{1,1}\right)\hspace{0.17em}\sin \left(x_{1,1}\right)\\ 2\hspace{0.17em}\cos \left(x_{1,2}\right)\hspace{0.17em}\sin \left(x_{1,2}\right)\\ 2\hspace{0.17em}\cos \left(x_{1,3}\right)\hspace{0.17em}\sin \left(x_{1,3}\right)\end{array}\right)$$

勾配を含むベクトル微積分恒等式の求解

R2023a 以降

シンボリック行列変数 $\mathit{X}$ として 3 行 1 列のベクトルを作成します。$\mathit{X}$ の既存の定義を維持したまま、$\mathit{X}$ の関数であるスカラー場をシンボリック行列関数 $A\left(\mathit{X}\right)$ として作成します。

syms X [3 1] matrix
syms A(X) [1 1] matrix keepargs

$\mathit{X}$ について $A\left(\mathit{X}\right)$ の勾配を求めます。関数 gradient は未評価の式を返します。

gradA = gradient(A,X)

gradA(X) = $${\nabla }_X\mathrm{ }A\left(X\right)$$

$A\left(\mathit{X}\right)$ の勾配の発散が $A\left(\mathit{X}\right)$ のラプラシアン、つまり ${\nabla }_{\mathit{X}}\cdot {\nabla }_{\mathit{X}}\mathit{A}\left(\mathit{X}\right)={\Delta }_{\mathit{X}}\mathit{A}\left(\mathit{X}\right)$ に等しいことを示します。

divOfGradA = divergence(gradA,X)

divOfGradA(X) = $${\Delta }_X\mathrm{ }A\left(X\right)$$

lapA = laplacian(A,X)

lapA(X) = $${\Delta }_X\mathrm{ }A\left(X\right)$$

$A\left(\mathit{X}\right)$ の勾配の回転がゼロ、つまり ${\nabla }_{\mathit{X}}\times {\nabla }_{\mathit{X}}\mathit{A}\left(\mathit{X}\right)=0_{3,1}$ であることを示します。

curlOfGradA = curl(gradA,X)

curlOfGradA(X) = $${\mathrm{0}}_{3,1}$$

入力引数

f — シンボリックなスカラー場

シンボリック式 | シンボリック関数 | シンボリック行列変数 | シンボリック行列関数

シンボリックなスカラー場。シンボリック式、シンボリック関数、シンボリック行列変数、またはシンボリック行列関数として指定します。

• f がシンボリック スカラー変数の関数であり、f が sym 型または symfun 型である場合、ベクトル v は sym 型または symfun 型でなければならない。

• f がシンボリック行列変数の関数であり、f が symmatrix 型または symfunmatrix 型である場合、ベクトル v は symmatrix 型または symfunmatrix 型でなければならない。

データ型: sym | symfun | symmatrix | symfunmatrix

v — 勾配を求める対象のベクトル

シンボリック スカラー変数のベクトル | シンボリック関数 | シンボリック行列変数 | シンボリック行列関数

勾配を求める対象のベクトル。シンボリック スカラー変数、シンボリック関数、シンボリック行列変数、またはシンボリック行列関数のベクトルとして指定します。

• v を指定せず、f がシンボリック スカラー変数の関数である場合、既定では、gradient は symvar(f) で定義された変数の順序で、f のシンボリック スカラー変数からベクトル v を構成する。

• v が symmatrix 型のシンボリック行列変数である場合、v は 1 行 N 列または N 行 1 列のサイズでなければならない。

• v がスカラーの場合、gradient(f,v) = diff(f,v) となる。

• v が sym([]) のような空のシンボリック オブジェクトの場合、gradient は、空のシンボリック オブジェクトを返します。

データ型: sym | symfun | symmatrix | symfunmatrix

制限

• 関数 gradient はテンソル微分をサポートしません。勾配がベクトルではなくテンソル場または行列である場合、関数 gradient はエラーを返します。

• 現在、Symbolic Math Toolbox™ は、シンボリック行列変数の関数 dot または関数 cross と、symmatrix 型および symfunmatrix 型の関数をサポートしていません。ベクトル微積分の恒等式がドット積またはクロス積を含む場合、ツールボックスは代わりに他のサポートされている関数でそれらの恒等式を表示します。シンボリック行列の変数と関数をサポートするすべての関数のリストを表示するには、コマンド methods symmatrix と methods symfunmatrix を使用します。

詳細

勾配ベクトル

ベクトル $$x=\left(x_1,x_2,\dots ,x_n\right)$$ に対する f(x) の勾配ベクトルは、f の 1 次偏導関数のベクトルです。

$${\nabla }_{x}f(x)=\left(\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\dots ,\frac{\partial f}{\partial x_n}\right)$$

バージョン履歴

R2011b で導入

R2023a: シンボリック行列関数の勾配の計算

関数 gradient は、入力引数として、symfunmatrix 型のシンボリック行列関数を受け入れます。例については、勾配を含むベクトル微積分恒等式の求解を参照してください。

R2021b: シンボリック行列変数の勾配の計算

関数 gradient は、入力引数として、symmatrix 型のシンボリック行列変数を受け入れます。例については、行列乗算の勾配および多変数関数の勾配を参照してください。

参考

curl | divergence | diff | hessian | jacobian | laplacian | potential | quiver | vectorPotential

×

例を開く

この例の変更されたバージョンがあります。編集された方の例を開きますか?

いいえ、変更されたバージョンを上書きします。 はい