fourier

シンボリック式またはシンボリック関数のフーリエ変換

構文

FT = fourier(f)

FT = fourier(f,transVar)

FT = fourier(f,var,transVar)

説明

FT = fourier(f) は、f のフーリエ変換を返します。既定では、関数 symvar は独立変数を決定し、w は変換変数です。

FT = fourier(f,transVar) は、w の代わりに transVar を変換変数として使用します。

FT = fourier(f,var,transVar) は、symvar(f,1) と w の代わりに var と transVar をそれぞれ独立変数および変換変数として使用します。

例

一般的な関数のフーリエ変換

一般的な関数のフーリエ変換を計算します。既定では、w に関して変換されます。

矩形パルス関数のフーリエ変換を求めます。

syms a b t
f = rectangularPulse(a,b,t);
FT = fourier(f)

FT = 
$$-\frac{\sin \left(a\hspace{0.17em}w\right)+\cos \left(a\hspace{0.17em}w\right)\hspace{0.17em}\mathrm{i}}{w}+\frac{\sin \left(b\hspace{0.17em}w\right)+\cos \left(b\hspace{0.17em}w\right)\hspace{0.17em}\mathrm{i}}{w}$$

単位インパルス (ディラックのデルタ関数) のフーリエ変換を求めます。

f = dirac(t);
FT = fourier(f)

FT = $$1$$

絶対値関数のフーリエ変換を求めます。

f = a*abs(t);
FT = fourier(f)

FT = 
$$-\frac{2\hspace{0.17em}a}{w^2}$$

ステップ関数 (ヘヴィサイド関数) のフーリエ変換を求めます。

f = heaviside(t);
FT = fourier(f)

FT = 
$$\pi \hspace{0.17em}\delta \text{<a href="matlab:doc symbolic/dirac">dirac</a>}\left(w\right)-\frac{\mathrm{i}}{w}$$

定数のフーリエ変換を求めます。

f = a;
FT = fourier(f)

FT = $$2\hspace{0.17em}\pi \hspace{0.17em}{\delta \text{<a href="matlab:doc symbolic/dirac">dirac</a>}}^{\prime }\left(w\right)\hspace{0.17em}\mathrm{i}$$

余弦関数のフーリエ変換を求めます。

f = a*cos(b*t);
FT = fourier(f)

FT = $$\pi \hspace{0.17em}a\hspace{0.17em}\left(\delta \text{<a href="matlab:doc symbolic/dirac">dirac</a>}\left(b+w\right)+\delta \text{<a href="matlab:doc symbolic/dirac">dirac</a>}\left(b-w\right)\right)$$

正弦関数のフーリエ変換を求めます。

f = a*sin(b*t);
FT = fourier(f)

FT = $$\pi \hspace{0.17em}a\hspace{0.17em}\left(\delta \text{<a href="matlab:doc symbolic/dirac">dirac</a>}\left(b+w\right)-\delta \text{<a href="matlab:doc symbolic/dirac">dirac</a>}\left(b-w\right)\right)\hspace{0.17em}\mathrm{i}$$

符号関数のフーリエ変換を求めます。

f = sign(t);
FT = fourier(f)

FT = 
$$-\frac{2\hspace{0.17em}\mathrm{i}}{w}$$

仮定なしで右側の指数関数のフーリエ変換を求めます。

f = exp(-t*abs(a))*heaviside(t);
FT = fourier(f)

FT = 
$$\frac{1}{\left|a\right|+w\hspace{0.17em}\mathrm{i}}-\left(\frac{\mathrm{sign}\left(\left|a\right|\right)}{2}-\frac{1}{2}\right)\hspace{0.17em}\mathrm{fourier}\left({\mathrm{e}}^{-t\hspace{0.17em}\left|a\right|},t,w\right)$$

a > 0 と仮定して右側の指数関数のフーリエ変換を求めます。フーリエ変換の計算後、仮定を消去します。

assume(a > 0)
FTwithAssumption = fourier(f)

FTwithAssumption = 
$$\frac{1}{a+w\hspace{0.17em}\mathrm{i}}$$

assume(a,"clear")

a > 0 と仮定して両側の指数関数のフーリエ変換を求めます。フーリエ変換の計算後、仮定を消去します。

assume(a > 0)
f = exp(-a*t^2);
FTwithAssumption = fourier(f)

FTwithAssumption = 
$$\frac{\sqrt{\pi }\hspace{0.17em}{\mathrm{e}}^{-\frac{w^2}{4\hspace{0.17em}a}}}{\sqrt{a}}$$

assume(a,"clear")

b と c が実数であると仮定してガウス関数のフーリエ変換を求めます。フーリエ変換の計算後、結果を単純化して仮定を消去します。

syms c
assume([b c],"real")
f = a*exp(-(t-b)^2/(2*c^2));
FT = fourier(f);
FTsimplified = simplify(FT)

FTsimplified = 
$$\sqrt{2}\hspace{0.17em}a\hspace{0.17em}\sqrt{\pi }\hspace{0.17em}{\mathrm{e}}^{-\frac{w\hspace{0.17em}\left(w\hspace{0.17em}{c}^2+2\hspace{0.17em}b\hspace{0.17em}\mathrm{i}\right)}{2}}\hspace{0.17em}\left|c\right|$$

assume([b c],"clear")

nu = 1 の第 1 種ベッセル関数のフーリエ変換を求めます。結果を単純化します。

syms x
f = besselj(1,x);
FT = fourier(f);
FTsimplified = simplify(FT)

FTsimplified = 
$$-\frac{2\hspace{0.17em}w\hspace{0.17em}\mathrm{rectangularPulse}\left(-1,1,-w\right)\hspace{0.17em}\mathrm{i}}{\sqrt{1-w^2}}$$

独立変数および変換変数の指定

exp(-t^2-x^2) のフーリエ変換を求めます。既定では、symvar は独立変数を決定し、w は変換変数です。ここで、symvar は x を選択します。

syms t x
f = exp(-t^2-x^2);
FT = fourier(f)

FT = 
$$\sqrt{\pi }\hspace{0.17em}{\mathrm{e}}^{-t^2-\frac{w^2}{4}}$$

変換変数として y を指定します。変数を 1 つだけ指定した場合、その変数は変換変数です。symvar が依然として独立変数を決定します。

syms y
FT = fourier(f,y)

FT = 
$$\sqrt{\pi }\hspace{0.17em}{\mathrm{e}}^{-t^2-\frac{y^2}{4}}$$

独立変数を t、変換変数を y としてそれぞれ指定します。

FT = fourier(f,t,y)

FT = 
$$\sqrt{\pi }\hspace{0.17em}{\mathrm{e}}^{-x^2-\frac{y^2}{4}}$$

矩形パルスとそのフーリエ変換のプロット

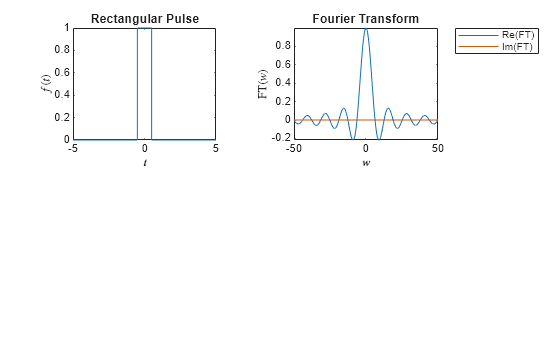
開始点が –1/2、終点が 1/2 の矩形パルスを作成します。

syms t
f1 = rectangularPulse(-1/2,1/2,t);

そのフーリエ変換を求めます。結果を単純化します。ここでは、フーリエ変換に実数部のみが含まれます。

FT1 = fourier(f1);
FT1 = simplify(FT1)

FT1 = 
$$\frac{2\hspace{0.17em}\sin \left(\frac{w}{2}\right)}{w}$$

fplot を使用して、矩形パルスを 2 行 2 列のタイル表示チャート レイアウトでプロットします。そのフーリエ変換の実数部と虚数部をプロットします。

tiledlayout(2,2)

nexttile
fplot(f1)
xlabel("$t$",Interpreter="latex")
ylabel("$f(t)$",Interpreter="latex")
title("Rectangular Pulse")

nexttile
fplot(real(FT1),[-50 50])
hold on
fplot(imag(FT1),[-50 50])
xlabel("$w$",Interpreter="latex")
ylabel("FT($w$)",Interpreter="latex")
title("Fourier Transform")
legend("Re(FT)","Im(FT)",Location="northeastoutside")

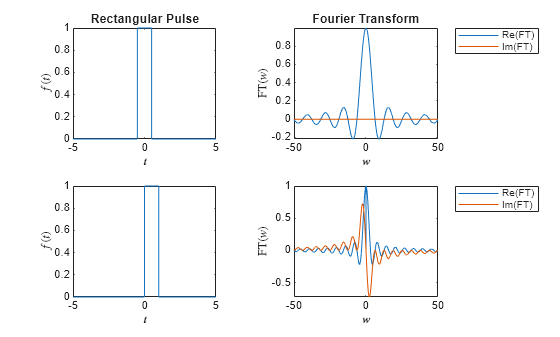
次に、開始点が 0、終点が 1 の別の矩形パルスを作成します。

f2 = rectangularPulse(0,1,t);

そのフーリエ変換を求めます。ここでは、フーリエ変換に実数部と虚数部の両方が含まれます。

FT2 = fourier(f2)

FT2 = 
$$\frac{\sin \left(w\right)+\cos \left(w\right)\hspace{0.17em}\mathrm{i}}{w}-\frac{\mathrm{i}}{w}$$

矩形パルスをプロットします。そのフーリエ変換の実数部と虚数部をプロットします。

nexttile
fplot(f2)
xlabel("$t$",Interpreter="latex")
ylabel("$f(t)$",Interpreter="latex")

nexttile
fplot(real(FT2),[-50 50])
hold on
fplot(imag(FT2),[-50 50])
xlabel("$w$",Interpreter="latex")
ylabel("FT($w$)",Interpreter="latex")
legend("Re(FT)","Im(FT)",Location="northeastoutside")

ディラックおよびヘヴィサイドの関数を含むフーリエ変換

t^3 のフーリエ変換を求めます。結果は、ディラックのデルタ関数の 3 次導関数で返されます。

syms t w
FT = fourier(t^3,t,w)

FT = $$-2\hspace{0.17em}\pi \hspace{0.17em}{\delta \text{<a href="matlab:doc symbolic/dirac">dirac</a>}}^{\prime \prime \prime }\left(w\right)\hspace{0.17em}\mathrm{i}$$

t0 に不連続点があるヘヴィサイド関数のフーリエ変換を求めます。

syms t0
FT = fourier(heaviside(t - t0),t,w)

FT = 
$${\mathrm{e}}^{-t_0\hspace{0.17em}w\hspace{0.17em}\mathrm{i}}\hspace{0.17em}\left(\pi \hspace{0.17em}\delta \text{<a href="matlab:doc symbolic/dirac">dirac</a>}\left(w\right)-\frac{\mathrm{i}}{w}\right)$$

フーリエ変換パラメーターの指定

詳細のセクションで説明するように、$$c$$ および $$s$$ はフーリエ変換のパラメーターです。既定では、fourier 関数は $$c=1$$ と $$s=-1$$ を使用します。ただし、これらのパラメーター値は sympref を使用して変更できます。

フーリエ変換のパラメーターの既定値を使用して、t*exp(-t^2) のフーリエ変換を計算します。

syms t w
f = t*exp(-t^2);
FT = fourier(f,t,w)

FT = 
$$-\frac{w\hspace{0.17em}\sqrt{\pi }\hspace{0.17em}{\mathrm{e}}^{-\frac{w^2}{4}}\hspace{0.17em}\mathrm{i}}{2}$$

sympref を使用して、フーリエ変換のパラメーターを c = 1 と s = 1 に変更し、変換を再計算します。結果が変わります。

sympref("FourierParameters",[1 1]);
FT = fourier(f,t,w)

FT = 
$$\frac{w\hspace{0.17em}\sqrt{\pi }\hspace{0.17em}{\mathrm{e}}^{-\frac{w^2}{4}}\hspace{0.17em}\mathrm{i}}{2}$$

フーリエ変換のパラメーターを c = 1/(2*pi) と s = 1 に変更し、変換を再計算します。結果が変わります。

sympref("FourierParameters",[1/(2*sym(pi)) 1]);
FT = fourier(f,t,w)

FT = 
$$\frac{w\hspace{0.17em}{\mathrm{e}}^{-\frac{w^2}{4}}\hspace{0.17em}\mathrm{i}}{4\hspace{0.17em}\sqrt{\pi }}$$

sympref を使用して設定したシンボリック設定は、現在およびこれ以降の MATLAB® セッションを通じて維持されます。FourierParameters を "default" に設定して、c および s の設定を既定値に戻します。

sympref("FourierParameters","default");

配列入力を使用したフーリエ変換

行列 M のフーリエ変換を求めます。同じサイズの行列を使用して、各行列要素の独立変数と変換変数を指定します。引数が非スカラーである場合、fourier は各要素に適用されます。

syms a b c d w x y z
M = [exp(x) 1; sin(y) 1i*z];
vars = [w x; y z];
transVars = [a b; c d];
FT = fourier(M,vars,transVars)

FT = 
$$\left(\begin{array}{cc}2\hspace{0.17em}\pi \hspace{0.17em}{\mathrm{e}}^x\hspace{0.17em}\delta \text{<a href="matlab:doc symbolic/dirac">dirac</a>}\left(a\right)& 2\hspace{0.17em}\pi \hspace{0.17em}\delta \text{<a href="matlab:doc symbolic/dirac">dirac</a>}\left(b\right)\\ -\pi \hspace{0.17em}\left(\delta \text{<a href="matlab:doc symbolic/dirac">dirac</a>}\left(c-1\right)-\delta \text{<a href="matlab:doc symbolic/dirac">dirac</a>}\left(c+1\right)\right)\hspace{0.17em}\mathrm{i}& -2\hspace{0.17em}\pi \hspace{0.17em}{\delta \text{<a href="matlab:doc symbolic/dirac">dirac</a>}}^{\prime }\left(d\right)\end{array}\right)$$

fourier をスカラーと非スカラーの両方の引数で呼び出した場合、スカラー拡張を使用して非スカラー引数と一致するようスカラー引数を拡張します。非スカラー引数のサイズは同じでなければなりません。

FT = fourier(x,vars,transVars)

FT = 
$$\left(\begin{array}{cc}2\hspace{0.17em}\pi \hspace{0.17em}x\hspace{0.17em}\delta \text{<a href="matlab:doc symbolic/dirac">dirac</a>}\left(a\right)& 2\hspace{0.17em}\pi \hspace{0.17em}{\delta \text{<a href="matlab:doc symbolic/dirac">dirac</a>}}^{\prime }\left(b\right)\hspace{0.17em}\mathrm{i}\\ 2\hspace{0.17em}\pi \hspace{0.17em}x\hspace{0.17em}\delta \text{<a href="matlab:doc symbolic/dirac">dirac</a>}\left(c\right)& 2\hspace{0.17em}\pi \hspace{0.17em}x\hspace{0.17em}\delta \text{<a href="matlab:doc symbolic/dirac">dirac</a>}\left(d\right)\end{array}\right)$$

計算不可能なフーリエ変換

fourier が入力を変換できない場合は、未評価の呼び出しが返されます。

syms f(t) w
FT = fourier(f,t,w)

FT = $$\mathrm{fourier}\left(f\left(t\right),t,w\right)$$

ifourier を使用して元の式を返します。

f = ifourier(FT,w,t)

f = $$f\left(t\right)$$

2 次元フーリエ変換

一連の 1 次元フーリエ変換を各独立変数に個別に適用することで、2 次元フーリエ変換を求めます。

この例では、フーリエ変換のパラメーターを $$c=1$$ と $$s=2\pi$$ に設定し、2 次元フーリエ変換の式が次を満たすようにします。

$\mathit{F}\left(\mathit{u},\mathit{v}\right)={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }\mathit{f}\left(\mathit{x},\mathit{y}\right){\mathit{e}}^{\mathit{i}\left(\mathit{2}\pi \mathrm{ux}+\mathit{2}\pi \mathrm{vy}\right)}\mathit{dx}\mathit{dy}$.

これらのパラメーターは sympref を使用して指定できます。

sympref("FourierParameters",[1 2*sym(pi)]);

幅が a、高さが b の原点に位置する 2 次元の単位矩形の 2 次元フーリエ変換を求めます。1 次元フーリエ変換を変数 $$x$$ に対して実行し、その後に変数 $$y$$ に対して実行します。結果を単純化します。

syms x y a b real
f(x,y) = rectangularPulse(-a/2,a/2,x)*rectangularPulse(-b/2,b/2,y);
syms u v
FT = fourier(f,x,u);
FT = fourier(FT,y,v);
FT = simplify(FT)

FT = 
$$\frac{\sin \left(\pi \hspace{0.17em}a\hspace{0.17em}u\right)\hspace{0.17em}\sin \left(\pi \hspace{0.17em}b\hspace{0.17em}v\right)}{u\hspace{0.17em}v\hspace{0.17em}{\pi }^2}$$

$$x$$ と $$y$$ の両方向の標準偏差が $$\sigma$$ である 2 次元ガウス関数のフーリエ変換を求めます。

syms sigma real
f(x,y) = 1/2/sym(pi)/sigma^2*exp((-x^2-y^2)/2/sigma^2);
syms u v
FT = fourier(f,x,u);
FT = fourier(FT,y,v);
FT = simplify(FT)

FT = $${\mathrm{e}}^{-2\hspace{0.17em}{\sigma }^2\hspace{0.17em}{\pi }^2\hspace{0.17em}\left(u^2+v^2\right)}$$

$$(x,y)=(0,a)$$ と $$(x,y)=(0,-a)$$ に位置する 2 点のソースのフーリエ変換を求めます。

f(x,y) = 1/2*dirac(x)*(dirac(y-a)+dirac(y+a));
FT = fourier(f,x,u);
FT = fourier(FT,y,v);
FT = simplify(FT)

FT = $$\cos \left(2\hspace{0.17em}\pi \hspace{0.17em}a\hspace{0.17em}v\right)$$

単位円の開口部のフーリエ変換を求めます。heaviside 関数を使用して単位円を定義します。

f(x,y) = heaviside(x^2+y^2-1);
FT = fourier(f,x,u);
FT = fourier(FT,y,v)

FT = $$\mathrm{fourier}\left(\mathrm{fourier}\left(\mathrm{heaviside}\left(x^2+y^2-1\right),x,u\right),y,v\right)$$

ここでは、fourier 関数が入力関数を変換できず、未評価の呼び出しが返されます。別の方法として、fft2関数を使用すると、2 次元フーリエ変換を数値的に求めることができます。円形の開口部の 2 次元フーリエ変換を求める方法の例については、2 次元フーリエ変換を参照してください。

sympref を使用して設定したシンボリック設定は、現在およびこれ以降の MATLAB セッションを通じて維持されます。既定の設定に戻します。

sympref("default");

入力引数

f — 入力

シンボリック式 | シンボリック関数 | シンボリック ベクトル | シンボリック行列

シンボリック式、シンボリック関数、シンボリック ベクトルまたはシンボリック行列で指定される入力。

transVar — 変換変数

w (既定値) | v | シンボリック変数 | シンボリック式 | シンボリック ベクトル | シンボリック行列

変換変数。シンボリック変数、シンボリック式、シンボリック ベクトルまたはシンボリック行列として指定します。この変数は、多くの場合 "周波数変数" と呼ばれます。既定では、fourier は w を使用します。w が f の独立変数の場合、fourier は v を使用します。

var — 独立変数

f の symvar (既定値) | シンボリック変数 | シンボリック ベクトル | シンボリック行列

独立変数。シンボリック変数、シンボリック ベクトルまたはシンボリック行列として指定します。この変数は、多くの場合 "時間変数" または "空間変数" と呼ばれます。この引数を指定しない場合、fourier は関数 symvar(f,1) を使用して独立変数を決定します。

詳細

フーリエ変換

変数 x の式 f = f(x) の点 w におけるフーリエ変換は

$$F\left(w\right)=c{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}f\left(x\right)e^{iswx}dx},$$

です。

ここで、c および s はフーリエ変換のパラメーターです。fourier 関数は c = 1 と s = –1 を使用します。

ヒント

• いずれかの引数が配列である場合、fourier は配列の全要素について要素単位で動作します。

• 1 番目の引数がシンボリック関数を含む場合、2 番目の引数はスカラーでなければなりません。

• 逆フーリエ変換を計算するには、ifourier を使用します。

• fourier は piecewise を変換しません。代わりに、関数 heaviside、rectangularPulse、または triangularPulse を使用して piecewise を書き換えてください。

参照

[1] Oberhettinger, Fritz. Tables of Fourier Transforms and Fourier Transforms of Distributions. Berlin, Heidelberg: Springer Berlin Heidelberg, 1990.

バージョン履歴

R2006a より前に導入

参考

関数

• ifourier | laplace | ilaplace | ztrans | iztrans | sympref | symvar

トピック

• フーリエ変換と逆フーリエ変換

外部の Web サイト

• Fourier Analysis (MathWorks Teaching Resources)