フーリエ変換と逆フーリエ変換

このページでは、Symbolic Math Toolbox™ でのフーリエ変換と逆フーリエ変換のワークフローを示します。単純な例については、fourier および ifourier を参照してください。ここでは、力によるビームの歪みを計算することで、フーリエ変換のワークフローを示します。関連する偏微分方程式は、フーリエ変換によって解きます。

フーリエ変換の定義

x の関数としての f(x) の w におけるフーリエ変換は以下になります。

$F (w) = \int_{- \infty}^{\infty} f (x) e^{- i w x} d x .$

逆フーリエ変換は以下になります。

$f (x) = \frac{1}{2 π} \int_{- \infty}^{\infty} F (w) e^{i w x} d w .$

概念: シンボリックワークフローの使用

シンボリックワークフローは、計算を数値形式の代わりにもともとのシンボリック形式で保持します。この手法は、解のプロパティについて理解し、厳密なシンボリック値を使用するのに役立ちます。数値結果が必要な場合や、シンボリック的に続行できない場合に限り、シンボリック変数に数値を代入します。詳細については、数値演算またはシンボリック演算の選択を参照してください。通常、手順は以下になります。

方程式を宣言する。
方程式を解く。
値を代入する。
結果をプロットする。
結果を解析する。

フーリエ変換を使用した梁のたわみの計算

方程式の定義

フーリエ変換は、常微分方程式および偏微分方程式の求解に利用できます。たとえば、弾力のある基礎に置かれた無限長の梁の 1 点に力を加えたときのたわみをモデル化できます。現実世界で対応する例は、基礎の上に敷かれた線路です。線路は無限長の梁であり、基礎には弾力があります。

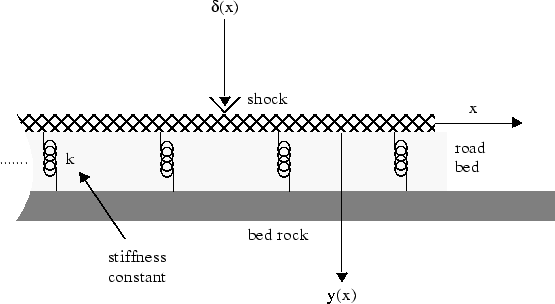
Illustration of a beam resting on elastic springs under a point force

以下により

E は梁 (つまり線路) の弾性です。
I は梁の断面の 2 次モーメントです。
k は基礎のバネ剛性です。

微分方程式は以下になります。

$\frac{d^{4} y}{d x^{4}} + \frac{k}{E I} y = \frac{1}{E I} δ (x), - \infty < x < \infty .$

関数 y(x) と変数を定義します。E、I および k が正であると仮定します。

syms Y(x) w E I k f
assume([E I k] > 0)

symunit を使用して単位を変数に代入します。

u = symunit;
Eu = E*u.Pa;    % Pascal
Iu = I*u.m^4;   % meter^4
ku = k*u.N/u.m^2;  % Newton/meter^2
X = x*u.m;
F = f*u.N/u.m;

微分方程式を定義します。

eqn = diff(Y,X,4) + ku/(Eu*Iu)*Y == F/(Eu*Iu)

eqn(x) =
diff(Y(x), x, x, x, x)*(1/[m]^4) + ((k*Y(x))/(E*I))*([N]/([Pa]*[m]^6)) == ...
        (f/(E*I))*([N]/([Pa]*[m]^5))

ディラックのデルタ関数 δ(x) で力 f を表します。

eqn = subs(eqn,f,dirac(x))

eqn(x) =
diff(Y(x), x, x, x, x)*(1/[m]^4) + ((k*Y(x))/(E*I))*([N]/([Pa]*[m]^6)) == ...
        (dirac(x)/(E*I))*([N]/([Pa]*[m]^5))

方程式の求解

eqn の両辺で fourier を使用して eqn のフーリエ変換を計算します。フーリエ変換により、微分が w の指数に変換されます。

eqnFT = fourier(lhs(eqn)) == fourier(rhs(eqn))

eqnFT =
w^4*fourier(Y(x), x, w)*(1/[m]^4) + ((k*fourier(Y(x), x, w))/(E*I))*([N]/([Pa]*[m]^6)) ...
        == (1/(E*I))*([N]/([Pa]*[m]^5))

方程式内の fourier(Y(x),x,w) を分離します。

eqnFT = isolate(eqnFT, fourier(Y(x),x,w))

eqnFT =
fourier(Y(x), x, w) == (1/(E*I*w^4*[Pa]*[m]^2 + k*[N]))*[N]*[m]

右辺の逆フーリエ変換を計算して Y(x) を計算します。結果を単純化します。

YSol = ifourier(rhs(eqnFT));
YSol = simplify(YSol)

YSol =
((exp(-(2^(1/2)*k^(1/4)*abs(x))/(2*E^(1/4)*I^(1/4)))*sin((2*2^(1/2)*k^(1/4)*abs(x) + ...
        pi*E^(1/4)*I^(1/4))/(4*E^(1/4)*I^(1/4))))/(2*E^(1/4)*I^(1/4)*k^(3/4)))*[m]

YSol を eqn に代入し、checkUnits 関数を使用して、YSol の次元が正しいことを確認します。checkUnits は、logical 1 (true) を返します。これは、eqn が同じ物理次元の互換性のある単位を持っていることを意味します。

checkUnits(subs(eqn,Y,YSol))

ans = 
  struct with fields:

    Consistent: 1
    Compatible: 1

separateUnits を使用して式を単位から切り離します。

YSol = separateUnits(YSol)

YSol =
(exp(-(2^(1/2)*k^(1/4)*abs(x))/(2*E^(1/4)*I^(1/4)))*sin((2*2^(1/2)*k^(1/4)*abs(x) + ...
        pi*E^(1/4)*I^(1/4))/(4*E^(1/4)*I^(1/4))))/(2*E^(1/4)*I^(1/4)*k^(3/4))

値の代入

値 E = 10⁶ Pa、I = 10^-3 m⁴、および k = 10⁶ N/m² を使用します。これらの値を YSol に代入し、16 桁の精度で vpa を使用して浮動小数点に変換します。

values = [1e6 1e-3 1e5];
YSol = subs(YSol,[E I k],values);
YSol = vpa(YSol,16)

YSol =
0.0000158113883008419*exp(-2.23606797749979*abs(x))*sin(2.23606797749979*abs(x) + ...
        0.7853981633974483)

結果のプロット

fplot を使用して結果をプロットします。

fplot(YSol)
xlabel('x')
ylabel('Deflection y(x)')

結果の解析

プロットは、1 点への力による梁のたわみが非常に局所的であることを示しています。たわみは衝撃点で最大であり、そこから急減しています。シンボリックな結果からは結果の特性が解析できます。数値結果ではこれは不可能です。

YSol は項の積であることに注意してください。sin を持つ項は、応答が周期的な振動動作であることを示しています。exp を持つ項は、衝撃点からの距離の増加と共に振動動作が指数減衰に従って急減することを示しています。

参考

外部の Web サイト

Fourier Analysis (MathWorks Teaching Resources)