ラプラス変換を使用した微分方程式の求解

このワークフローでは、Symbolic Math Toolbox™ でラプラス変換を使用して微分方程式を解きます。ラプラス変換の単純な例については、laplaceおよびilaplaceを参照してください。

定義: ラプラス変換

関数 $f (t)$ のラプラス変換は以下になります。

$F (s) = \int_{0}^{\infty} f (t) e^{- ts} dt .$

概念: シンボリックワークフローの使用

シンボリックワークフローは、計算を数値形式の代わりにもともとのシンボリック形式で保持します。この手法は、解のプロパティについて理解し、厳密なシンボリック値を使用するのに役立ちます。数値結果が必要な場合や、シンボリック的に続行できない場合に限り、シンボリック変数に数値を代入します。詳細は、数値演算またはシンボリック演算の選択を参照してください。通常、手順は以下になります。

方程式を宣言する。
方程式を解く。
値を代入する。
結果をプロットする。
結果を解析する。

ワークフロー: ラプラス変換を使用した RLC 回路の求解

方程式の宣言

ラプラス変換は、初期条件が指定された微分方程式の求解に利用できます。たとえば、以下のような抵抗-インダクタ-コンデンサ (RLC) 回路を解くことができます。

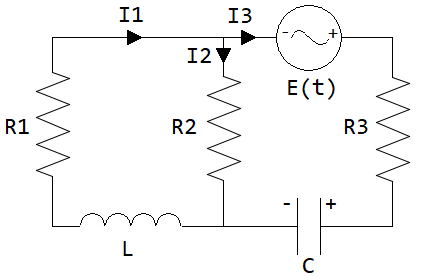
抵抗 (オーム): $R_{1}, R_{2}, R_{3}$
電流 (アンペア): $I_{1}, I_{2}, I_{3}$
インダクタンス (ヘンリー): $L$
静電容量 (ファラド): $C$
AC 電圧源 (ボルト): $E (t)$
コンデンサ電荷 (クーロン): $Q (t)$

キルヒホッフの電圧則および電流則を適用して、次の式を得ます。

$\begin{array}{l} I_{1} = I_{2} + I_{3} \\ L \frac{{dI}_{1}}{dt} + I_{1} R_{1} + I_{2} R_{2} = 0 \\ E (t) + I_{2} R_{2} - \frac{Q}{C} - I_{3} R_{3} = 0 \end{array}$

$I_{3} = d Q / d t$ (コンデンサが充電される割合) の関係を上の式に代入して、RLC 回路の微分方程式を得ます。

$\begin{array}{l} \frac{{dI}_{1}}{dt} - \frac{R_{2}}{L} \frac{dQ}{dt} = - \frac{R_{1} + R_{2}}{L} I_{1} \\ \frac{dQ}{dt} = \frac{1}{R_{2} + R_{3}} (E (t) - \frac{Q}{C}) + \frac{R_{2}}{R_{2} + R_{3}} I_{1} \end{array}$

変数を宣言します。物理量は正の値であるため、対応する仮定を変数に設定します。このときの $E (t)$ を 1 V の交流電圧とします。

syms L C I1(t) Q(t) s
R = sym('R%d',[1 3]);
assume([t L C R] > 0)
E(t) = 1*sin(t);        % AC voltage = 1 V

微分方程式を宣言します。

dI1 = diff(I1,t);
dQ = diff(Q,t);
eqn1 = dI1 - (R(2)/L)*dQ == -(R(1)+R(2))/L*I1

eqn1(t) = 
 $\frac{\partial}{\partial t} I_{1} (t) - \frac{R_{2} \frac{\partial}{\partial t} Q (t)}{L} = - \frac{I_{1} (t) (R_{1} + R_{2})}{L}$

eqn2 = dQ == (1/(R(2)+R(3))*(E-Q/C)) + R(2)/(R(2)+R(3))*I1

eqn2(t) = 
 $\frac{\partial}{\partial t} Q (t) = \frac{\sin (t) - \frac{Q (t)}{C}}{R_{2} + R_{3}} + \frac{R_{2} I_{1} (t)}{R_{2} + R_{3}}$

方程式の求解

eqn1 と eqn2 のラプラス変換を計算します。

eqn1LT = laplace(eqn1,t,s)

eqn1LT = 
 $s laplace (I_{1} (t), t, s) - I_{1} (0) + \frac{R_{2} (Q (0) - s laplace (Q (t), t, s))}{L} = - \frac{(R_{1} + R_{2}) laplace (I_{1} (t), t, s)}{L}$

eqn2LT = laplace(eqn2,t,s)

eqn2LT = 
 $s laplace (Q (t), t, s) - Q (0) = \frac{R_{2} laplace (I_{1} (t), t, s)}{R_{2} + R_{3}} + \frac{\frac{C}{s^{2} + 1} - laplace (Q (t), t, s)}{C (R_{2} + R_{3})}$

関数 solve は、シンボリック変数のみを解きます。したがって、solve を使用するには、最初に laplace(I1(t),t,s) と laplace(Q(t),t,s) を変数 I1_LT と Q_LT に置き換えます。

syms I1_LT Q_LT
eqn1LT = subs(eqn1LT,[laplace(I1,t,s) laplace(Q,t,s)],[I1_LT Q_LT])

eqn1LT = 
 $I_{1, LT} s - I_{1} (0) + \frac{R_{2} (Q (0) - Q_{LT} s)}{L} = - \frac{I_{1, LT} (R_{1} + R_{2})}{L}$

eqn2LT = subs(eqn2LT,[laplace(I1,t,s) laplace(Q,t,s)],[I1_LT Q_LT])

eqn2LT = 
 $Q_{LT} s - Q (0) = \frac{I_{1, LT} R_{2}}{R_{2} + R_{3}} - \frac{Q_{LT} - \frac{C}{s^{2} + 1}}{C (R_{2} + R_{3})}$

I1_LT と Q_LT について方程式を解きます。

eqns = [eqn1LT eqn2LT];
vars = [I1_LT Q_LT];
[I1_LT, Q_LT] = solve(eqns,vars)

I1_LT = 
 $\frac{L I_{1} (0) - R_{2} Q (0) + C R_{2} s + L s^{2} I_{1} (0) - R_{2} s^{2} Q (0) + C L R_{2} s^{3} I_{1} (0) + C L R_{3} s^{3} I_{1} (0) + C L R_{2} s I_{1} (0) + C L R_{3} s I_{1} (0)}{(s^{2} + 1) (R_{1} + R_{2} + L s + C L R_{2} s^{2} + C L R_{3} s^{2} + C R_{1} R_{2} s + C R_{1} R_{3} s + C R_{2} R_{3} s)}$

Q_LT = 
 $\frac{C (R_{1} + R_{2} + L s + L R_{2} I_{1} (0) + R_{1} R_{2} Q (0) + R_{1} R_{3} Q (0) + R_{2} R_{3} Q (0) + L R_{2} s^{2} I_{1} (0) + L R_{2} s^{3} Q (0) + L R_{3} s^{3} Q (0) + R_{1} R_{2} s^{2} Q (0) + R_{1} R_{3} s^{2} Q (0) + R_{2} R_{3} s^{2} Q (0) + L R_{2} s Q (0) + L R_{3} s Q (0))}{(s^{2} + 1) (R_{1} + R_{2} + L s + C L R_{2} s^{2} + C L R_{3} s^{2} + C R_{1} R_{2} s + C R_{1} R_{3} s + C R_{2} R_{3} s)}$

I1_LT と Q_LT の逆ラプラス変換を計算して、 $I_{1}$ と $Q$ を計算します。結果を単純化します。出力は長いため非表示にします。

I1sol = ilaplace(I1_LT,s,t);
Qsol = ilaplace(Q_LT,s,t);
I1sol = simplify(I1sol);
Qsol = simplify(Qsol);

値の代入

結果をプロットする前に、回路の各要素の数値でシンボリック変数を置き換えます。 $R_{1} = 4 Ω$ 、 $R_{2} = 2 Ω$ 、 $R_{3} = 3 Ω$ 、 $C = 1 / 4 F$ 、 $L = 1.6 H$ とします。初期電流を $I_{1} (0) = 2 A$ 、初期電荷を $Q (0) = 2 C$ と仮定します。

vars = [R L C I1(0) Q(0)];
values = [4 2 3 1.6 1/4 2 2];
I1sol = subs(I1sol,vars,values)

I1sol = 
 $\frac{200 \cos (t)}{8161} + \frac{405 \sin (t)}{8161} + \frac{16122 e^{- \frac{81 t}{40}} (\cosh (\frac{\sqrt{1761} t}{40}) - \frac{742529 \sqrt{1761} \sinh (\frac{\sqrt{1761} t}{40})}{14195421})}{8161}$

Qsol = subs(Qsol,vars,values)

Qsol = 
 $\frac{924 \sin (t)}{8161} - \frac{1055 \cos (t)}{8161} + \frac{17377 e^{- \frac{81 t}{40}} (\cosh (\frac{\sqrt{1761} t}{40}) + \frac{1109425 \sqrt{1761} \sinh (\frac{\sqrt{1761} t}{40})}{30600897})}{8161}$

結果のプロット

電流 I1sol と電荷 Qsol をプロットします。2 つの異なる時間間隔 $0 \leq t \leq 15$ および $2 \leq t \leq 25$ を使用して、過渡と定常状態の両方の動作を示します。

subplot(2,2,1)
fplot(I1sol,[0 15])                      
title('Current')
ylabel('I1(t)')
xlabel('t')

subplot(2,2,2)
fplot(Qsol,[0 15])                        
title('Charge')
ylabel('Q(t)')
xlabel('t')

subplot(2,2,3)
fplot(I1sol,[2 25])                  
title('Current')
ylabel('I1(t)')
xlabel('t')
text(3,-0.1,'Transient')
text(15,-0.07,'Steady State')

subplot(2,2,4)
fplot(Qsol,[2 25])                        
title('Charge')
ylabel('Q(t)')
xlabel('t')
text(3,0.35,'Transient')
text(15,0.22,'Steady State')

Figure contains 4 axes objects. Axes object 1 with title Current contains an object of type functionline. Axes object 2 with title Charge contains an object of type functionline. Axes object 3 with title Current contains 3 objects of type functionline, text. Axes object 4 with title Charge contains 3 objects of type functionline, text.

結果の解析

最初は、電流と電荷は指数関数的に減衰します。しかし、長期的にはこれらは振動性です。これらの動作はそれぞれ "過渡" および "定常状態" と呼ばれます。シンボリックな結果からは結果の特性が解析できます。数値結果ではこれは不可能です。

I1sol と Qsol を目視で検査します。これらは、項の和です。children を使用して項を求めます。次に、[0 15] にわたって項をプロットして項の寄与を求めます。プロットは、過渡および定常状態の項を示します。

I1terms = children(I1sol);
I1terms = [I1terms{:}];
Qterms = children(Qsol);
Qterms = [Qterms{:}];

figure;
subplot(1,2,1)
fplot(I1terms,[0 15])
ylim([-0.5 2.5])
title('Current terms')

subplot(1,2,2)
fplot(Qterms,[0 15])
ylim([-0.5 2.5])
title('Charge terms')

Figure contains 2 axes objects. Axes object 1 with title Current terms contains 3 objects of type functionline. Axes object 2 with title Charge terms contains 3 objects of type functionline.

このプロットは、I1sol が 1 つの過渡と 1 つの定常状態の項を持ち、Qsol が 1 つの過渡と 2 つの定常状態の項を持つことを示します。目視の検査により、I1sol と Qsol が exp 関数を含む項を持つことがわかります。この項によって過渡の指数減衰が発生すると推定します。has を使用して exp の項を確認し、I1sol と Qsol 内の過渡と定常状態の項を分離します。

I1transient = I1terms(has(I1terms,'exp'))

I1transient = 
 $\frac{16122 e^{- \frac{81 t}{40}} (\cosh (\frac{\sqrt{1761} t}{40}) - \frac{742529 \sqrt{1761} \sinh (\frac{\sqrt{1761} t}{40})}{14195421})}{8161}$

I1steadystate = I1terms(~has(I1terms,'exp'))

I1steadystate = 
 $(\begin{array}{c} \frac{200 \cos (t)}{8161} & \frac{405 \sin (t)}{8161} \end{array})$

同様に、Qsol を過渡および定常状態の項に分離します。この結果は、シンボリック計算が問題の解析にどのように役立つかを示しています。

Qtransient = Qterms(has(Qterms,'exp'))

Qtransient = 
 $\frac{17377 e^{- \frac{81 t}{40}} (\cosh (\frac{\sqrt{1761} t}{40}) + \frac{1109425 \sqrt{1761} \sinh (\frac{\sqrt{1761} t}{40})}{30600897})}{8161}$

Qsteadystate = Qterms(~has(Qterms,'exp'))

Qsteadystate = 
 $(\begin{array}{c} - \frac{1055 \cos (t)}{8161} & \frac{924 \sin (t)}{8161} \end{array})$