伝達関数の出力の高調波解析

この例では、出力信号の周波数の係数に対する閉形式解を求めます。出力信号は、解析的非線形伝達関数からの入力により得られます。

この例では、次の Symbolic Math Toolbox™ 機能を使用します。

taylorを使用したテイラー級数展開
式の操作と単純化

目的

解析しやすいように、回路理論から簡単な要素 (順方向バイアス動作の理想的なダイオード) を選びました。出力の電流 I は入力 V に指数関数的に依存します。ダイオードは混合器や増幅器などのデバイスの製作に利用されます。その場合、出力の高調波構成を理解しておくと、デバイス特性を記述したり設計仕様に適合させたりするうえで役立ちます。

syms Is V Vo real;
I = Is*(exp(V/Vo) - 1)

I =  $Is (e^{V / Vo} - 1)$

V が周波数 LO と RF の 2 つの信号の線形結合の場合、非線形伝達関数では LO と RF を組み合わせて、高調波周波数結合の組み合わせ (freqs = {LO, 2LO, RF, 2RF, LO-RF, LO-2RF,...}) のデータで出力を作成します。

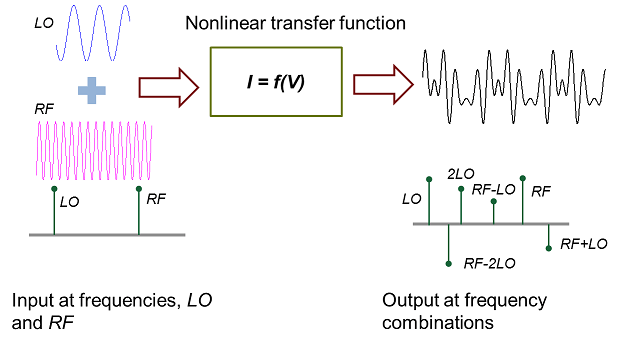
この例の目的は、出力における freqs の係数を決めることです。

入力信号の定義

入力信号は、2 つの余弦信号の線形結合です。

syms c1 c2 t LO RF real;
input = c1*cos(LO*t) + c2*cos(RF*t)

input =  $c_{1} \cos (LO t) + c_{2} \cos (RF t)$

調波周波数結合空間の定義

以下のように、harmCombinations は入力周波数 LO と RF の整数倍結合の組み合わせです。対象領域は制限されており、LO と RF の方向において 3 高調波によりそれぞれ定義されています。

n = 3;
harmCombinations = [kron((0:n)',ones(n*2+1,1)),repmat((-n:n)',n+1,1)];
freqs = harmCombinations*[LO;RF];

最初の n 個の周波数は負の調波周波数のため、入力信号が実数であることを考慮すると不要となります。

freqs = freqs(n+1:end)

freqs = 
 $(\begin{array}{c} 0 \\ RF \\ 2 RF \\ 3 RF \\ LO - 3 RF \\ LO - 2 RF \\ LO - RF \\ LO \\ LO + RF \\ LO + 2 RF \\ LO + 3 RF \\ 2 LO - 3 RF \\ 2 LO - 2 RF \\ 2 LO - RF \\ 2 LO \\ 2 LO + RF \\ 2 LO + 2 RF \\ 2 LO + 3 RF \\ 3 LO - 3 RF \\ 3 LO - 2 RF \\ 3 LO - RF \\ 3 LO \\ 3 LO + RF \\ 3 LO + 2 RF \\ 3 LO + 3 RF \end{array})$

テイラー展開

対象の周波数スペクトルに対応するには、I(V) に対して第 4 次のテイラー級数で十分です。

s = taylor(I, V, 'Order', 4)

s = 
 $\frac{Is V^{2}}{2 {Vo}^{2}} + \frac{Is V^{3}}{6 {Vo}^{3}} + \frac{Is V}{Vo}$

周波数 LO とRF の入力信号の組み合わせを使用し、cos(LO*t) と cos(RF*t) を用いて f を表します。

f0 = subs(s, V, input);
f = expand(f0)

f = 
 $\begin{array}{l} \frac{Is {c_{1}}^{2} σ_{2}}{2 {Vo}^{2}} + \frac{Is {c_{1}}^{3} {\cos (LO t)}^{3}}{6 {Vo}^{3}} + \frac{Is {c_{2}}^{2} σ_{1}}{2 {Vo}^{2}} + \frac{Is {c_{2}}^{3} {\cos (RF t)}^{3}}{6 {Vo}^{3}} + \frac{Is c_{1} \cos (LO t)}{Vo} + \frac{Is c_{2} \cos (RF t)}{Vo} + \frac{Is c_{1} c_{2} \cos (LO t) \cos (RF t)}{{Vo}^{2}} + \frac{Is c_{1} {c_{2}}^{2} \cos (LO t) σ_{1}}{2 {Vo}^{3}} + \frac{Is {c_{1}}^{2} c_{2} σ_{2} \cos (RF t)}{2 {Vo}^{3}} \\ where \\ σ_{1} = {\cos (RF t)}^{2} \\ σ_{2} = {\cos (LO t)}^{2} \end{array}$

余弦の単一のべき乗を用いて f を書き換えます。

f = combine(f, 'sincos')

f = 
 $\frac{Is {c_{1}}^{2}}{4 {Vo}^{2}} + \frac{Is {c_{2}}^{2}}{4 {Vo}^{2}} + \frac{Is c_{1} \cos (LO t)}{Vo} + \frac{Is c_{2} \cos (RF t)}{Vo} + \frac{Is {c_{1}}^{2} \cos (2 LO t)}{4 {Vo}^{2}} + \frac{Is {c_{1}}^{3} \cos (LO t)}{8 {Vo}^{3}} + \frac{Is {c_{1}}^{3} \cos (3 LO t)}{24 {Vo}^{3}} + \frac{Is {c_{2}}^{2} \cos (2 RF t)}{4 {Vo}^{2}} + \frac{Is {c_{2}}^{3} \cos (RF t)}{8 {Vo}^{3}} + \frac{Is {c_{2}}^{3} \cos (3 RF t)}{24 {Vo}^{3}} + \frac{Is c_{1} {c_{2}}^{2} \cos (LO t)}{4 {Vo}^{3}} + \frac{Is {c_{1}}^{2} c_{2} \cos (RF t)}{4 {Vo}^{3}} + \frac{Is c_{1} c_{2} \cos (LO t + RF t)}{2 {Vo}^{2}} + \frac{Is c_{1} c_{2} \cos (LO t - RF t)}{2 {Vo}^{2}} + \frac{Is c_{1} {c_{2}}^{2} \cos (LO t - 2 RF t)}{8 {Vo}^{3}} + \frac{Is c_{1} {c_{2}}^{2} \cos (LO t + 2 RF t)}{8 {Vo}^{3}} + \frac{Is {c_{1}}^{2} c_{2} \cos (2 LO t + RF t)}{8 {Vo}^{3}} + \frac{Is {c_{1}}^{2} c_{2} \cos (2 LO t - RF t)}{8 {Vo}^{3}}$

係数の抽出と表示

非定数 (つまり、cos(freq*t) 形の非 DC 調波周波数項) を取得します。

cosFreqs = cos(expand(freqs*t));
terms = collect(setdiff(cosFreqs', sym(1)));

DC を含むすべての調波周波数項の係数を抽出します。

newvars = sym('x', [1,numel(terms)]);
[cx, newvarsx] = coeffs(subs(f,terms,newvars), newvars);
tx = sym(zeros(1,numel(cx)));
for k=1:numel(newvarsx)
    if newvarsx(k) ~= 1
        tx(k) = terms(newvars == newvarsx(k));
    else
        tx(k) = newvarsx(k);
    end
end
cx = simplify(cx);

テーブル T を使って係数を表示します。cosFreqs を行識別子として使用します。

cosFreqs = arrayfun(@char,cosFreqs,'UniformOutput',false);
Frequencies = arrayfun(@char,freqs,'UniformOutput',false);
Coefficients = num2cell(zeros(size(freqs)));
T = table(Frequencies,Coefficients,'RowNames',cosFreqs);

tx の余弦項に対応する T の適切な行に cx を代入します。

nonzeroCosFreqs = arrayfun(@char,tx,'UniformOutput',false).';
T(nonzeroCosFreqs,'Coefficients') = arrayfun(@char,cx,'UniformOutput',false).';

ここで、不要な行名を削除します。

T.Properties.RowNames = {};

項に対応する式が LO と RF で対称であることを確認します。

T=25×2 table
      Frequencies                      Coefficients                 
    _______________    _____________________________________________

    {'0'          }    {'(Is*(c1^2 + c2^2))/(4*Vo^2)'              }
    {'RF'         }    {'(Is*c2*(8*Vo^2 + 2*c1^2 + c2^2))/(8*Vo^3)'}
    {'2*RF'       }    {'(Is*c2^2)/(4*Vo^2)'                       }
    {'3*RF'       }    {'(Is*c2^3)/(24*Vo^3)'                      }
    {'LO - 3*RF'  }    {[                                        0]}
    {'LO - 2*RF'  }    {'(Is*c1*c2^2)/(8*Vo^3)'                    }
    {'LO - RF'    }    {'(Is*c1*c2)/(2*Vo^2)'                      }
    {'LO'         }    {'(Is*c1*(8*Vo^2 + c1^2 + 2*c2^2))/(8*Vo^3)'}
    {'LO + RF'    }    {'(Is*c1*c2)/(2*Vo^2)'                      }
    {'LO + 2*RF'  }    {'(Is*c1*c2^2)/(8*Vo^3)'                    }
    {'LO + 3*RF'  }    {[                                        0]}
    {'2*LO - 3*RF'}    {[                                        0]}
    {'2*LO - 2*RF'}    {[                                        0]}
    {'2*LO - RF'  }    {'(Is*c1^2*c2)/(8*Vo^3)'                    }
    {'2*LO'       }    {'(Is*c1^2)/(4*Vo^2)'                       }
    {'2*LO + RF'  }    {'(Is*c1^2*c2)/(8*Vo^3)'                    }
      ⋮

係数の検証

以下に示すように、出力波形が係数から再構成され、出力と完全に一致しています。

simplify(f0 - (dot(tx,cx)))

ans =  $0$

非線形伝達関数のプロット

以下に、周波数と電圧比の特定の値について時間領域と周波数領域で上記のように解析した特定の非線形伝達関数を示します。まず、データを抽出します。

sample_values = struct('c1',0.4,'c2',1,'LO',800,'RF',13600,'Vo',1,'Is',1);
sample_input = subs(input,sample_values)

sample_input = 
 $\frac{2 \cos (800 t)}{5} + \cos (13600 t)$

sample_output = subs(f,sample_values)

sample_output = 
 $\frac{127 \cos (800 t)}{250} + \frac{\cos (1600 t)}{25} + \frac{\cos (2400 t)}{375} + \frac{\cos (12000 t)}{50} + \frac{\cos (12800 t)}{5} + \frac{233 \cos (13600 t)}{200} + \frac{\cos (14400 t)}{5} + \frac{\cos (15200 t)}{50} + \frac{\cos (26400 t)}{20} + \frac{\cos (27200 t)}{4} + \frac{\cos (28000 t)}{20} + \frac{\cos (40800 t)}{24} + \frac{29}{100}$

sample_freqs = zeros(size(tx));
for k=1:numel(tx)
    cosTerm = subs(tx(k),sample_values);
    freq = simplify(acos(cosTerm),'IgnoreAnalyticConstraints',true)/t;
    sample_freqs(k) = double(freq);
end
sample_heights = double(subs(cx,sample_values));

次に、fplot と stem を使って、関数とその高調波周波数をプロットします。

subplot(2,2,1);
fplot(sample_input,[0,0.01])
title Input
subplot(2,2,3);
stem([sample_values.LO, sample_values.RF],[sample_values.c1,sample_values.c2]);
title 'Input Frequencies'

subplot(2,2,2);
fplot(sample_output,[0,0.01])
title Output
subplot(2,2,4);
stem(sample_freqs,sample_heights)
title 'Output Frequencies'

Figure contains 4 axes objects. Axes object 1 with title Input contains an object of type functionline. Axes object 2 with title Input Frequencies contains an object of type stem. Axes object 3 with title Output contains an object of type functionline. Axes object 4 with title Output Frequencies contains an object of type stem.