Simulink でシンボリックに導出したプラントモデルのモデルパラメーターの推定

この例では次を使用します。

この例では Simulink Design Optimization™ を使用して、単純な抵抗コンデンサ (RC) 回路のシンボリックに導出した代数モデルの未知の静電容量と初期電圧を推定します。この例では同じ問題を解き、Estimate Model Parameters and Initial States (Code) (Simulink Design Optimization)と同じ実験データを使用しますが、RC 回路に微分形式ではなく閉形式の解を使用します。

この例では Symbolic Math Toolbox™ 機能を使用して、次を行います。

dsolve を使用して常微分方程式 (ODE) を解く
matlabFunctionBlockを使用して解析結果を Simulink® ブロックに変換する

設計の最適化を実行して解析 RC 回路の静電容量および初期電圧値を推定します。特に、実験出力電圧値をシミュレーションされた値と一致させます。

RC 回路の方程式の解法

以下の RC 回路の微分方程式を定義して解きます。

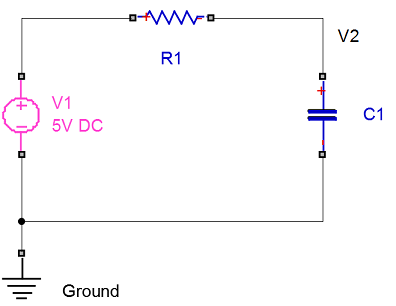
ここで、v2(t) はコンデンサ C1 にかかる出力電圧、v1 は抵抗 R1 にかかる定電圧、v20 はコンデンサにかかる初期電圧です。dsolve を使用して方程式を解きます。

syms C1 R1 v1 v20 real 
syms v2(t)
deq = (v1 - v2)/R1 - C1*diff(v2,t);
v2sol = dsolve(deq, v2(0) == v20)

v2sol = 
 $v_{1} - e^{- \frac{t}{C_{1} R_{1}}} (v_{1} - v_{20})$

subs を使用して 10 kOhm の R1 値と 5 V の v1 値の解を評価します。

v2sol = vpa(subs(v2sol,[R1,v1],[10e3,5]))

v2sol = 
 $e^{- \frac{0.0001 t}{C_{1}}} (v_{20} - 5.0) + 5.0$

RC 回路を表すブロックを使用したモデルの作成

まず、新規 Simulink モデルを作成します。

myModel = 'rcSymbolic';
new_system(myModel);
load_system(myModel);

matlabFunctionBlock を使用して出力電圧のシンボリックな結果を RC プラントモデルを表す Simulink ブロックに変換します。matlabFunctionBlock はこの新しいブロックをモデルに追加します。

blockName = 'closedFormRC_block';
rcBlock = strcat(myModel,'/',blockName);
myVars = [C1,v20,t];
matlabFunctionBlock(rcBlock,v2sol,...
    'vars',myVars,...
    'functionName','myRC',...
    'outputs',{'v2'});

より多くのブロックの追加

RC ブロックを基準とする位置とサイズでその他のブロックを追加および調整します。

rcBlockPosition = get_param(rcBlock,'position');
rcBlockWidth = rcBlockPosition(3)-rcBlockPosition(1);
rcBlockHeight = rcBlockPosition(4)-rcBlockPosition(2);
constantBlock = 'built-in/Constant';
timeBlock = 'simulink/Sources/Ramp';
outputBlock = 'built-in/Outport';

C1 および v20 は推定するパラメーターです。まず、460 $μ F$ および 1 V の初期値をそれぞれ使用し、MATLAB® ワークスペースでこれらのパラメーターを導入および初期化します。次に、両方のパラメーターに定数のブロックを作成します。

C1val = 460e-6;
v20val = 1.0;
posX = rcBlockPosition(1)-rcBlockWidth*2;
posY = rcBlockPosition(2)-rcBlockHeight*3/4;
pos = [posX,posY,posX+rcBlockWidth/2,posY+rcBlockHeight/2];
add_block(constantBlock,strcat(myModel,'/C1'),'Value','C1val',...
    'Position',pos);
pos = pos + [0 rcBlockHeight 0 rcBlockHeight];
add_block(constantBlock,strcat(myModel,'/v20'),'Value','v20val',...
    'Position',pos);

時間のランプを追加します。

pos = pos + [0 rcBlockHeight 0 rcBlockHeight];
add_block(timeBlock,strcat(myModel,'/t'),'Slope','1','Position',pos);

出力端子を追加します。

pos = [rcBlockPosition(1)+2*rcBlockWidth,...
    rcBlockPosition(2)+rcBlockHeight/4,...
    rcBlockPosition(1)+2*rcBlockWidth+rcBlockWidth/2,...
    rcBlockPosition(2)+rcBlockHeight/4+rcBlockHeight/2];
add_block(outputBlock,strcat(myModel,'/v2'),'Port','1','Position',pos);

次に、モデル内でブロックを結線します。Simulink Design Optimization に対するモデルの準備が整います。

myAddLine = @(k) add_line(myModel,...
    strcat(char(myVars(k)),'/1'),...
    strcat(blockName,'/',num2str(k)),...
    'autorouting','on');
arrayfun(myAddLine,(1:numel(myVars)));
add_line(myModel,strcat(blockName,'/1'),'v2/1','autorouting','on');
open_system(myModel);

パラメーターの推定

測定データを取得します。

load sdoRCCircuit_DataFromExperiment

変数 time および data がワークスペースに読み込まれます。data は時間 time に対して測定されたコンデンサ電圧です。

実験電圧データを保存する sdo.Experiment オブジェクトを作成します。

Exp = sdo.Experiment(myModel);

測定されたコンデンサ電圧出力を保存するオブジェクトを作成します。

Voltage = Simulink.SimulationData.Signal;
Voltage.Name      = 'Voltage';
Voltage.BlockPath = rcBlock;
Voltage.PortType  = 'outport';
Voltage.PortIndex = 1;
Voltage.Values    = timeseries(data,time);

測定されたコンデンサデータを予想される出力データとして実験に追加します。

Exp.OutputData = Voltage;

パラメーターを取得します。C1 の最小値を設定します。既に初期推定を指定していることに注意してください。

c1param = sdo.getParameterFromModel(myModel,'C1val');
c1param.Minimum = 0;
v20param = sdo.getParameterFromModel(myModel,'v20val');

推定の目的関数を定義します。この例で使用される sdoRCSymbolic_Objective のコードは、この例の最後の補助関数セクションで提供されます。

estFcn = @(v) sdoRCSymbolic_Objective(v,Exp,myModel);

推定するモデルパラメーターを収集します。

v = [c1param;v20param];

モデルは完全に代数なので、離散ソルバーを選択するように指示する警告メッセージをオフにします。

set_param(myModel,'SolverPrmCheckMsg','none');

パラメーターを推定します。

opt = sdo.OptimizeOptions;
opt.Method = 'lsqnonlin';
vOpt = sdo.optimize(estFcn,v,opt);

 Optimization started 2024-Mar-07, 18:00:39

                                          First-order 
 Iter F-count        f(x)      Step-size  optimality
    0      5      27.7093            1
    1     10      2.86889        1.919         2.94
    2     15      1.53851       0.3832        0.523
    3     20      1.35137       0.3347        0.505
    4     25      1.34473      0.01374      0.00842
    5     30      1.34472     0.002686      0.00141
Local minimum possible.

lsqnonlin stopped because the final change in the sum of squares relative to 
its initial value is less than the value of the function tolerance.

推定値を表示します。

fprintf('C1 = %e v20 = %e\n',vOpt(1).Value, vOpt(2).Value);

C1 = 2.261442e-04 v20 = 2.359446e+00

シミュレーションデータと実験データの比較

推定静電容量とコンデンサの初期電圧値を使用して実験を更新します。

Exp = setEstimatedValues(Exp,vOpt);

推定パラメーター値を使用してモデルをシミュレートし、シミュレーション出力と実験データを比較します。

Simulator = createSimulator(Exp);
Simulator = sim(Simulator);
SimLog    = find(Simulator.LoggedData,get_param(myModel,'SignalLoggingName'));
Voltage   = find(SimLog,'Voltage');
plot(time,data,'ro',Voltage.Values.Time,Voltage.Values.Data,'b')
title('Simulated and Measured Responses')
legend('Measured Voltage','Simulated Voltage','Location','Best')

close_system(myModel,0);

補助関数

function vals = sdoRCSymbolic_Objective(v,Exp,myModel) 
    r = sdo.requirements.SignalTracking;
    r.Type      = '==';
    r.Method    = 'Residuals';
    r.Normalize = 'off';
    Exp  = setEstimatedValues(Exp,v);
    Simulator = createSimulator(Exp);
    Simulator = sim(Simulator);
    SimLog  = find(Simulator.LoggedData,get_param(myModel,'SignalLoggingName'));
    Voltage = find(SimLog,'Voltage');
    VoltageError = evalRequirement(r,Voltage.Values,Exp.OutputData(1).Values);
    vals.F = VoltageError(:);
end

Simulink でシンボリックに導出したプラント モデルのモデル パラメーターの推定