cosh
シンボリック双曲線余弦関数
構文
説明
例
数値引数およびシンボリック引数に対する双曲線余弦関数
引数に応じて、cosh は浮動小数点解またはシンボリック厳密解の結果を返します。
次の数値について双曲線余弦関数を計算します。これらの数値はシンボリック オブジェクトではないため、cosh は浮動小数点の結果を返します。
A = cosh([-2, -pi*i, pi*i/6, 5*pi*i/7, 3*pi*i/2])
A =
3.7622 -1.0000 0.8660 -0.6235 -0.0000シンボリック オブジェクトに変換された数値に対する双曲線余弦関数を計算します。ほとんどのシンボリックな (厳密な) 数値に対して、cosh は未解決のシンボリックな呼び出しを返します。
symA = cosh(sym([-2, -pi*i, pi*i/6, 5*pi*i/7, 3*pi*i/2]))
symA = [ cosh(2), -1, 3^(1/2)/2, -cosh((pi*2i)/7), 0]
vpa を使用し、これらの解を浮動小数点数で近似します。
vpa(symA)
ans = [ 3.7621956910836314595622134777737,... -1.0,... 0.86602540378443864676372317075294,... -0.62348980185873353052500488400424,... 0]
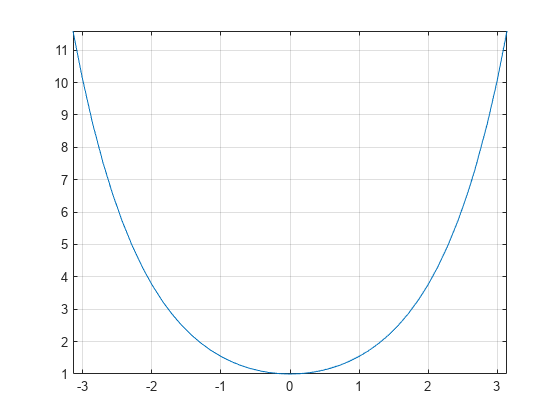
双曲線余弦関数のプロット
双曲線余弦関数を から までの範囲でプロットします。
syms x fplot(cosh(x),[-pi pi]) grid on
双曲線余弦関数を含む式の処理
diff、int、taylor および rewrite などの関数は cosh を含む式を処理することができます。
双曲線余弦関数の 1 次および 2 次導関数を求めます。
syms x diff(cosh(x), x) diff(cosh(x), x, x)
ans = sinh(x) ans = cosh(x)
双曲線余弦関数の不定積分を求めます。
int(cosh(x), x)
ans = sinh(x)
cosh(x) の式のテイラー級数展開を計算します。
taylor(cosh(x), x)
ans = x^4/24 + x^2/2 + 1
双曲線余弦関数を指数関数に書き換えます。
rewrite(cosh(x), 'exp')
ans = exp(-x)/2 + exp(x)/2
入力引数
バージョン履歴
R2006a より前に導入
