robustfit
ロバスト線形回帰の当てはめ
説明
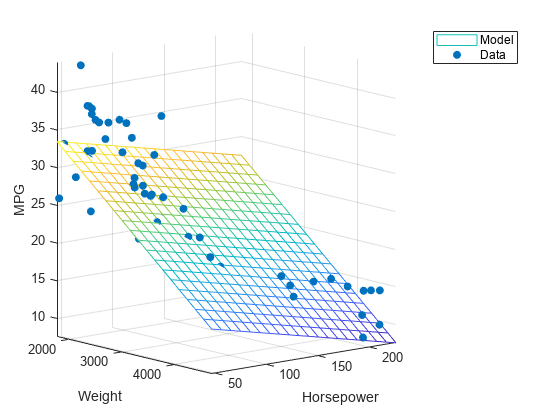
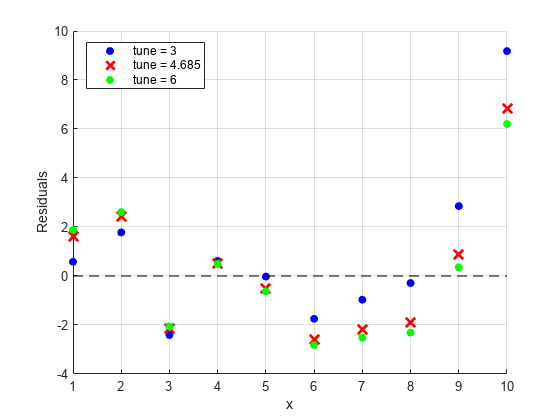
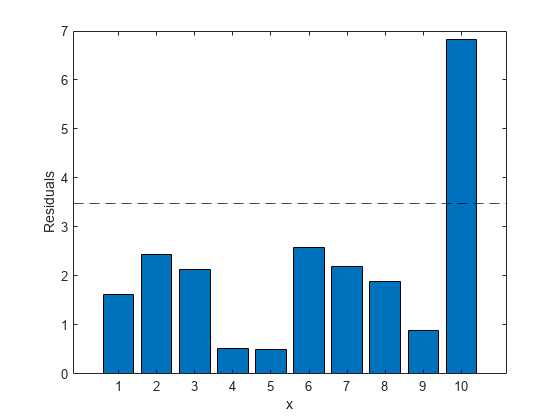
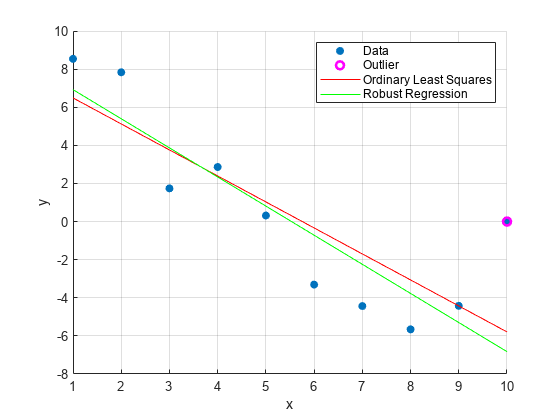
例
複数の線形モデルについて、ロバスト回帰係数を推定します。
carsmall データ セットを読み込みます。予測子として自動車の重量と馬力を、応答としてガロンあたりのマイル数による燃費を指定します。
load carsmall
x1 = Weight;
x2 = Horsepower;
X = [x1 x2];
y = MPG;ロバスト回帰係数を計算します。
b = robustfit(X,y)
b = 3×1
47.1975
-0.0068
-0.0333
近似モデルをプロットします。
x1fit = linspace(min(x1),max(x1),20); x2fit = linspace(min(x2),max(x2),20); [X1FIT,X2FIT] = meshgrid(x1fit,x2fit); YFIT = b(1) + b(2)*X1FIT + b(3)*X2FIT; mesh(X1FIT,X2FIT,YFIT)
データをプロットする。
hold on scatter3(x1,x2,y,'filled') hold off xlabel('Weight') ylabel('Horsepower') zlabel('MPG') legend('Model','Data') view(50,10) axis tight
異なる調整定数を使用して、ロバスト回帰の重み関数を調整します。
トレンド でデータを生成し、1 つの値を変更して外れ値をシミュレートします。
x = (1:10)'; rng ('default') % For reproducibility y = 10 - 2*x + randn(10,1); y(10) = 0;
3 つの異なる調整定数について、二重平方重み関数を使用してロバスト回帰残差を計算します。既定の調整定数は 4.685 です。
tune_const = [3 4.685 6]; for i = 1:length(tune_const) [~,stats] = robustfit(x,y,'bisquare',tune_const(i)); resids(:,i) = stats.resid; end
残差のプロットを作成します。
scatter(x,resids(:,1),'b','filled') hold on plot(resids(:,2),'rx','MarkerSize',10,'LineWidth',2) scatter(x,resids(:,3),'g','filled') plot([min(x) max(x)],[0 0],'--k') hold off grid on xlabel('x') ylabel('Residuals') legend('tune = 3','tune = 4.685','tune = 6','Location','best')
3 つの異なる調整定数について、残差の平方根平均二乗誤差 (RMSE) を計算します。
rmse = sqrt(mean(resids.^2))
rmse = 1×3
3.2577 2.7576 2.7099
調整定数を大きくすると、外れ値に割り当てられる重みの削減量が減るため、調整定数が大きくなるほど RMSE は小さくなります。
トレンド でデータを生成し、1 つの値を変更して外れ値をシミュレートします。
x = (1:10)'; rng('default') % For reproducibility y = 10 - 2*x + randn(10,1); y(10) = 0;
通常の最小二乗回帰を使用して直線を近似します。定数項があるモデルの係数推定値を計算するには、1 の列を x に含めます。
bls = regress(y,[ones(10,1) x])
bls = 2×1
7.8518
-1.3644
ロバスト回帰を使用して直線の近似を推定します。robustfit は、既定で定数項をモデルに追加します。
[brob,stats] = robustfit(x,y); brob
brob = 2×1
8.4504
-1.5278
残差と残差の中央絶対偏差を比較することにより、潜在的な外れ値を特定します。
outliers_ind = find(abs(stats.resid)>stats.mad_s);
ロバスト回帰の残差の棒グラフをプロットします。
bar(abs(stats.resid)) hold on yline(stats.mad_s,'k--') hold off xlabel('x') ylabel('Residuals')
データの散布図を作成します。
scatter(x,y,'filled')外れ値をプロットします。
hold on plot(x(outliers_ind),y(outliers_ind),'mo','LineWidth',2)
最小二乗とロバスト近似をプロットします。
plot(x,bls(1)+bls(2)*x,'r') plot(x,brob(1)+brob(2)*x,'g') hold off xlabel('x') ylabel('y') legend('Data','Outlier','Ordinary Least Squares','Robust Regression') grid on
ロバスト近似に対する外れ値の影響は、最小二乗近似よりも小さくなります。
入力引数
出力引数
詳細
アルゴリズム
robustfitは、反復的に再重み付けした最小二乗を使用して、係数bを計算します。入力wfunは重みを指定します。robustfitは、式inv(X'*X)*stats.s^2を使用して、係数推定値stats.covbの分散共分散行列を推定します。この推定により、標準誤差stats.seと相関stats.coeffcorrが生成されます。線形モデルにおいて、
yの観測値およびその残差は確率変数です。残差はゼロ平均を伴う正規分布ですが、予測子値によって分散が異なります。残差を比較可能なスケールにするため、robustfitは残差を "スチューデント化" します。つまりrobustfitは、残差の値に依存しない標準偏差の推定値で残差を除算します。スチューデント化残差は、既知の自由度をもつ t 分布に従います。robustfitは、stats.rstudのスチューデント化残差を返します。
代替機能
robustfit は、関数の出力引数のみが必要である場合、またはループ内でモデルの当てはめを複数回繰り返す場合に便利です。ロバストを当てはめた回帰モデルをさらに調べる必要がある場合は、fitlm を使用して線形回帰モデル オブジェクト LinearModel を作成します。名前と値のペアの引数 'RobustOpts' の値を 'on' に設定します。
参照
[1] DuMouchel, W. H., and F. L. O'Brien. “Integrating a Robust Option into a Multiple Regression Computing Environment.” Computer Science and Statistics: Proceedings of the 21st Symposium on the Interface. Alexandria, VA: American Statistical Association, 1989.
[2] Holland, P. W., and R. E. Welsch. “Robust Regression Using Iteratively Reweighted Least-Squares.” Communications in Statistics: Theory and Methods, A6, 1977, pp. 813–827.
[3] Huber, P. J. Robust Statistics. Hoboken, NJ: John Wiley & Sons, Inc., 1981.
[4] Street, J. O., R. J. Carroll, and D. Ruppert. “A Note on Computing Robust Regression Estimates via Iteratively Reweighted Least Squares.” The American Statistician. Vol. 42, 1988, pp. 152–154.
バージョン履歴
R2006a より前に導入
