ハット行列とてこ比

ハット行列

目的

ハット行列を使用するとてこ比を測定できます。これは、1 つ以上の観測値が X 値に関して外れ値となっていて、回帰結果に過剰な影響が発生していないかどうかを調べるのに便利です。

定義

ハット行列は "射影行列" とも呼ばれます。これは、観測値のベクトル y を予測値のベクトル $\hat{y}$ に射影するので "ハット" が y の上に置かれるためです。ハット行列 H は、データ行列 X に関して次のように定義されます。

H = X(X^TX)^–1X^T

また、次の式が成立するため、当てはめ値や予測値が決定されます。

$\hat{y} = H y = X b .$

H の対角要素 h_ii はてこ比と呼ばれ、次の条件を満たします。

$\begin{array}{l} 0 \leq h_{i i} \leq 1 \\ \sum_{i = 1}^{n} h_{i i} = p, \end{array}$

ここで、p は係数の数、n は回帰モデル内の観測 (X の行) の数です。HatMatrix はテーブル Diagnostics 内の n 行 n 列の行列です。

使用方法

近似モデル (mdl など) を取得した後、fitlm または stepwiselm を使用して、次のことを実行できます。

ドット表記でプロパティのインデックスを使用して、HatMatrix を表示する。
```
mdl.Diagnostics.HatMatrix
```
n が大きい場合、HatMatrix の計算量が増大する場合があります。そのような場合、次の方法で対角値を直接求めることができます。
```
mdl.Diagnostics.Leverage
```

てこ比

目的

てこ比は、入力空間で特定の観測の位置が原因で発生した、回帰予測におけるその観測値の影響を測定します。一般的に、入力空間の中心から離れた点ではてこ比が大きくなります。てこ比値の合計は p なので、てこ比値が平均てこ比値 p/n を大きく超えた値 (たとえば 2*p/n) である場合、観測 i は外れ値であると考えられます。

定義

観測値 i のてこ比は、ハット行列 H の i 番目の対角項 h_ii の値です。ここで

H = X(X^TX)^-1X^T

です。対角項は次の条件を満たしています。

$\begin{array}{l} 0 \leq h_{i i} \leq 1 \\ \sum_{i = 1}^{n} h_{i i} = p, \end{array}$

ここで、p は回帰モデルの係数の個数、n は観測値の個数です。定数項があるモデルでは、h_ii の最小値は 1/n です。近似モデルが原点を通過する場合、x = 0 の観測でてこ比の最小値は 0 になります。

次の関係が成立しているため、観測値 y を使用して近似値 $\hat{y}$ を表すことができます。

$\hat{y} = H y = X b .$

したがって、h_ii は ${\hat{y}}_{i}$ に対する観測値 y_i の影響の大きさを表します。h_ii の値が大きい場合、i 番目のケースがすべての n ケースの X 値の中心から離れており、てこ比も大きいことを示します。Leverage はテーブル Diagnostics の n 行 1 列のベクトルです。

使用方法

近似モデル (mdl など) を取得した後、fitlm または stepwiselm を使用して、次のことを実行できます。

ドット表記でプロパティのインデックスを使用して、Leverage ベクトルを表示する。
```
mdl.Diagnostics.Leverage
```
次の方法を使用して、モデルで近似された値のてこ比をプロットする。
```
plotDiagnostics(mdl)
```
詳細は、LinearModel クラスの plotDiagnostics メソッドを参照してください。

てこ比の高い観測値の特定

ライブスクリプトを開く

この例では、Leverage 値を計算し、てこ比の高い観測値を評価する方法を示します。標本データを読み込み、応答変数および独立変数を定義します。

load hospital
y = hospital.BloodPressure(:,1);
X = double(hospital(:,2:5));

線形回帰モデルを当てはめます。

mdl = fitlm(X,y);

てこ比値をプロットします。

plotDiagnostics(mdl)

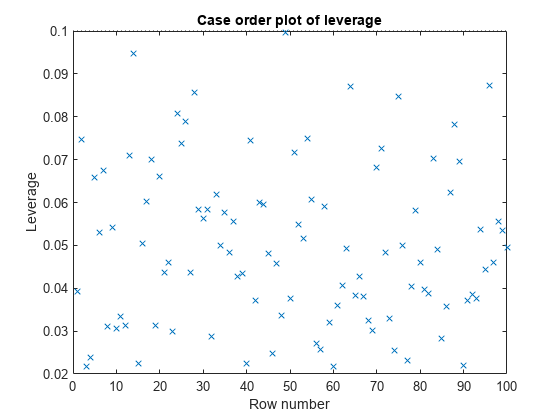
Figure contains an axes object. The axes object with title Case order plot of leverage, xlabel Row number, ylabel Leverage contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Leverage, Reference Line.