lof

異常検出用の局所外れ値因子モデルの作成

R2022b 以降

構文

LOFObj = lof(Tbl)

LOFObj = lof(X)

LOFObj = lof(___,Name=Value)

[LOFObj,tf] = lof(___)

[LOFObj,tf,scores] = lof(___)

説明

関数 lof は、外れ値の検出と新規性の検出のための局所外れ値因子モデルの作成に使用します。

• 外れ値検出 (学習データ中の異常を検出) — lof の出力引数 tf を使用して、学習データ中の異常を検出します。

• 新規性の検出 (汚染されていない学習データで新規のデータの異常を検出) — 汚染されていない学習データ (外れ値がないデータ) を lof に渡して LocalOutlierFactor オブジェクトを作成します。そのオブジェクトと新規データをオブジェクト関数 isanomaly に渡して、新規のデータの異常を検出します。

LOFObj = lof(Tbl) は、table Tbl の予測子データに対する LocalOutlierFactor オブジェクトを返します。

LOFObj = lof(X) は、行列 X の予測子データを使用します。

LOFObj = lof(___,Name=Value) では、前の構文におけるいずれかの入力引数の組み合わせに加えて、1 つ以上の名前と値の引数を使用してオプションを指定します。たとえば、ContaminationFraction=0.1 は、学習データの 10% を異常として処理するように関数に指示します。

[LOFObj,tf] = lof(___) は、Tbl または X の対応する行で異常が検出された場合に要素が true になる logical 配列 tf も返します。

[LOFObj,tf,scores] = lof(___) は、Tbl または X の各観測値についての異常スコア (局所外れ値因子の値) も返します。1 未満かそれに近いスコア値は正常な観測値を示し、1 より大きい値は異常の可能性を示します。

例

外れ値の検出

関数 lof を使用して、外れ値 (学習データ中の異常) を検出します。

標本データ セット NYCHousing2015 を読み込みます。

load NYCHousing2015

データ セットには、2015 年のニューヨーク市における不動産の売上に関する情報を持つ 10 の変数が含まれます。データ セットの概要を表示します。

summary(NYCHousing2015)

NYCHousing2015: 91446×10 table

Variables:

    BOROUGH: double
    NEIGHBORHOOD: cell array of character vectors
    BUILDINGCLASSCATEGORY: cell array of character vectors
    RESIDENTIALUNITS: double
    COMMERCIALUNITS: double
    LANDSQUAREFEET: double
    GROSSSQUAREFEET: double
    YEARBUILT: double
    SALEPRICE: double
    SALEDATE: datetime

Statistics for applicable variables:

                             NumMissing          Min              Median               Max               Mean               Std      

    BOROUGH                      0                     1                  3                  5             2.8431            1.3343  
    NEIGHBORHOOD                 0                                                                                                   
    BUILDINGCLASSCATEGORY        0                                                                                                   
    RESIDENTIALUNITS             0                     0                  1               8759             2.1789           32.2738  
    COMMERCIALUNITS              0                     0                  0                612             0.2201            3.2991  
    LANDSQUAREFEET               0                     0               1700           29305534         2.8752e+03        1.0118e+05  
    GROSSSQUAREFEET              0                     0               1056            8942176         4.6598e+03        4.3098e+04  
    YEARBUILT                    0                     0               1939               2016         1.7951e+03          526.9998  
    SALEPRICE                    0                     0             333333         4.1111e+09         1.2364e+06        2.0130e+07  
    SALEDATE                     0           01-Jan-2015        09-Jul-2015        31-Dec-2015        07-Jul-2015        2470:47:17  

NYCHousing2015 から非数値変数を削除します。変数 BOROUGH のデータ型は double ですが、これは不動産の所在地の区を示すカテゴリカル変数です。変数 BOROUGH も削除します。

NYCHousing2015 = NYCHousing2015(:,vartype("numeric"));
NYCHousing2015.BOROUGH = [];

NYCHousing2015 用に局所外れ値因子モデルに学習させます。学習観測値に含まれている異常の比率を 0.01 と指定します。

[Mdl,tf,scores] = lof(NYCHousing2015,ContaminationFraction=0.01);

Mdl は LocalOutlierFactor オブジェクトです。lof は、学習データ NYCHousing2015 の異常インジケーター (tf) および異常スコア (scores) も返します。

スコア値のヒストグラムをプロットします。指定した比率に対応するスコアのしきい値に垂直線を作成します。

h = histogram(scores,NumBins=50);
h.Parent.YScale = 'log';
xline(Mdl.ScoreThreshold,"r-",["Threshold" Mdl.ScoreThreshold]) 

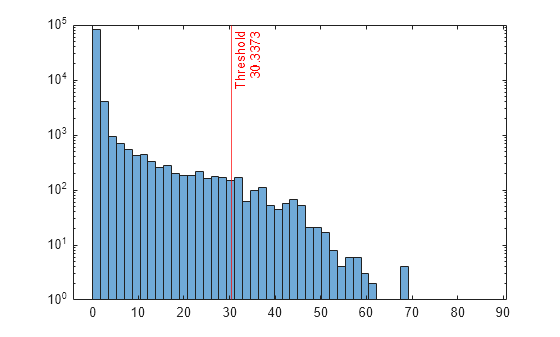
異なる汚染の比率 (たとえば 0.05) で異常を識別する場合は、新しい局所外れ値因子モデルに学習させることができます。

 [newMdl,newtf,scores] = lof(NYCHousing2015,ContaminationFraction=0.05);

汚染の比率を変更すると異常インジケーターのみが変更され、異常スコアは影響を受けないことに注意してください。したがって、lof を使用して異常スコアを再度計算しない場合、既存のスコア値で新しい異常インジケーターを取得できます。

学習データ中の異常の比率を 0.05 に変更します。

newContaminationFraction = 0.05;

関数quantileを使用して、新しいスコアのしきい値を求めます。

newScoreThreshold = quantile(scores,1-newContaminationFraction)

newScoreThreshold = 
6.7493

新しい異常インジケーターを取得します。

newtf = scores > newScoreThreshold;

新規性の検出

関数 lof を使用して、汚染されていない学習観測値用の LocalOutlierFactor オブジェクトを作成します。次に、オブジェクトおよび新規データをオブジェクト関数 isanomaly に渡して、新規性 (新規データ中の異常) を検出します。

census1994.mat に保存されている 1994 年の国勢調査データを読み込みます。このデータ セットは、個人の年収が $50,000 を超えるかどうかを予測するための、米国勢調査局の人口統計データから構成されます。

load census1994

census1994 には学習データ セット adultdata およびテスト データ セット adulttest が含まれています。LocalOutlierFactor オブジェクトに学習させるには、予測子データはすべて連続、またはすべて categorical のいずれかでなければなりません。adultdata および adulttest から非数値変数を削除します。

adultdata = adultdata(:,vartype("numeric"));
adulttest = adulttest(:,vartype("numeric"));

adultdata 用に局所外れ値因子モデルに学習させます。adultdata には外れ値が含まれていないと仮定します。

[Mdl,tf,s] = lof(adultdata);

Mdl は LocalOutlierFactor オブジェクトです。lof は、学習データ adultdata の異常インジケーター tf および異常スコア s も返します。名前と値の引数 ContaminationFraction を 0 を超える値として指定していない場合、lof はすべての学習観測値を正常な観測値として扱います。つまり tf の値はすべて logical 0 (false) となります。この関数によりスコアのしきい値が最大のスコア値に設定されます。しきい値を表示します。

Mdl.ScoreThreshold

ans = 
28.6719

学習済みの局所外れ値因子モデルを使用して、adulttest 内の異常を見つけます。

[tf_test,s_test] = isanomaly(Mdl,adulttest);

関数 isanomaly は、adulttest の異常インジケーター tf_test およびスコア s_test を返します。既定では、isanomaly はしきい値 (Mdl.ScoreThreshold) を超えるスコアをもつ観測値を異常として識別します。

異常スコア s および s_test のヒストグラムを作成します。異常スコアのしきい値に垂直線を作成します。

h1 = histogram(s,NumBins=50,Normalization="probability");
hold on
h2 = histogram(s_test,h1.BinEdges,Normalization="probability");
xline(Mdl.ScoreThreshold,"r-",join(["Threshold" Mdl.ScoreThreshold]))
h1.Parent.YScale = 'log';
h2.Parent.YScale = 'log';
legend("Training Data","Test Data",Location="north")
hold off

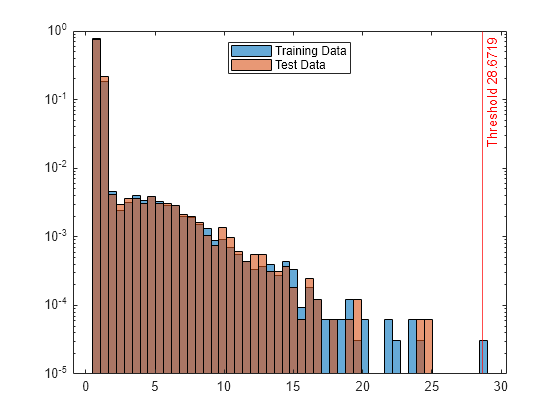
テスト データ中にある異常の観測値のインデックスを表示します。

find(tf_test)

ans =

  0×1 empty double column vector

テスト データの異常スコア分布は学習データの異常スコア分布と類似しているため、isanomaly は既定のしきい値でテスト データ中にある異常を検出しません。名前と値のペア ScoreThreshold を使用して、異なるしきい値を指定できます。例については、異常スコアのしきい値の指定を参照してください。

入力引数

Tbl — 予測子データ

table

予測子データ。table として指定します。Tbl の各行は 1 つの観測値に、各列は 1 つの予測子変数に対応します。文字ベクトルの cell 配列ではない cell 配列と複数列の変数は使用できません。

予測子データは、すべて連続、またはすべて categorical のいずれかでなければなりません。Tbl を指定した場合、関数 lof は、その変数が logical ベクトル、順序付けのない categorical ベクトル、文字配列、string 配列または文字ベクトルの cell 配列のいずれかである場合に、変数を categorical であると見なします。Tbl に連続値と categorical 値の両方が含まれている場合、Tbl のすべての予測子を categorical として特定するには、CategoricalPredictors を "all" として指定する必要があります。

Tbl 内の変数のサブセットを使用するには、名前と値の引数 PredictorNames を使用して変数を指定します。

データ型: table

X — 予測子データ

数値行列

予測子データ。数値行列として指定します。X の各行は 1 つの観測値に、各列は 1 つの予測子変数に対応します。

予測子データは、すべて連続、またはすべて categorical のいずれかでなければなりません。X を指定した場合、関数 lof はすべての予測子が連続的であると見なします。X のすべての予測子を categorical として特定するには、CategoricalPredictors を "all" として指定します。

名前と値の引数 PredictorNames を使用して X 内の予測子変数に名前を割り当てることができます。

データ型: single | double

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

例: SearchMethod=exhaustive,Distance=minkowski は、ミンコフスキー距離を指定して網羅的探索アルゴリズムを使用します。

BucketSize — ノード内のデータ点の最大数

50 (既定値) | 正の整数値

Kd 木の葉ノードにおけるデータ点の最大数。正の整数値として指定します。この引数は、SearchMethod が "kdtree" である場合のみ有効です。

例: BucketSize=40

データ型: single | double

CacheSize — メガバイト単位のグラム行列のサイズ

1000 (既定値) | 正のスカラー | "maximal"

メガバイト単位のグラム行列のサイズ。正のスカラーまたは "maximal" として指定します。グラム行列の定義については、アルゴリズムを参照してください。関数 lof では、名前と値の引数 Distance が "fasteuclidean" の場合にグラム行列を使用できます。

CacheSize が "maximal" の場合、lof は MX 行 MX 列のサイズの中間行列全体に十分なメモリを割り当てようと試みます。ここで、MX は入力データ X または Tbl の行数です。CacheSize は、中間行列全体に対して十分な大きさである必要はありませんが、少なくとも MX 行 1 列のベクトルを保持する十分な大きさでなければなりません。そうでない場合、lof は "euclidean" 距離を使用します。

Distance が "fasteuclidean" の場合、CacheSize の値が大きすぎるか "maximal" であると、利用可能なメモリを超えるグラム行列の割り当てが lof で試行されることがあります。この場合、MATLAB^® はエラーを生成します。

例: CacheSize="maximal"

データ型: double | char | string

CategoricalPredictors — カテゴリカル予測子フラグ

[] | "all"

カテゴリカル予測子フラグ。次のいずれかを指定します。

• "all" — すべての予測子がカテゴリカルです。既定では、lof は名前と値の引数 Distance にハミング距離 ("hamming") を使用します。

• [] — カテゴリカル予測子はありません。つまり、すべての予測子が連続的 (数値) です。この場合、Distance の既定値は "euclidean" です。

lof の予測子データは、すべて連続、またはすべて categorical のいずれかでなければなりません。

• 予測子データが table (Tbl) 内にある場合、lof は、その変数が logical ベクトル、順序付けのない categorical ベクトル、文字配列、string 配列または文字ベクトルの cell 配列のいずれかである場合に、変数を categorical であると見なします。Tbl に連続値と categorical 値の両方が含まれている場合、Tbl のすべての予測子を categorical として特定するには、CategoricalPredictors を "all" として指定する必要があります。

• 予測子データが行列 (X) である場合、lof はすべての予測子が連続的であると見なします。X のすべての予測子を categorical として特定するには、CategoricalPredictors を "all" として指定します。

lof は、正の整数値を各カテゴリに割り当てることにより、カテゴリカル変数を数値変数として符号化します。カテゴリカル予測子を使用する場合、必ず適切な距離計量 (Distance) を使用するようにしてください。

例: CategoricalPredictors="all"

ContaminationFraction — 学習データ中の異常の比率

0 (既定値) | 範囲 [0,1] の数値スカラー

学習データに含まれている異常の比率。範囲 [0,1] の数値スカラーとして指定します。

• ContaminationFraction の値が 0 (既定) の場合、lof はすべての学習観測値を正常な観測値として扱い、スコアのしきい値 (LOFObj の ScoreThreshold プロパティの値) を scores の最大値に設定します。

• ContaminationFraction の値が範囲 (0,1] にある場合、lof は指定された比率の学習観測値が異常として検出されるようにしきい値を決定します。

例: ContaminationFraction=0.1

データ型: single | double

Cov — 共分散行列

スカラー値の正定値行列

共分散行列。関数によるマハラノビス距離の計算時の共分散行列を表すスカラー値の正定値行列として指定します。この引数は、Distance が "mahalanobis" である場合のみ有効です。

既定値は、関数によって重複する値および欠損値を含む行が除外された後の予測子データ (Tbl または X) から計算された共分散行列です。

データ型: single | double

Distance — 距離計量

文字ベクトル | string スカラー

距離計量。文字ベクトルまたは string スカラーを指定します。

• すべての予測子変数が連続 (数値) 変数である場合、次の距離計量のうちの 1 つを指定できます。

  値	説明
  "euclidean"	ユークリッド距離
  "fasteuclidean"	データ点における要素の数が 10 個を超える場合に通常は時間の短縮になるアルゴリズムを使用したユークリッド距離。アルゴリズムを参照してください。"fasteuclidean" は "exhaustive" SearchMethod にのみ適用されます。
  "mahalanobis"	マハラノビス距離 — 名前と値の引数 Cov を使用して、マハラノビス距離の共分散行列を指定できます。
  "minkowski"	ミンコフスキー距離 — 名前と値の引数 Exponent を使用して、ミンコフスキー距離の指数を指定できます。
  "chebychev"	チェビシェフ距離 (最大座標差)
  "cityblock"	市街地距離
  "correlation"	1 から、観測値間の標本相関を減算 (値の系列として処理)
  "cosine"	1 から、ベクトルとして扱われる観測間の夾角の余弦を減算
  "spearman"	1 から観測値間の標本スピアマン順位相関係数を減算 (値の系列として処理)

  メモ

  これらの距離計量のうちの 1 つをカテゴリカル予測子に対して指定している場合、ソフトウェアは、各カテゴリカル予測子を距離計算用の数値変数として扱います。各カテゴリは正の整数で表されます。Distance の値は学習済みモデルの CategoricalPredictors プロパティに影響しません。

• すべての予測子変数がカテゴリカル変数である場合、次の距離計量のうちの 1 つを指定できます。

  値	説明
  "hamming"	ハミング距離 (異なる座標の比率)
  "jaccard"	1 からジャカード係数 (異なる非ゼロ座標の比率) を減算

  メモ

  これらの距離計量のうちの 1 つを連続 (数値) 予測子に対して指定している場合、ソフトウェアは、各連続予測子を距離計算用のカテゴリカル変数として扱います。このオプションでは CategoricalPredictors の値は変更されません。

すべての予測子変数が連続変数であれば、既定値は "euclidean" です。すべての予測子変数がカテゴリカル変数であれば、既定値は "hamming" です。

Kd 木アルゴリズム (SearchMethod="kdtree") を使用する場合、Distance は "euclidean"、"cityblock"、"minkowski" または "chebychev" にする必要があります。

さまざまな距離計量の詳細については、距離計量を参照してください。

例: Distance="jaccard"

データ型: char | string

Exponent — ミンコフスキー距離指数

2 (既定値) | 正のスカラー値

ミンコフスキー距離指数。正のスカラー値として指定します。この引数は、Distance が "minkowski" である場合のみ有効です。

例: Exponent=3

データ型: single | double

IncludeTies — 同順位使用フラグ

false または 0 (既定値) | true または 1

k 番目に小さい距離値の近傍をすべて含めるかどうかを示す同順位使用フラグ。logical 0 (false) または 1 (true) を指定します。IncludeTies が true である場合、すべての近傍が含まれます。それ以外の場合、正確に k 個の近傍が含まれます。

例: IncludeTies=true

データ型: logical

NumNeighbors — 最近傍の個数

min(20,n-1) (n は予測子データに含まれている一意の行の数) (既定値) | 正の整数値

局所外れ値因子の値を計算するために探索する予測子データ (Tbl または X) 内の最近傍の個数。正の整数値を指定します。

既定値は min(20,n-1) です。n は予測子データに含まれている一意の行の数です。

例: NumNeighbors=3

データ型: single | double

PredictorNames — 予測子変数名

読み取り専用: 一意な名前の string 配列 | 一意な文字ベクトルの cell 配列

この プロパティ は読み取り専用です。

予測子変数名。一意な名前の string 配列または一意な文字ベクトルの cell 配列として指定します。PredictorNames の機能は、予測子データの提供方法によって決まります。

• Tbl を指定した場合、PredictorNames を使用して使用する予測子変数を指定できます。つまり、lof は、PredictorNames の予測子変数のみを使用します。

  • PredictorNames は Tbl.Properties.VariableNames のサブセットである必要があります。

  • 既定では、Tbl のすべての予測子変数の名前が PredictorNames に格納されます。

• X を指定した場合、PredictorNames を使用して X 内の予測子変数に名前を割り当てることができます。

  • PredictorNames 内の名前の順序は、X の列の順序に一致しなければなりません。つまり、PredictorNames{1} は X(:,1) の名前、PredictorNames{2} は X(:,2) の名前であり、他も同様です。また、size(X,2) と numel(PredictorNames) は等しくなければなりません。

  • 既定では PredictorNames は {"x1","x2",...} です。

データ型: string | cell

SearchMethod — 最近傍探索法

"kdtree" | "exhaustive"

最近傍探索法。"kdtree" または "exhaustive" を指定します。

• "kdtree" — この方法では、Kd 木アルゴリズムを使用して最近傍を探索します。このオプションは、距離計量 (Distance) が次のいずれかである場合に有効です。

  • "euclidean" — ユークリッド距離

  • "cityblock" — 市街地距離

  • "minkowski" — ミンコフスキー距離

  • "chebychev" — チェビシェフ距離

• "exhaustive" — この方法では、網羅的探索アルゴリズムを使用して最近傍を探索します。

  • 予測子データ (Tbl または X) の局所外れ値因子の値を計算する場合、関数 lof は、予測子データ内のすべての点から予測子データ内の各点までの距離の値を計算することにより、最近傍を探索します。

  • 関数 isanomaly を使用して新しいデータ Xnew の局所外れ値因子の値を計算する場合、この関数は、予測子データ (Tbl または X) 内のすべての点から Xnew 内の各点までの距離の値を計算することにより、最近傍を探索します。

予測子データの列数が 10 以下で、データがスパースではなく、距離計量 (Distance) が Kd 木アルゴリズムに対して有効である場合、既定値は "kdtree" です。それ以外の場合、既定値は "exhaustive" です。

出力引数

LOFObj — 学習済みの局所外れ値因子モデル

LocalOutlierFactor オブジェクト

学習済みの局所外れ値因子モデル。LocalOutlierFactor オブジェクトとして返されます。

オブジェクト関数 isanomaly で LOFObj を使用して、新規のデータの異常を見つけることができます。

tf — 異常インジケーター

logical 列ベクトル

異常インジケーター。logical 列ベクトルとして返されます。tf の要素は、Tbl または X の対応する行の観測値が異常であれば logical 1 (true)、それ以外の場合は logical 0 (false) になります。tf の長さは Tbl または X と同じです。

lof は、scores がしきい値 (LOFObj の ScoreThreshold プロパティの値) を超える観測値を異常として識別します。関数は、指定された比率 (名前と値の引数 ContaminationFraction) の学習観測値が異常として検出されるようにしきい値を決定します。

scores — 異常スコア (局所外れ値因子の値)

数値列ベクトル

異常スコア (局所外れ値因子の値)。非負の値の数値列ベクトルとして返されます。scores の長さは Tbl または X と同じで、scores の各要素に Tbl または X の対応する行の観測値に対する異常スコアが格納されます。1 未満かそれに近いスコア値は正常な観測値を示し、1 より大きい値は異常の可能性を示します。

詳細

ローカルの外れ値因子

局所外れ値因子 (LOF) アルゴリズムでは、周囲の近傍に対する観測値の相対的な密度に基づいて異常を検出します。

このアルゴリズムでは、観測値の k 最近傍を探索し、観測値とその近傍の局所到達可能性密度を計算します。局所外れ値因子は、観測値とその近傍の平均密度比です。つまり、観測値 p の局所外れ値因子は次のようになります。

$$LO{F}_k(p)=\frac{1}{\left|N_k(p)\right|}{\displaystyle \sum _{o\in N_k(p)}\frac{lr{d}_k(o)}{lr{d}_k(p)}},$$

ここで

• lrd_k(·) は、観測値の局所到達可能性密度です。

• N_k(p) は、観測値 p の k 最近傍を表します。名前と値の引数 IncludeTies を true に指定して k 番目に小さい距離値の近傍をすべて含めるか、false に指定して正確に k 個の近傍を含めることができます。効率性能を高めるため、lof の IncludeTies の既定値は false です。[1]のアルゴリズムではすべての近傍が使用されることに注意してください。

• |N_k(p)| は N_k(p) 内の観測値数です。

正常な観測値の場合、局所外れ値因子の値は 1 未満かそれに近い値で、観測値の局所到達可能性密度がその近傍より高いか同等であることを示します。局所外れ値因子の値が 1 より大きい場合は、異常の可能性を示します。局所外れ値因子の値のしきい値は、lof の ContaminationFraction 引数と isanomaly の ScoreThreshold 引数で制御します。

このアルゴリズムでは、到達可能性距離に基づいて密度を測定します。観測値 o に対する観測値 p の到達可能性距離は次のように定義されます。

$${\tilde{d}}_k(p,o)=\max (d_k(o),d(p,o)),$$

ここで

• d_k(o) は、観測値 o からその近傍までの距離の中で k 番目に短い距離です。

• d(p,o) は、観測値 p と観測値 o の間の距離です。

このアルゴリズムでは、到達可能性距離を使用して、観測値 o に近い観測値の d(p,o) の統計変動を低減します。

観測値 p の局所到達可能性密度は、観測値 p からその近傍までの平均到達可能性距離の逆数です。

$$lr{d}_k(p)=1/\frac{{\displaystyle \sum _{o\in N_k(p)}{\tilde{d}}_k(p,o)}}{\left|N_k(p)\right|}.$$

重複の数が近傍の数 (k) より大きい場合、密度値は無限大になる可能性があります。そのため、学習データに重複が含まれている場合、関数 lof と関数 isanomaly では加重局所外れ値因子 (WLOF) アルゴリズムが使用されます。このアルゴリズムでは、加重局所到達可能性密度 (wlrd) を使用して加重局所外れ値因子を計算します。

$$WLO{F}_k(p)=\frac{1}{{\displaystyle \sum _{o\in N_k(p)}w(o)}}{\displaystyle \sum _{o\in N_k(p)}\frac{wlr{d}_k(o)}{wlr{d}_k(p)}},$$

ここで

$$wlr{d}_k(p)=1/\frac{{\displaystyle \sum _{o\in N_k(p)}w(o){\tilde{d}}_k(p,o)}}{{\displaystyle \sum _{o\in N_k(p)}w(o)}},$$

w(o) は、学習データに含まれている観測値 o の重複の数です。重みの値を計算した後、このアルゴリズムでは重複の各セットが 1 つの観測値として扱われます。

距離計量

距離計量は、2 つの観測値の間の距離を定義する関数です。lof は、連続変数とカテゴリカル変数用のさまざまな距離計量をサポートします。

mx 行 n 列のデータ行列 X (mx 個の 1 行 n 列の行ベクトル x₁、x₂、...、x_mx として扱われる) と、my 行 n 列のデータ行列 Y (my 個の 1 行 n 列の行ベクトル y₁、y₂、...、y_my として扱われる) が与えられた場合、ベクトル x_s と y_t の間のさまざまな距離は次のように定義されます。

• 連続 (数値) 変数の距離計量

  • ユークリッド距離

    $$d_{st}^2=(x_s-y_t)(x_s-y_t{)}^{\prime }.$$

    ユークリッド距離はミンコフスキー距離の特殊なケース、p = 2 の場合です。

  • 高速ユークリッド距離はユークリッド距離と同じですが、観測値 n における変数の数が 10 個を超える場合に通常は時間の短縮になるアルゴリズムを使用します。アルゴリズムを参照してください。

  • マハラノビス距離

    $$d_{st}^2=(x_s-y_t)C^{-1}(x_s-y_t{)}^{\prime },$$

    ここで、C は共分散行列です。

  • 市街地距離

    $$d_{st}={\displaystyle \sum _{j=1}^n\left|x_{sj}-y_{tj}\right|}.$$

    市街地距離はミンコフスキー距離の特殊なケース、p = 1 の場合です。

  • ミンコフスキー距離

    $$d_{st}=\sqrt[p]{{\displaystyle \sum _{j=1}^n{\left|x_{sj}-y_{tj}\right|}^p}}.$$

    p = 1 という特殊なケースでは、ミンコフスキー距離は市街地距離を与えます。p = 2 という特殊なケースでは、ミンコフスキー距離はユークリッド距離を与えます。p = ∞ という特殊なケースでは、ミンコフスキー距離はチェビシェフ距離を与えます。

  • チェビシェフ距離

    $$d_{st}={\max }_j\left\{\left|x_{sj}-y_{tj}\right|\right\}.$$

    チェビシェフ距離はミンコフスキー距離の特殊なケース、p = ∞ の場合です。

  • コサイン距離

    $$d_{st}=\left(1-\frac{x_s{y^{\prime }}_t}{\sqrt{\left(x_s{x^{\prime }}_s\right)\left(y_t{y^{\prime }}_t\right)}}\right).$$

  • 相関距離

    $$d_{st}=1-\frac{\left(x_s-{\overline{x}}_s\right){\left(y_t-{\overline{y}}_t\right)}^{\prime }}{\sqrt{\left(x_s-{\overline{x}}_s\right){\left(x_s-{\overline{x}}_s\right)}^{\prime }}\sqrt{\left(y_t-{\overline{y}}_t\right){\left(y_t-{\overline{y}}_t\right)}^{\prime }}},$$

    ここで

    $${\overline{x}}_s=\frac{1}{n}{\displaystyle \sum _j{x}_{sj}}$$

    および

    $${\overline{y}}_t=\frac{1}{n}{\displaystyle \sum _j{y}_{tj}}.$$

  • スピアマン距離は、1 から一連の値として扱われる観測値間の標本スピアマン順位相関係数を引きます。

    $$d_{st}=1-\frac{\left(r_s-{\overline{r}}_s\right){\left(r_t-{\overline{r}}_t\right)}^{\prime }}{\sqrt{\left(r_s-{\overline{r}}_s\right){\left(r_s-{\overline{r}}_s\right)}^{\prime }}\sqrt{\left(r_t-{\overline{r}}_t\right){\left(r_t-{\overline{r}}_t\right)}^{\prime }}},$$

    ここで

    • r_sj は、tiedrank により計算される、x_1j、x_2j、...x_mx,j から取得された x_sj の順位です。

    • r_tj は、tiedrank により計算される、y_1j、y_2j、...y_my,j から取得された y_tj の順位です。

    • r_s および r_t は、x_s および y_t の座標単位の順位ベクトルです。つまり、r_s = (r_s1, r_s2, ... r_sn) および r_t = (r_t1, r_t2, ... r_tn) です。

    • $${\overline{r}}_s=\frac{1}{n}{\displaystyle \sum _j{r}_{sj}}=\frac{\left(n+1\right)}{2}$$.

    • $${\overline{r}}_t=\frac{1}{n}{\displaystyle \sum _j{r}_{tj}}=\frac{\left(n+1\right)}{2}$$.

• カテゴリカル変数の距離計量

  • ハミング距離

    $$d_{st}=(\#(x_{sj}\ne y_{tj})/n).$$

    ハミング距離は、一致しない座標の比率です。

  • Jaccard 距離は、1 からジャカード係数 (異なる非ゼロ座標の比率) を引きます。

    $$d_{st}=\frac{\#\left[\left(x_{sj}\ne y_{tj}\right)\cap \left(\left(x_{sj}\ne 0\right)\cup \left(y_{tj}\ne 0\right)\right)\right]}{\#\left[\left(x_{sj}\ne 0\right)\cup \left(y_{tj}\ne 0\right)\right]}.$$

アルゴリズム

欠損値

lof は、Tbl に含まれている NaN、'' (空の文字ベクトル)、"" (空の string)、<missing>、<undefined> の値と X に含まれている NaN 値を欠損値と見なします。

• lof は、欠損値のある観測値は使用しません。

• lof は、欠損値のある観測値に異常スコア NaN および異常インジケーター false (logical 0) を割り当てます。

高速ユークリッド距離アルゴリズム

"fasteuclidean" Distance では、計算時間の短縮のために追加のメモリを使用してユークリッド距離が計算されます。このアルゴリズムは、Albanie の[2]などで "ユークリッド距離行列トリック" として提唱されているものです。内部テストでは、このアルゴリズムによって予測子の数が 10 個を超える場合に時間の短縮になることが確認されています。"fasteuclidean" 距離ではスパース データはサポートされません。

このアルゴリズムでは、x_i と x_j のすべての点間の距離の行列 D を求めるために (x_i のそれぞれに n 個の変数を格納)、次の方程式の最後の行を使用して距離を計算します。

$$\begin{array}{c}{D}_{i,j}^2=\Vert x_i-x_j{\Vert }^2\\ ={(}^{x_i}(x_i-x_j)\\ =\Vert x_i{\Vert }^2-2x_i^T{x}_j+\Vert x_j{\Vert }^2.\end{array}$$

方程式の最後の行にある行列 $$x_i^T{x}_j$$ は "グラム行列" と呼ばれます。正方化と加算によって平方距離を計算する代わりに、グラム行列を計算して使用すると、一連の平方距離の計算は高速になりますが、数値的安定性は少し低くなります。詳細については、Albanie の[2]を参照してください。

グラム行列を格納するためにソフトウェアで既定で使用されるキャッシュのサイズは 1e3 メガバイトです。キャッシュ サイズは名前と値の引数 CacheSize を使用して設定できます。CacheSize の値が大きすぎるか "maximal" である場合、利用可能なメモリを超えるグラム行列の割り当てが lof で試行されることがあります。この場合、MATLAB はエラーを生成します。

参照

[1] Breunig, Markus M., et al. “LOF: Identifying Density-Based Local Outliers.” Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, 2000, pp. 93–104.

[2] Albanie, Samuel. Euclidean Distance Matrix Trick. June, 2019. Available at https://samuelalbanie.com/files/Euclidean_distance_trick.pdf.

バージョン履歴

R2022b で導入

R2023b: "fasteuclidean" 距離のサポート

関数 lof で "fasteuclidean" Distance アルゴリズムがサポートされます。このアルゴリズムにより、データ点における変数の数が 10 個を超える場合に、通常は既定の "euclidean" アルゴリズムよりも距離の計算が高速になります。このアルゴリズムでは中間グラム行列を格納するために追加のメモリが使用されます (アルゴリズムを参照)。このメモリ割り当てのサイズは名前と値の引数 CacheSize を使用して設定します。

参考

LocalOutlierFactor | isanomaly | iforest | rrcforest | ocsvm | robustcov

トピック

• 教師なし異常検出