fitsemigraph

グラフベースの半教師あり手法を使用したデータへのラベル付け

構文

Mdl = fitsemigraph(Tbl,ResponseVarName,UnlabeledTbl)

Mdl = fitsemigraph(Tbl,formula,UnlabeledTbl)

Mdl = fitsemigraph(Tbl,Y,UnlabeledTbl)

Mdl = fitsemigraph(X,Y,UnlabeledX)

Mdl = fitsemigraph(___,Name,Value)

説明

fitsemigraph は、ラベル付けされたデータ、ラベル、およびラベル付けされていないデータが与えられた、半教師ありグラフベース モデルを作成します。返されるモデルには、ラベル付けされていないデータに当てはめられたラベル、および対応するスコアが含まれます。このモデルは、オブジェクト関数 predict を使用して未観測データのラベルを予測することもできます。異なるラベル付けアルゴリズムの詳細については、アルゴリズムを参照してください。

Mdl = fitsemigraph(Tbl,ResponseVarName,UnlabeledTbl) は Tbl 内のラベル付けされたデータを使用します。ここで、Tbl.ResponseVarName はラベル付けされたデータのラベルを格納しており、UnlabeledTbl 内のラベル付けされていないデータに当てはめられたラベルを返します。この関数は、オブジェクト Mdl の FittedLabels プロパティおよび LabelScores プロパティに、当てはめられたラベルおよび対応するスコアをそれぞれ保存します。

Mdl = fitsemigraph(Tbl,formula,UnlabeledTbl) は、formula を使用して、Tbl に含まれる変数で使用する応答変数 (ラベルのベクトル) と予測子変数を指定します。この関数は、これらの変数を使用して、UnlabeledTbl 内のデータにラベルを付けます。

Mdl = fitsemigraph(Tbl,Y,UnlabeledTbl) は、Tbl 内の予測子データと Y 内のラベルを使用して、UnlabeledTbl 内のデータにラベルを付けます。

Mdl = fitsemigraph(X,Y,UnlabeledX) は、X 内の予測子データと Y 内のラベルを使用して、UnlabeledX 内のデータにラベルを付けます。

Mdl = fitsemigraph(___,Name,Value) では、前の構文におけるいずれかの入力引数の組み合わせに加えて、1 つ以上の名前と値のペアの引数を使用してオプションを指定します。たとえば、ラベル付けアルゴリズムで使用するラベル付けの方法、反復回数、およびスコアのしきい値を指定できます。

例

ラベル付けされていないデータへのラベルの当てはめ

グラフベースの半教師あり手法を使用して、ラベル付けされていないデータにラベルを当てはめます。

ラベル付けされたデータの観測値をランダムに 60 個生成し、その観測値が 20 個ずつ 3 つのクラスに属するようにします。

rng('default') % For reproducibility

labeledX = [randn(20,2)*0.25 + ones(20,2);
            randn(20,2)*0.25 - ones(20,2);
            randn(20,2)*0.5];
Y = [ones(20,1); ones(20,1)*2; ones(20,1)*3];

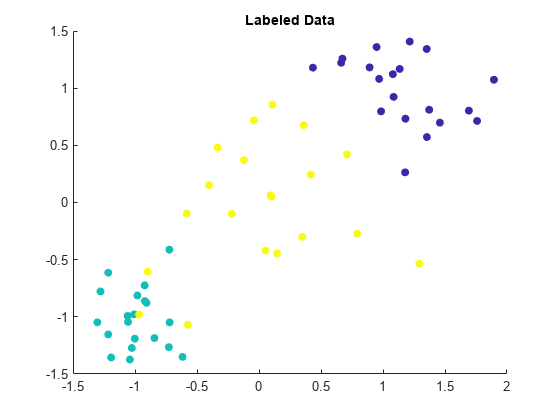
散布図を使用して、ラベル付けされたデータを可視化します。同じクラスに属する観測値は同じ色で示します。データは 3 つのクラスターに分割されていますが、わずかにオーバーラップしていることに注意してください。

scatter(labeledX(:,1),labeledX(:,2),[],Y,'filled')
title('Labeled Data')

ラベル付けされていないデータの観測値を追加でランダムに 300 個生成し、各クラスに 100 個ずつ属するようにします。検証のため、ラベル付けされていないデータの真のラベルを追跡します。

unlabeledX = [randn(100,2)*0.25 + ones(100,2);
              randn(100,2)*0.25 - ones(100,2);
              randn(100,2)*0.5];
trueLabels = [ones(100,1); ones(100,1)*2; ones(100,1)*3];

グラフベースの半教師あり手法を使用して、ラベル付けされていないデータにラベルを当てはめます。関数 fitsemigraph は SemiSupervisedGraphModel オブジェクトを返します。このオブジェクトの FittedLabels プロパティにはラベル付けされていないデータに当てはめられたラベルが、LabelScores プロパティには関連するラベル スコアが含まれます。

Mdl = fitsemigraph(labeledX,Y,unlabeledX)

Mdl = 
  SemiSupervisedGraphModel with properties:

             FittedLabels: [300×1 double]
              LabelScores: [300×3 double]
               ClassNames: [1 2 3]
             ResponseName: 'Y'
    CategoricalPredictors: []
                   Method: 'labelpropagation'


  Properties, Methods

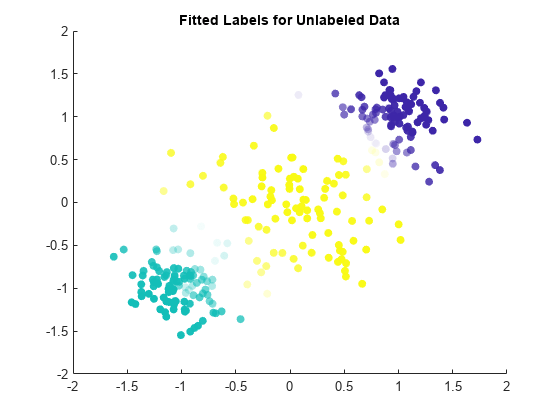
散布図を使用して、当てはめられたラベルの結果を可視化します。当てはめられたラベルを使用して観測値の色を設定し、最大のラベル スコアを使用して観測値の透明度を設定します。透明度が低い観測値には、高い信頼度のラベルを付けます。クラスターの境界付近に位置している観測値には、低い信頼度のラベルが付いていることに注意してください。

maxLabelScores = max(Mdl.LabelScores,[],2);
rescaledScores = rescale(maxLabelScores,0.05,0.95);
scatter(unlabeledX(:,1),unlabeledX(:,2),[],Mdl.FittedLabels,'filled', ...
    'MarkerFaceAlpha','flat','AlphaData',rescaledScores);
title('Fitted Labels for Unlabeled Data')

ラベル付けされていないデータの真のラベルを使用して、ラベル付けの精度を判断します。

numWrongLabels = sum(trueLabels ~= Mdl.FittedLabels)

numWrongLabels = 
10

unlabeledX 内の 300 個の観測値のうち、誤ったラベルが付けられた観測値はわずか 10 個です。

ラベルの当てはめに使用するグラフのタイプの指定

グラフベースの半教師あり手法を使用して、ラベル付けされていないデータにラベルを当てはめます。最近傍グラフのタイプを指定します。

patients データ セットを読み込みます。変数 Distolic、Gender などから table を作成します。各観測値、つまり table の行では、Smoker 値をその観測値のラベルとして扱います。

load patients
Tbl = table(Diastolic,Gender,Height,Systolic,Weight,Smoker);

観測値の 20% にのみラベルが付けられているものとします。このシナリオを再作成するために、ラベル付けされた観測値を 20 個無作為に抽出し、それを table unlabeledTbl に保存します。残りの観測値からラベルを削除し、それを table unlabeledTbl に保存します。例の終わりでラベルの当てはめの精度を確認するため、ラベル付けされていないデータの真のラベルを変数 trueLabels に保持します。

rng('default') % For reproducibility of the sampling
[labeledTbl,Idx] = datasample(Tbl,20,'Replace',false);

unlabeledTbl = Tbl;
unlabeledTbl(Idx,:) = [];
trueLabels = unlabeledTbl.Smoker;
unlabeledTbl.Smoker = [];

グラフベースの半教師あり手法を使用して、ラベル付けされていないデータにラベルを当てはめます。相互型の最近傍グラフを使用します。このグラフでは、互いに最近傍である 2 点が接続されます。数値予測子を標準化するための指定を行います。関数 fitsemigraph が返すオブジェクトの FittedLabels プロパティには、ラベル付けされていないデータに当てはめられたラベルが含まれます。

Mdl = fitsemigraph(labeledTbl,'Smoker',unlabeledTbl,'KNNGraphType','mutual', ...
    'Standardize',true);
fittedLabels = Mdl.FittedLabels;

誤ってラベルが付けられた観測値を特定するため、保存済みのラベル付けされていないデータの真のラベルを、グラフベースの半教師あり手法で返された当てはめ済みのラベルと比較します。

wrongIdx = (trueLabels ~= fittedLabels);
wrongTbl = unlabeledTbl(wrongIdx,:);

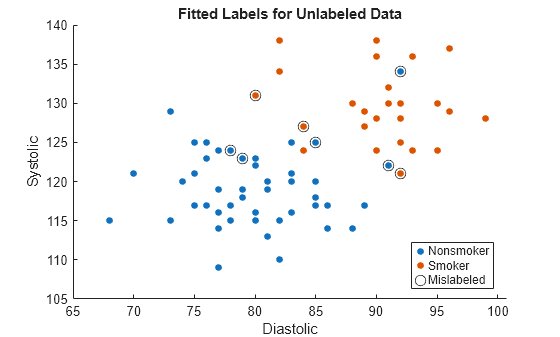
ラベル付けされていないデータに当てはめられたラベルの結果を可視化します。誤ってラベルが付けられた観測値は、プロット内で円で囲まれます。

gscatter(unlabeledTbl.Diastolic,unlabeledTbl.Systolic, ...
    fittedLabels)
hold on
plot(wrongTbl.Diastolic,wrongTbl.Systolic, ...
    'ko','MarkerSize',8)
xlabel('Diastolic')
ylabel('Systolic')
legend('Nonsmoker','Smoker','Mislabeled')
title('Fitted Labels for Unlabeled Data')

入力引数

Tbl — ラベル付けされた標本データ

table

ラベル付けされた標本データ。table として指定します。Tbl の各行は 1 つの観測値に、各列は 1 つの予測子に対応します。オプションで、Tbl に応答変数 (ラベルのベクトル) 用の列を 1 つ追加できます。複数列の変数、文字ベクトルの cell 配列ではない cell 配列、および順序カテゴリカル変数はサポートされません。

Tbl に応答変数が含まれている場合に Tbl 内の他の変数をすべて予測子として使用するには、ResponseVarName を使用して応答変数を指定します。

Tbl に応答変数が含まれている場合に Tbl 内の他の変数の一部のみを予測子として使用するには、formula を使用して式を指定します。

Tbl に応答変数が含まれていない場合は、Y を使用して応答変数を指定します。応答変数の長さと Tbl の行数は等しくなければなりません。

データ型: table

UnlabeledTbl — ラベル付けされていない標本データ

table

ラベル付けされていない標本データ。table として指定します。UnlabeledTbl の各行は 1 つの観測値に、各列は 1 つの予測子に対応します。UnlabeledTbl には、Tbl に含まれるものと同じ予測子が含まれなければなりません。

データ型: table

ResponseVarName — 応答変数名

Tbl 内の変数の名前

応答変数の名前。Tbl 内の変数の名前で指定します。この応答変数には、Tbl 内の標本データのクラス ラベルが含まれます。

ResponseVarName には文字ベクトルまたは string スカラーを指定しなければなりません。たとえば、応答変数 Y が Tbl.Y として格納されている場合、'Y' として指定します。それ以外の場合、Tbl の列は Y を含めてすべて予測子として扱われます。

応答変数は、categorical 配列、文字配列、string 配列、logical ベクトル、数値ベクトル、または文字ベクトルの cell 配列でなければなりません。Y が文字配列である場合、応答変数の各要素は配列の 1 つの行に対応しなければなりません。

名前と値のペアの引数 ClassNames を使用してクラスの順序を指定することをお勧めします。

データ型: char | string

formula — 応答変数および予測子変数サブセットの説明モデル

文字ベクトル | string スカラー

応答変数および予測子変数サブセットの説明モデル。'Y~X1+X2+X3' という形式の文字ベクトルまたは string スカラーを指定します。この式では、Y は応答変数を、X1、X2 および X3 は予測子変数を表します。

予測子として Tbl 内の変数のサブセットを指定するには、式を使用します。式を指定した場合、formula に現れない Tbl 内の変数は使用されません。

式の変数名は Tbl の変数名 (Tbl.Properties.VariableNames) であり、有効な MATLAB^® 識別子でなければなりません。関数 isvarname を使用して Tbl の変数名を検証できます。変数名が有効でない場合、関数 matlab.lang.makeValidName を使用してそれらを変換できます。

データ型: char | string

Y — クラス ラベル

数値ベクトル | categorical ベクトル | logical ベクトル | 文字配列 | string 配列 | 文字ベクトルの cell 配列

クラス ラベル。数値ベクトル、categorical ベクトル、logical ベクトル、文字配列、string 配列、または文字ベクトルの cell 配列として指定します。

• Y が文字配列である場合、クラス ラベルの各要素は配列の 1 つの行に対応しなければなりません。

• Y の長さは Tbl または X の行数と等しくなければなりません。

• 名前と値のペアの引数 ClassNames を使用してクラスの順序を指定することをお勧めします。

データ型: single | double | categorical | logical | char | string | cell

X — ラベル付けされた予測子データ

数値行列

ラベル付けされた予測子データ。数値行列として指定します。

X の各行は 1 つの観測値に、各列は 1 つの予測子に対応します。

Y の長さと X の行数は等しくなければなりません。

予測子の名前を X に表示される順序で指定するには、PredictorNames 名前と値のペアの引数を使用します。

データ型: single | double

UnlabeledX — ラベル付けされていない予測子データ

数値行列

ラベル付けされていない予測子データ。数値行列として指定します。UnlabeledX の各行は 1 つの観測値に、各列は 1 つの予測子に対応します。UnlabeledX は、X と同じ予測子を同じ順序で格納していなければなりません。

データ型: single | double

メモ

NaN、空の文字ベクトル ('')、空の string ("")、<missing> および <undefined> 要素は欠損データとして扱われます。ソフトウェアは、欠損値のある予測子データ (観測値) の行を削除します。

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。

例: fitsemigraph(Tbl,'Y',UnlabeledTbl,'Method','labelspreading','IterationLimit',2e3) は、ラベル拡散によるラベル付けの手法を使用すること、および反復の最大実行回数を 2000 回とすることを指定します。

ラベル付けアルゴリズム オプション

Method — ラベル付けの手法

'labelpropagation' (既定値) | 'labelpropagationexact' | 'labelspreading' | 'labelspreadingexact'

ラベル付けの手法。'Method' と次のいずれかの値で構成されるコンマ区切りのペアとして指定します。

値	説明	方法に固有の名前と値のペアの引数
'labelpropagation'	類似度グラフ内のノードにラベルを反復的に伝播します。詳細は、ラベル伝播を参照してください。	'IterationLimit' — 最大反復回数 'Tolerance' — 以後の反復におけるスコア差の絶対値に対する許容誤差
'labelpropagationexact'	正確な式を使用してラベルを伝播します。詳細は、ラベル伝播を参照してください。	なし
'labelspreading'	類似度グラフ内のノードにラベルを反復的に拡散します。詳細は、ラベル拡散を参照してください。	'Alpha' — 初期ラベルに対する隣接ラベルの相対的な重み 'IterationLimit' — 最大反復回数 'Tolerance' — 以後の反復におけるスコア差の絶対値に対する許容誤差
'labelspreadingexact'	正確な式を使用してラベルを拡散します。詳細は、ラベル拡散を参照してください。	'Alpha' — 初期ラベルに対する隣接ラベルの相対的な重み

例: 'Method','labelspreading'

データ型: char | string

Alpha — 初期ラベルに対する隣接ラベルの相対的な重み

0.01 (既定値) | (0,1) の範囲のスカラー値

X または Tbl に含まれるラベル付けされた観測値の初期ラベルに対する、隣接ラベルの相対的な重み。'Alpha' と (0,1) の範囲にあるスカラー値で構成されるコンマ区切りのペアとして指定します。値が 0 に近い場合、fitsemigraph が初期にラベル付けされた観測値のラベルをグラウンド トゥルースのように扱うことを示します。値が 1 に近い場合、fitsemigraph が初期にラベル付けされた観測値のラベルをノイズのように扱うことを示します。

メモ

この引数は、Method 値が 'labelspreading' または 'labelspreadingexact' である場合のみ有効です。

例: 'Alpha',0.05

データ型: single | double

IterationLimit — 最大反復回数

1e3 (既定値) | 正の整数スカラー

最大反復回数。'IterationLimit' と正の整数スカラーで構成されるコンマ区切りのペアとして指定します。この上限に到達した場合、アルゴリズムが収束しなくても、関数 fitsemigraph は、当てはめられたラベルとスコアが含まれる Mdl を返します。

メモ

この引数は、Method 値が 'labelpropagation' または 'labelspreading' である場合のみ有効です。

例: 'IterationLimit',2e3

データ型: single | double

Tolerance — 以後の反復におけるスコア差の絶対値に対する許容誤差

1e-3 (既定値) | 非負のスカラー

以後の反復におけるスコア差の絶対値に対する許容誤差。'Tolerance' と非負のスカラーで構成されるコンマ区切りのペアとして指定します。

メモ

この引数は、Method 値が 'labelpropagation' または 'labelspreading' である場合のみ有効です。

例: 'Tolerance',1e-4

データ型: single | double

分類オプション

CategoricalPredictors — カテゴリカル予測子のリスト

正の整数のベクトル | logical ベクトル | 文字行列 | string 配列 | 文字ベクトルの cell 配列 | 'all'

カテゴリカル予測子のリスト。次の表のいずれかの値として指定します。

値	説明
正の整数のベクトル	ベクトルの各エントリは、対応する予測子がカテゴリカルであることを示すインデックス値です。インデックス値の範囲は 1 ～ p です。p はモデルの学習に使用した予測子の数です。 fitsemigraph が入力変数のサブセットを予測子として使用する場合、関数はサブセットのみを使用して予測子にインデックスを作成します。応答変数、観測値の重みの変数、または関数で使用されないその他の変数は、いずれも CategoricalPredictors 値でカウントされません。
logical ベクトル	true というエントリは、対応する予測子がカテゴリカルであることを意味します。ベクトルの長さは p です。
文字行列	行列の各行は予測子変数の名前です。名前は PredictorNames のエントリに一致しなくてはなりません。文字行列の各行が同じ長さになるように、名前を余分な空白で埋めてください。
文字ベクトルの cell 配列または string 配列	配列の各要素は予測子変数の名前です。名前は PredictorNames のエントリに一致しなくてはなりません。
"all"	すべての予測子がカテゴリカルです。

既定では、予測子データがテーブル内にある場合、fitsemigraph は、その変数が logical ベクトル、categorical ベクトル、文字配列、string 配列のいずれか、あるいは文字ベクトルの cell 配列である場合に、変数を categorical であると見なします。順序カテゴリカル変数はサポートされません。予測子データが行列である場合、fitsemigraph はすべての予測子が連続的であると見なします。他の予測子をカテゴリカル予測子として指定するには、名前と値のペアの引数 'CategoricalPredictors' を使用してそれらを指定します。

fitsemigraph は、正の整数値を各カテゴリに割り当てることにより、カテゴリカル変数を数値変数として符号化します。カテゴリカル予測子を使用する場合、必ず適切な距離計量 (Distance) を使用するようにしてください。

例: 'CategoricalPredictors','all'

データ型: single | double | logical | char | string | cell

ClassNames — ラベル付けに使用するクラスの名前

categorical 配列 | 文字配列 | string 配列 | logical ベクトル | 数値ベクトル | 文字ベクトルの cell 配列

ラベル付けに使用するクラスの名前。'ClassNames' と、categorical 配列、文字配列、string 配列、logical ベクトル、数値ベクトルのいずれか、あるいは文字ベクトルの cell 配列で構成されるコンマ区切りのペアとして指定します。ClassNames のデータ型は Y と同じでなければなりません。

ClassNames が文字配列の場合、各要素は配列の 1 つの行に対応しなければなりません。

'ClassNames' の使用目的は次のとおりです。

• クラスの順序を指定する。

• クラスの順序に対応する入力または出力引数の次元の順序を指定する。たとえば、Mdl.LabelScores に含まれる分類スコアの列の順序を指定するために 'ClassNames' を使用します。

• ラベル付けにクラスのサブセットを選択する。たとえば、Y に含まれているすべての異なるクラス名の集合が {'a','b','c'} であるとします。クラス 'a' および 'c' の観測値のみを使用するには、'ClassNames',{'a','c'} と指定します。

ClassNames の既定値は、Y に含まれているすべての異なるクラス名の集合です。

例: 'ClassNames',{'b','g'}

データ型: categorical | char | string | logical | single | double | cell

PredictorNames — 予測子変数名

一意な名前の string 配列 | 一意な文字ベクトルの cell 配列

予測子変数名。'PredictorNames' と一意な名前の string 配列または一意な文字ベクトルの cell 配列から構成されるコンマ区切りのペアとして指定します。'PredictorNames' の機能は、予測子データの提供方法によって決まります。

• X、Y、および UnlabeledX を指定した場合、'PredictorNames' を使用して X および UnlabeledX 内の予測子変数に名前を割り当てることができます。

  • PredictorNames 内の名前の順序は、X の列の順序に一致しなければなりません。つまり、PredictorNames{1} は X(:,1) の名前、PredictorNames{2} は X(:,2) の名前であり、他も同様です。また、size(X,2) と numel(PredictorNames) は等しくなければなりません。

  • 既定では PredictorNames は {'x1','x2',...} です。

• Tbl および UnlabeledTbl を指定する場合、'PredictorNames' を使用して、使用する予測子変数を選択できます。つまり、fitsemigraph は PredictorNames の予測子変数と応答変数のみを使用して、ラベル付けされていないデータにラベルを付けます。

  • PredictorNames は Tbl.Properties.VariableNames のサブセットでなければならず、応答変数の名前を含めることはできません。

  • 既定では、すべての予測子変数の名前が PredictorNames に格納されます。

  • 'PredictorNames' と formula の両方ではなく、いずれか一方を使用して予測子を指定することをお勧めします。

例: 'PredictorNames',{'SepalLength','SepalWidth','PetalLength','PetalWidth'}

データ型: string | cell

ResponseName — 応答変数名

'Y' (既定値) | 文字ベクトル | string スカラー

応答変数名。'ResponseName' と文字ベクトルまたは string スカラーから構成されるコンマ区切りのペアとして指定します。

• Y を指定した場合、'ResponseName' を使用して応答変数の名前を指定できます。

• ResponseVarName または formula を指定した場合、'ResponseName' を使用することはできません。

例: 'ResponseName','response'

データ型: char | string

Standardize — 予測子データを標準化するためのフラグ

false または 0 (既定値) | true または 1

予測子データを標準化するためのフラグ。'Standardize' と数値または logical の 0 (false) または 1 (true) で構成されるコンマ区切りのペアとして指定します。'Standardize',true を設定すると、ソフトウェアは、ラベル付けされた予測子データとラベル付けされていない予測子データを組み合わせて、対応する列の平均値と標準偏差により、各数値予測子変数に対してセンタリングとスケーリングを行います。ソフトウェアは、カテゴリカル予測子を標準化しません。

例: 'Standardize',true

データ型: double | logical

距離計量オプション

Distance — 距離計量

文字ベクトル | string スカラー

距離計量。'Distance' と文字ベクトルまたは string スカラーで構成されるコンマ区切りのペアとして指定します。

• すべての予測子変数が連続 (数値) 変数である場合、次の距離計量のうちの 1 つを指定できます。

  値	説明
  'euclidean'	ユークリッド距離
  'seuclidean'	標準化されたユークリッド距離 — 観測値間の各座標差は、標準偏差 S = std(PD,'omitnan') の対応する要素で除算することによりスケーリングされます。ここで、PD は予測子データ (ラベル付けされたデータとラベル付けされていないデータの両方) です。他のスケール パラメーターを指定するには、名前と値のペアの引数 'Scale' を使用します。
  'mahalanobis'	マハラノビス距離 — 既定の設定では、この距離は C = cov(PD,'omitrows') (PD の共分散) を使用して計算されます。共分散行列の値を変更するには、名前と値のペアの引数 'Cov' を使用します。
  'minkowski'	ミンコフスキー距離 — 既定の指数は 2 です。別の指数を指定するには、'P' 名前と値のペアの引数を使用します。
  'chebychev'	チェビシェフ距離 (最大座標差)
  'cityblock'	市街地距離
  'correlation'	1 から、観測値間の標本相関を減算 (値の系列として処理)
  'cosine'	1 から、ベクトルとして扱われる観測間の夾角の余弦を減算
  'spearman'	1 から観測値間の標本スピアマン順位相関係数を減算 (値の系列として処理)

  メモ

  これらの距離計量のうちの 1 つを指定しており、予測子データにカテゴリカル予測子が含まれる場合、ソフトウェアは、各カテゴリカル予測子を距離計算用の数値変数として扱います。各カテゴリは正の整数で表されます。Distance の値は学習済みモデルの CategoricalPredictors プロパティに影響しません。

• すべての予測子変数がカテゴリカル変数である場合、次の距離計量のうちの 1 つを指定できます。

  値	説明
  'hamming'	ハミング距離 (異なる座標の比率)
  'jaccard'	1 からジャカード係数 (異なる非ゼロ座標の比率) を減算

  メモ

  これらの距離計量のうちの 1 つを指定しており、予測子データに連続 (数値) 予測子が含まれる場合、ソフトウェアは、各連続予測子を距離計算用のカテゴリカル変数として扱います。Distance の値は学習済みモデルの CategoricalPredictors プロパティに影響しません。

• 予測子変数が連続 (数値) 変数とカテゴリカル変数の混合である場合、次の距離計量のうちの 1 つを指定できます。

  値	説明
  'goodall3'	異形グドール距離
  'ofd'	出現頻度距離

すべての予測子変数が連続変数であれば、既定値は 'euclidean' です。予測子変数のいずれかがカテゴリカル変数であれば、既定値は 'goodall3' です。さまざまな距離計量の詳細については、距離計量を参照してください。

例: 'Distance','ofd'

データ型: char | string

Scale — 標準化されたユークリッド距離計量のスケール パラメーター

非負のベクトル

標準化されたユークリッド距離計量のスケール パラメーター。'Scale' と非負のベクトルで構成されるコンマ区切りのペアとして指定します。Scale の長さは予測子の数と同じです。2 つの観測値間の各座標差は、Scale の対応する要素でスケーリングされます。

既定のスケール パラメーターは std(PD,'omitnan') です。ここで、PD は予測子データ (ラベル付けされたデータとラベル付けされていないデータの両方) です。

メモ

この引数は、Distance が 'seuclidean' である場合のみ有効です。

例: 'Scale',iqr(X)

データ型: single | double

Cov — マハラノビス距離計量の共分散行列

正定値行列

マハラノビス距離計量の共分散行列。'Cov' と p 行 p 列の正定値行列で構成されるコンマ区切りのペアとして指定します。p は予測子の数です。

既定の共分散行列は cov(PD,'omitrows') です。ここで、PD は予測子データ (ラベル付けされたデータとラベル付けされていないデータの両方) です。

メモ

この引数は、Distance が 'mahalanobis' である場合のみ有効です。

例: 'Cov',eye(3)

データ型: single | double

P — ミンコフスキー距離計量の指数

2 (既定値) | 正のスカラー

ミンコフスキー距離計量の指数。'P' と正のスカラー値をコンマで区切って指定します。

メモ

この引数は、Distance が 'minkowski' である場合のみ有効です。

例: 'P',3

データ型: single | double

グラフ オプション

SimilarityGraph — 類似度グラフのタイプ

'knn' (既定値) | 'epsilon'

ラベル付けアルゴリズムで使用する類似度グラフのタイプ。'SimilarityGraph' と次のいずれかの値で構成されるコンマ区切りのペアとして指定します。

値	説明	グラフ固有の名前と値のペアの引数
'knn'	最近傍を使用してグラフを作成します。	'NumNeighbors' — 類似度グラフの作成に使用される最近傍の個数 'KNNGraphType' — 最近傍グラフのタイプ
'epsilon'	半径探索を使用してグラフを作成します。このオプションを使用する場合、Radius の値を指定しなければなりません。	'Radius' — 類似度グラフの作成に使用される最近傍の探索半径

詳細は、類似度グラフを参照してください。

例: 'SimilarityGraph','epsilon','Radius',2

データ型: char | string

NumNeighbors — 最近傍の個数

正の整数スカラー

類似度グラフの作成に使用される最近傍の数。'NumNeighbors' と正の整数スカラーで構成されるコンマ区切りのペアとして指定します。

近傍の既定の数は log(n) です。ここで、n は予測子データ (ラベル付けされたデータとラベル付けされていないデータの両方) 内の観測値の数です。

メモ

この引数は、SimilarityGraph が 'knn' である場合のみ有効です。

例: 'NumNeighbors',10

データ型: single | double

KNNGraphType — 最近傍グラフのタイプ

'complete' (既定値) | 'mutual'

最近傍グラフのタイプ。'KNNGraphType' と次のいずれかの値から構成されるコンマ区切りのペアとして指定します。

値	説明
'complete'	i が j の最近傍であるか、j が i の最近傍である場合に、i と j の 2 つの点を接続します。 このオプションでは、類似度行列がより密に表現されます。
'mutual'	i が j の最近傍であり、かつ j が i の最近傍である場合に、i と j の 2 つの点を接続します。 このオプションでは、類似度行列がより希薄に表現されます。

メモ

この引数は、SimilarityGraph が 'knn' である場合のみ有効です。

例: 'KNNGraphType','mutual'

データ型: char | string

Radius — 探索半径

非負のスカラー

類似度グラフの作成に使用される最近傍の探索半径。'Radius' と非負のスカラーで構成されるコンマ区切りのペアとして指定します。

メモ

SimilarityGraph が 'epsilon' の場合、この引数を指定しなければなりません。

例: 'Radius',5

データ型: single | double

KernelScale — スケール係数

1 (既定値) | 'auto' | 正のスカラー

カーネルのスケール係数。'KernelScale' と 'auto' または正のスカラーで構成されるコンマ区切りのペアとして指定します。距離を類似度測定に変換するために、スケール係数が使用されます。

• 'auto' オプションは、'euclidean' および 'seuclidean' の距離計量でのみサポートされます。

• 'auto' を指定した場合、ヒューリスティック手法を使用して適切なスケール係数が選択されます。このヒューリスティック手法では副標本抽出を使用するので、呼び出すたびに推定値が変化する可能性があります。結果を再現するには、fitsemigraph を呼び出す前に rng を使用して乱数シードを設定します。

例: 'KernelScale','auto'

データ型: single | double | char | string

出力引数

Mdl — 半教師ありグラフベース分類器

SemiSupervisedGraphModel オブジェクト

半教師ありグラフベース分類器。SemiSupervisedGraphModel オブジェクトとして返されます。ドット表記を使用してオブジェクト プロパティにアクセスします。たとえば、ラベル付けされていないデータに当てはめられたラベルとそれに対応するスコアを取得するには、Mdl.FittedLabels と Mdl.LabelScores をそれぞれ入力します。

詳細

距離計量

距離計量は、2 つの観測値の間の距離を定義する関数です。fitsemigraph は、連続 (数値) 予測子の多様な距離計量、カテゴリカル予測子、および連続予測子とカテゴリカル予測子の混合をサポートします。

mx 行 n 列のデータ行列 X (mx 個の 1 行 n 列の行ベクトル x₁、x₂、...、x_mx として扱われる) と、my 行 n 列のデータ行列 Y (my 個の 1 行 n 列の行ベクトル y₁、y₂、...、y_my として扱われる) が与えられた場合、ベクトル x_s と y_t の間のさまざまな距離は次のように定義されます。

• 連続 (数値) 変数の距離計量

  • ユークリッド距離

    $$d_{st}^2=(x_s-y_t)(x_s-y_t{)}^{\prime }.$$

    ユークリッド距離はミンコフスキー距離の特殊なケース、p = 2 の場合です。

  • 標準化されたユークリッド距離

    $$d_{st}^2=(x_s-y_t)V^{-1}(x_s-y_t{)}^{\prime },$$

    ここで、V は j 番目の対角要素が (S(j))² である n 行 n 列の対角行列です。S は各次元のスケーリング係数のベクトルです。

  • マハラノビス距離

    $$d_{st}^2=(x_s-y_t)C^{-1}(x_s-y_t{)}^{\prime },$$

    ここで、C は共分散行列です。

  • ミンコフスキー距離

    $$d_{st}=\sqrt[p]{{\displaystyle \sum _{j=1}^n{\left|x_{sj}-y_{tj}\right|}^p}}.$$

    p = 1 という特殊なケースでは、ミンコフスキー距離は市街地距離を与えます。p = 2 という特殊なケースでは、ミンコフスキー距離はユークリッド距離を与えます。p = ∞ という特殊なケースでは、ミンコフスキー距離はチェビシェフ距離を与えます。

  • チェビシェフ距離

    $$d_{st}={\max }_j\left\{\left|x_{sj}-y_{tj}\right|\right\}.$$

    チェビシェフ距離はミンコフスキー距離の特殊なケース、p = ∞ の場合です。

  • 市街地距離

    $$d_{st}={\displaystyle \sum _{j=1}^n\left|x_{sj}-y_{tj}\right|}.$$

    市街地距離はミンコフスキー距離の特殊なケース、p = 1 の場合です。

  • 相関距離

    $$d_{st}=1-\frac{\left(x_s-{\overline{x}}_s\right){\left(y_t-{\overline{y}}_t\right)}^{\prime }}{\sqrt{\left(x_s-{\overline{x}}_s\right){\left(x_s-{\overline{x}}_s\right)}^{\prime }}\sqrt{\left(y_t-{\overline{y}}_t\right){\left(y_t-{\overline{y}}_t\right)}^{\prime }}},$$

    ここで

    $${\overline{x}}_s=\frac{1}{n}{\displaystyle \sum _j{x}_{sj}}$$

    および

    $${\overline{y}}_t=\frac{1}{n}{\displaystyle \sum _j{y}_{tj}}.$$

  • コサイン距離

    $$d_{st}=\left(1-\frac{x_s{y^{\prime }}_t}{\sqrt{\left(x_s{x^{\prime }}_s\right)\left(y_t{y^{\prime }}_t\right)}}\right).$$

  • スピアマン距離は、1 から一連の値として扱われる観測値間の標本スピアマン順位相関係数を引きます。

    $$d_{st}=1-\frac{\left(r_s-{\overline{r}}_s\right){\left(r_t-{\overline{r}}_t\right)}^{\prime }}{\sqrt{\left(r_s-{\overline{r}}_s\right){\left(r_s-{\overline{r}}_s\right)}^{\prime }}\sqrt{\left(r_t-{\overline{r}}_t\right){\left(r_t-{\overline{r}}_t\right)}^{\prime }}},$$

    ここで

    • r_sj は、tiedrank により計算される、x_1j、x_2j、...x_mx,j から取得された x_sj の順位です。

    • r_tj は、tiedrank により計算される、y_1j、y_2j、...y_my,j から取得された y_tj の順位です。

    • r_s および r_t は、x_s および y_t の座標単位の順位ベクトルです。つまり、r_s = (r_s1, r_s2, ... r_sn) および r_t = (r_t1, r_t2, ... r_tn) です。

    • $${\overline{r}}_s=\frac{1}{n}{\displaystyle \sum _j{r}_{sj}}=\frac{\left(n+1\right)}{2}$$.

    • $${\overline{r}}_t=\frac{1}{n}{\displaystyle \sum _j{r}_{tj}}=\frac{\left(n+1\right)}{2}$$.

• カテゴリカル変数の距離計量

  • ハミング距離

    $$d_{st}=(\#(x_{sj}\ne y_{tj})/n).$$

    ハミング距離は、一致しない座標の比率です。

  • Jaccard 距離は、1 からジャカード係数 (異なる非ゼロ座標の比率) を引きます。

    $$d_{st}=\frac{\#\left[\left(x_{sj}\ne y_{tj}\right)\cap \left(\left(x_{sj}\ne 0\right)\cup \left(y_{tj}\ne 0\right)\right)\right]}{\#\left[\left(x_{sj}\ne 0\right)\cup \left(y_{tj}\ne 0\right)\right]}.$$

• 連続 (数値) 変数とカテゴリカル変数の混合の距離計量

  • 異形グドール距離

    この距離は、グドール距離のバリアントであり、他の値の頻度に関係なく、一致する値が互いに離れた場所にある場合に小さな距離を割り当てます。不一致の場合、予測子の距離寄与は 1/(変数の数) です。

  • 出現頻度距離

    一致の場合、出現頻度距離はゼロ距離を割り当てます。不一致の場合、出現頻度距離は、頻度の低い値に高い距離を割り当て、頻度の高い値に低い距離を割り当てます。

類似度グラフ

類似度グラフは、予測子データ (ラベル付けされたデータとラベル付けされていないデータの両方) 内の観測値間のローカルな近傍関係を無向グラフとしてモデル化します。グラフ内のノードは観測値を表し、無向のエッジは観測値間の接続を表します。

任意の 2 つのノード i および j 間のペアワイズ距離 Dist_i,j が正である (またはあるしきい値よりも大きい) 場合、類似度グラフはエッジを使用して 2 つのノードを接続します。2 つのノード間のエッジは、ペアワイズ類似度 S_i,j によって重み付けされます。ここで、指定されたカーネル スケール σ の値に対して $$S_{i,j}=\exp \left(-{\left(\frac{Dis{t}_{i,j}}{\sigma }\right)}^2\right)$$ です。

fitsemigraph は、以下の 2 つの類似度グラフ作成方式をサポートしています。

• "最近傍" 法 (SimilarityGraph が 'knn' の場合 (既定)): fitsemigraph は予測子データ (ラベル付けされたデータとラベル付けされていないデータの両方) 内の最近傍である観測値を接続します。

  • 名前と値のペアの引数 'NumNeighbors' を使用して、最近傍の数を指定します。

  • 名前と値のペアの引数 'KNNGraphType' を使用して、点の接続を 'complete' にするか 'mutual' にするか指定します。

• "半径探索" 法 (SimilarityGraph が 'epsilon' の場合): fitsemigraph はペアワイズ距離が指定した探索半径未満である観測値を接続します。名前と値のペアの引数 'Radius' を使用して、類似度グラフの作成に使用される最近傍の探索半径を指定しなければなりません。

類似度行列

類似度行列は、類似度グラフの行列表現です。n 行 n 列の行列 $$S={(S_{i,j})}_{i,j=1,\dots ,n}$$ には、類似度グラフで接続しているノード間のペアワイズ類似度の値が含まれます。グラフの類似度行列は、隣接行列とも呼ばれます。

類似度グラフのエッジが無向であるため、類似度行列は対称です。Si,j = 0 の値は、類似度グラフのノード i と j が接続していないことを意味します。

アルゴリズム

ソフトウェアは、ラベル付けされた観測値とラベル付けされていない観測値をノードとして使用して類似度グラフ (SimilarityGraph) を作成し、ラベル伝播またはラベル拡散を使用して、ラベル付けされた観測値からラベル付けされていない観測値にラベル情報を分布させます。

ラベル伝播

類似度グラフ内のノードにラベルを伝播するには、次の手順に従って反復ラベル伝播アルゴリズム (Method は 'labelpropagation') を使用します。

1. n 行 K 列の行列 F(0) を開始します。ここで、n はノード (観測値) の数、K はクラスの数です。

   • 最初の l 行は、ラベル付けされた観測値に対応します。各行において、その観測値の真のクラス ラベルに対応する列には 1 が、その他のすべての列には 0 が格納されます。

   • 最後の u 行はラベル付けされていない観測値に対応し、すべての列に 0 が格納されます。

2. 反復 t (t = 1 で開始) において、確率的遷移行列 P を使用して、$$F(t)=PF(t-1)$$ となるように F 行列を更新します。ここで、$$P_{i,j}=\frac{S_{i,j}}{{\displaystyle \sum _{k=1}^n{S}_{i,k}}}$$ となります。

   • P_i,j は、ノード i からノード j にラベル情報が伝達する確率です。

   • S_i,j は、ノード i とノード j の間のエッジの重みです。S_i,j の定義については、類似度グラフを参照してください。

3. 反復 t を完了するには、ラベル付けされた観測値のラベルをクランプします。つまり、F(t) の最初の l 行を F(0) におけるその初期値と等しいまま維持します。

4. F 値が収束するまで、2 番目と 3 番目の手順を繰り返します。IterationLimit 値と Tolerance 値を使用すれば収束を制御できます。

   最後の F 行列は、ラベル付けされたデータおよびラベル付けされていないデータのスコア (LabelScores) に対応します。各観測値 (F 内の行) について、最大のスコアをもつ列は、当てはめられたクラス ラベル (FittedLabels) に対応します。

詳細は、[2]を参照してください。

反復ラベル伝播アルゴリズムを使用する代わりに、厳密法を使用してラベル伝播を行うこともできます (ここで、Method は 'labelpropagationexact' です)。この場合、ラベル付けされていないデータのラベル情報で構成される u 行 K 列の行列は F_U = (I – P_UU)^-1P_ULF_L です。ここで、次のようになります。

• I は単位行列です。

• P_UU および P_UL は、$$P=\left[\begin{array}{cc}{P}_{LL}& P_{LU}\\ P_{UL}& P_{UU}\end{array}\right]$$ となるような P のラベル付けされた部分行列 (L) およびラベル付けされていない部分行列 (U) です。

• F_L は、ラベル付けされたデータのラベル情報で構成される l 行 K 列の行列です。各行において、その観測値の真のクラス ラベルに対応する列には 1 が、その他のすべての列には 0 が格納されます。

F_U 行列は、ラベル付けされていないデータのスコア (LabelScores) に対応します。各観測値 (F_U 内の行) について、最大のスコアをもつ列は、当てはめられたクラス ラベル (FittedLabels) に対応します。詳細は、[3]を参照してください。

ラベル拡散

類似度グラフ内のノードにラベルを拡散するには、次の手順に従って反復拡散伝播アルゴリズム (Method は 'labelspreading') を使用します。

1. n 行 K 列の行列 Y を作成します。ここで、n はノード (または観測値) の数、K はクラスの数です。

   • 最初の l 行は、ラベル付けされた観測値に対応します。各行において、その観測値の真のクラス ラベルに対応する列には 1 が、その他のすべての列には 0 が格納されます。

   • 最後の u 行はラベル付けされていない観測値に対応し、すべての列に 0 が格納されます。

2. n 行 n 列の類似度行列 S を正規化したものとなる行列 A を作成します。ペアワイズ類似度の値 S_i,j は類似度グラフで定義されたものにします。A = D^-1/2SD^-1/2 とします。ここで、D は n 行 n 列の対角行列 $$D=\left[\begin{array}{ccc}{\displaystyle \sum _{j=1}^n{S}_{1,n}}& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \dots & {\displaystyle \sum _{j=1}^n{S}_{n,n}}\end{array}\right]$$ です。

3. 反復 t (t = 1 で開始) において、行列 A および隣接ラベルの重みパラメーター α (Alpha) を使用して、F(t) = αAF(t – 1) + (1 – α)Y となるように F 行列を更新します。F(0) を Y と等しくします。

4. F 値が収束するまで、3 番目の手順を繰り返します。IterationLimit 値と Tolerance 値を使用すれば収束を制御できます。

5. 数列 $${\{F(t)\}}_{t=1,\mathrm{..},T}$$ の上限を取得します。この最後の行列は、ラベル付けされたデータおよびラベル付けされていないデータのスコア (LabelScores) に対応します。各観測値 (行列内の行) について、最大のスコアをもつ列は、当てはめられたクラス ラベル (FittedLabels) に対応します。

反復ラベル拡散アルゴリズムを使用する代わりに、厳密法を使用してラベル拡散を行うこともできます (ここで、Method は 'labelspreadingexact' です)。この場合、ラベル付けされたデータとラベル付けされていないデータのラベル情報で構成される n 行 K 列の行列は F = (I – αA)^-1Y です。ここで、I は単位行列です。F 行列は、ラベル付けされたデータおよびラベル付けされていないデータのスコア (LabelScores) に対応します。各観測値 (F 内の行) について、最大のスコアをもつ列は、当てはめられたクラス ラベル (FittedLabels) に対応します。

詳細は、[1]を参照してください。

参照

[1] Zhou, Dengyong, Olivier Bousquet, Thomas Navin Lal, Jason Weston, and Bernhard Schölkopf. “Learning with Local and Global Consistency.” Advances in Neural Information Processing Systems 16 (NIPS). 2003.

[2] Zhu, Xiaojin, and Zoubin Ghahramani. “Learning from Labeled and Unlabeled Data with Label Propagation.” CMU CALD tech report CMU-CALD-02-107. 2002.

[3] Zhu, Xiaojin, Zoubin Ghahramani, and John Lafferty. “Semi-Supervised Learning Using Gaussian Fields and Harmonic Functions.” The Twentieth International Conference on Machine Learning (ICML). 2003.

バージョン履歴

R2020b で導入

参考

SemiSupervisedGraphModel | predict | fitsemiself

トピック

• 半教師あり学習手法を使用したデータのラベル付け