このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

detectdrift

並べ替え検定を使用してベースライン データとターゲット データの間のドリフトを検出

R2022a 以降

構文

DDiagnostics = detectdrift(Baseline,Target)

DDiagnostics = detectdrift(Baseline,Target,Name=Value)

説明

DDiagnostics = detectdrift(Baseline,Target) は、並べ替え検定を実行して Baseline と Target のデータ セット間の各変数のドリフトを検出し、その結果を DDiagnostics で返します。

DDiagnostics は、DriftDiagnostics オブジェクトです。

DDiagnostics = detectdrift(Baseline,Target,Name=Value) では、1 つ以上の名前と値の引数を使用して追加オプションを指定します。たとえば、変数に使用するメトリクスや順列の最大数を指定できます。

例

潜在的なドリフトについてのベースライン データとターゲット データの比較

2 つの変数をもつベースライン データとターゲット データを生成します。ターゲット データで 2 つ目の変数の分布パラメーターを変化させます。

rng('default') % For reproducibility
baseline = [normrnd(0,1,100,1),wblrnd(1.1,1,100,1)];
target = [normrnd(0,1,100,1),wblrnd(1.2,2,100,1)];

2 つのデータ セットを比較してドリフトを調べます。

DDiagnostics = detectdrift(baseline,target)

DDiagnostics = 
  DriftDiagnostics

              VariableNames: ["x1"    "x2"]
       CategoricalVariables: []
                DriftStatus: ["Stable"    "Drift"]
                    PValues: [0.2850 0.0030]
        ConfidenceIntervals: [2×2 double]
    MultipleTestDriftStatus: "Drift"
             DriftThreshold: 0.0500
           WarningThreshold: 0.1000


  Properties, Methods

DDiagnostics は DriftDiagnostics オブジェクトです。detectdrift により、いくつかのオブジェクト プロパティが表示されます。

推定 "p" 値の信頼区間を表示します。

DDiagnostics.ConfidenceIntervals

ans = 2×2

    0.2572    0.0006
    0.3141    0.0087

1 つ目の変数について、推定 "p" 値の信頼区間の下限が警告しきい値の 0.1 より大きくなっています。そのため、1 つ目の変数のターゲット データはベースライン データと比較して安定していると detectdrift で判定されています。2 つ目の変数については、推定 "p" 値の信頼区間の上限がドリフトしきい値の 0.05 より小さくなっています。そのため、この変数のドリフト ステータスは Drift になります。これは、分布パラメーターにおけるシフトが detectdrift で検出されたことを示します。

detectdrift は、既定では多重仮説検定にボンフェローニの方法を使用します。関数は最初に警告しきい値とドリフトしきい値を "p" 値の数 (この例では 2) で除算します。その後、そのいずれかのしきい値よりも低い "p" 値があるかどうかを調べます。ここでは、2 つ目の "p" 値が修正後のドリフトしきい値よりも低いため、関数はデータ全体の MultipleTestDriftStatus を Drift に設定しています。

両方の変数について、順列の結果を可視化します。

tiledlayout(2,1);
ax1 = nexttile;
plotPermutationResults(DDiagnostics,ax1,Variable="x1")
ax2 = nexttile;
plotPermutationResults(DDiagnostics,ax2,Variable="x2")

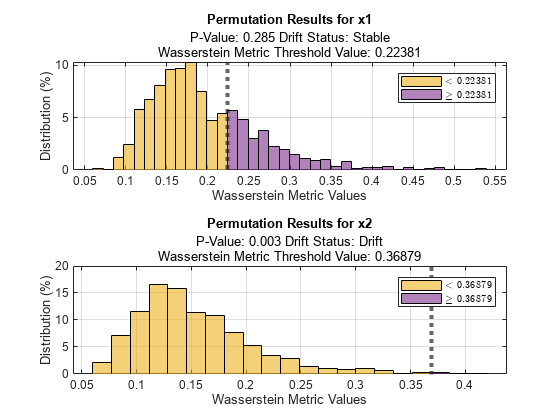
破線より右にあるバーは、しきい値を超えているメトリクス値を示しています。このしきい値は、ベースライン データとターゲット データを使用して detectdrift で計算される各変数の初期メトリクス値です。変数 x1 ではしきい値を超えているバーの数がはるかに多く、この変数についてはベースライン データとターゲット データの間に大きなドリフトがないことを示しています。

データ ドリフト検出のオプションの指定

標本データを読み込みます。

load humanactivity

データ セットの詳細については、コマンド ラインで Description を入力してください。

最初の 250 個の観測値をベースライン データとして割り当て、次の 250 個をターゲット データとして割り当てます。

baseline = feat(1:250,:);
target = feat(251:500,:);

警告しきい値 0.05 とドリフトしきい値 0.01 を使用して、5 番目から 10 番目までの変数についてドリフトを検定します。いずれも連続変数であるため、すべての変数にコルモゴロフ・スミルノフ メトリクスを使用します。多重検定補正として偽発見率法を指定します。

DDiagnostics = detectdrift(baseline(:,5:10),target(:,5:10),WarningThreshold=0.05, ...
        DriftThreshold=0.01,ContinuousMetric="ks",MultipleTestCorrection="fdr")

DDiagnostics = 
  DriftDiagnostics

              VariableNames: ["x1"    "x2"    "x3"    "x4"    "x5"    "x6"]
       CategoricalVariables: []
                DriftStatus: ["Drift"    "Drift"    "Drift"    "Stable"    "Warning"    "Drift"]
                    PValues: [1.0000e-03 1.0000e-03 1.0000e-03 0.8810 0.0110 1.0000e-03]
        ConfidenceIntervals: [2×6 double]
    MultipleTestDriftStatus: "Drift"
             DriftThreshold: 0.0100
           WarningThreshold: 0.0500


  Properties, Methods

推定 "p" 値の信頼区間を表示します。

DDiagnostics.ConfidenceIntervals

ans = 2×6

    0.0000    0.0000    0.0000    0.8593    0.0055    0.0000
    0.0056    0.0056    0.0056    0.9004    0.0196    0.0056

8 番目の変数 (変数名 x4) について、"p" 値の信頼限界の下限が警告しきい値より大きくなっています。そのため、detectdrift はこの変数のドリフト ステータスを "Stable" と判定しています。9 番目の変数 (変数名 x5) については、"p" 値の信頼限界の上限がドリフトしきい値より大きくなっていますが、警告しきい値よりは低くなっています。そのため、detectdrift はこの変数のドリフト ステータスを "Warning" と判定しています。他のすべての変数については、信頼区間がドリフトしきい値より小さいため、ドリフト ステータスは "Drift" です。多重検定補正の偽発見率法に基づいて、関数はデータ全体についてのドリフト ステータスを "Drift" と判定しています。

"p" 値と信頼区間を対応するドリフト ステータスと共に可視化します。

plotDriftStatus(DDiagnostics)

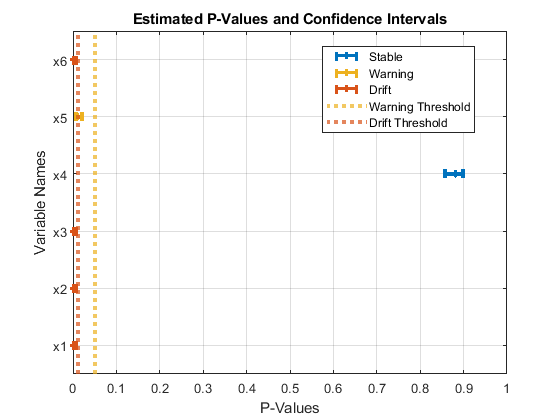
警告しきい値とドリフトしきい値に対する推定 "p" 値と信頼区間のプロットが表示されます。変数 x4 の推定 "p" 値とその信頼区間は警告しきい値より高くなっています。そのため、この変数のドリフト ステータスは "Stable" になります。x5 については、"p" 値の信頼限界の上限がドリフトしきい値より大きくなっていますが、警告しきい値よりは低くなっています。そのため、この変数のドリフト ステータスは "Warning" になります。他のすべての変数については、信頼区間がドリフトしきい値より小さいため、ドリフト ステータスは "Drift" です。

データ ドリフト検出で使用する変数とメトリクスの指定

データ セット NYCHousing2015 を読み込みます。

load NYCHousing2015

データ セットには、2015 年のニューヨーク市における不動産の売上に関する情報を持つ 10 の変数が含まれます。

外れ値を削除し、datetime 配列 (SALEDATE) を月番号に変換します。

idx = isoutlier(NYCHousing2015.SALEPRICE);
NYCHousing2015(idx,:) = [];
NYCHousing2015.SALEDATE = month(NYCHousing2015.SALEDATE);

1 月と 7 月の売上に関する情報としてベースライン データとターゲット データをそれぞれ定義します。

tbl = NYCHousing2015;
baseline = tbl(tbl.SALEDATE==1,:);
target = tbl(tbl.SALEDATE==7,:);

データをシャッフルします。

n = numel(baseline(:,1));
rng(1); % For reproducibility
idx = randsample(n,n);
baseline = baseline(idx,:);
n = numel(target(:,1));
idx = randsample(n,n);
target = target(idx,:);

ベースライン データとターゲット データの間の潜在的なドリフトを検定します。カテゴリカル変数と各変数で使用するメトリクスを指定します。

DDiagnostics = detectdrift(baseline(1:1500,:),target(1:1500,:), ...
    VariableNames=["BOROUGH","BUILDINGCLASSCATEGORY","LANDSQUAREFEET","GROSSSQUAREFEET","SALEPRICE"], ...
    CategoricalVariables=["BOROUGH","BUILDINGCLASSCATEGORY"], ...
    Metrics=["Hellinger","Hellinger","ad","ks","energy"])

DDiagnostics = 
  DriftDiagnostics

              VariableNames: ["BOROUGH"    "BUILDINGCLASSCATEGORY"    "LANDSQUAREFEET"    "GROSSSQUAREFEET"    "SALEPRICE"]
       CategoricalVariables: [1 2]
                DriftStatus: ["Drift"    "Stable"    "Drift"    "Drift"    "Drift"]
                    PValues: [0.0260 0.1440 0.0070 0.0230 0.0110]
        ConfidenceIntervals: [2×5 double]
    MultipleTestDriftStatus: "Drift"
             DriftThreshold: 0.0500
           WarningThreshold: 0.1000


  Properties, Methods

detectdrift により、BUILDINGCLASSCATEGORY を除くすべての変数について、ベースライン データとターゲット データの間でドリフトが識別されています。

推定 "p" 値の信頼区間を表示します。

DDiagnostics.ConfidenceIntervals

ans = 2×5

    0.0171    0.1228    0.0028    0.0146    0.0055
    0.0379    0.1673    0.0144    0.0343    0.0196

SALEPRICE のヒストグラムをプロットします。

plotHistogram(DDiagnostics,Variable="SALEPRICE")

1 月と比較した 7 月の売価のシフトがヒストグラムに表示されます。

SALEPRICE のベースライン データとターゲット データについての経験的累積分布関数をプロットします。

plotEmpiricalCDF(DDiagnostics,Variable="SALEPRICE")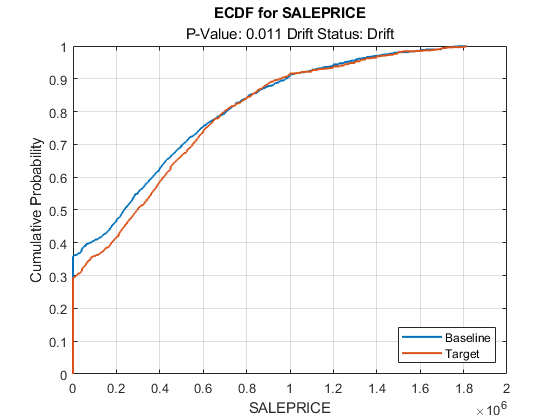

SALEPRICE の順列の結果をプロットします。

plotPermutationResults(DDiagnostics,Variable="SALEPRICE")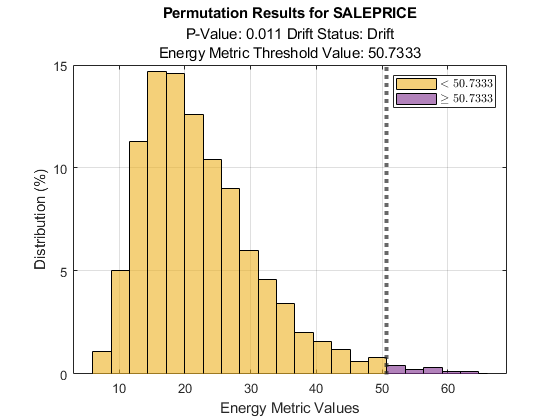

"p" 値の推定なしのメトリクスの計算

3 つの変数をもつベースライン データとターゲット データを生成します。ターゲット データで 2 つ目と 3 つ目の変数の分布パラメーターを変化させます。

rng('default') % For reproducibility
baseline = [normrnd(0,1,100,1),wblrnd(1.1,1,100,1),betarnd(1,2,100,1)];
target = [normrnd(0,1,100,1),wblrnd(1.2,2,100,1),betarnd(1.7,2.8,100,1)];

"p" 値を推定せずに、ベースライン データとターゲット データの間ですべての変数の初期メトリクスを計算します。

DDiagnostics = detectdrift(baseline,target,EstimatePValues=false)

DDiagnostics = 
  DriftDiagnostics

           VariableNames: ["x1"    "x2"    "x3"]
    CategoricalVariables: []
                 Metrics: ["Wasserstein"    "Wasserstein"    "Wasserstein"]
            MetricValues: [0.2022 0.3468 0.0559]


  Properties, Methods

detectdrift により、ベースライン データとターゲット データを使用して各変数の初期メトリクス値のみが計算されます。並べ替え検定および "p" 値の推定に関連付けられたプロパティについては、空になるか NaN が格納されます。

summary(DDiagnostics)

          MetricValue       Metric    
          ___________    _____________

    x1      0.20215      "Wasserstein"
    x2      0.34676      "Wasserstein"
    x3     0.055922      "Wasserstein"

関数 summary により、初期メトリクス値と指定した各変数に使用されるメトリクスのみが表示されます。

plotDriftStatus と plotPermutationResults では、"p" 値を推定せずにメトリクスを計算すると、プロットが生成されずに警告メッセージが返されます。plotEmpiricalCDF と plotHistogram では、既定では 1 つ目の変数についての ecdf とヒストグラムがそれぞれプロットされます。どちらの場合も、"p" 値および変数に関連付けられているドリフト ステータスについては NaN が返されます。

plotEmpiricalCDF(DDiagnostics)

plotHistogram(DDiagnostics)

入力引数

Baseline — ベースライン データ

数値配列 | categorical 配列 | table

ベースライン データ。数値配列、categorical 配列、または table として指定します。Baseline と Target のデータは同じデータ型でなければなりません。入力データが categorical 配列である場合、detectdrift は各列を独立したカテゴリカル変数として扱います。

データ型: single | double | categorical | table

Target — ターゲット データ

数値配列 | categorical 配列 | table

ターゲット データ。数値配列、categorical 配列、または table として指定します。Baseline と Target のデータは同じデータ型でなければなりません。入力データが categorical 配列である場合、detectdrift は各列を独立したカテゴリカル変数として扱います。

データ型: single | double | categorical | table

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで Name は引数名、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

例: detectdrift(Baseline,Target,WarningThreshold=0.05,DriftThreshold=0.01,VariableNames=["Weight","MPG"],ContinuousMetrics="ad") は、警告しきい値を 0.05、ドリフトしきい値を 0.01 に設定し、ドリフト検出用に検定する変数として Weight と MPG を指定し、すべての連続変数の検定に使用するメトリクスとしてアンダーソン・ダーリングを指定します。

VariableNames — ドリフトを解析する変数

string | 一意の string の配列 | 文字ベクトル | 文字ベクトルの cell 配列

ドリフトを解析する変数。string、一意の string の配列、文字ベクトル、または文字ベクトルの cell 配列として指定します。

例: VariableNames=["x1","x3"]

データ型: string | char | cell

CategoricalVariables — カテゴリカル変数のリスト

"all" | string | 一意の string の配列 | 文字ベクトル | 一意な文字ベクトルの cell 配列 | 整数インデックスのベクトル | logical インデックスのベクトル

カテゴリカル変数のリスト。"all"、string、一意の string の配列、文字ベクトル、一意の文字ベクトルの cell 配列、整数インデックスのベクトル、または logical インデックスのベクトルとして指定します。

detectdrift は、ordinal データ型、nominal データ型、または順序インジケーターが true に設定された categorical データ型をカテゴリカル変数として扱います。

例: CategoricalVariables="Zone"

データ型: single | double | logical | string | cell

DriftThreshold — ドリフト検出のしきい値

0.05 (既定値) | 0 から 1 までのスカラー値

ドリフト検出のしきい値。0 から 1 までのスカラー値として指定します。

detectdrift は、ドリフトしきい値を警告しきい値と共に使用してドリフト ステータスを判定します。DriftThreshold の値は WarningThreshold の値より厳密に低くなければなりません。

推定 p 値の信頼区間が (Lower,Upper) の場合、detectdrift はドリフト ステータスを次のように判定します。

ドリフト ステータス	条件
Drift	Upper < DriftThreshold
Warning	DriftThreshold < Lower < WarningThreshold または DriftThreshold < Upper < WarningThreshold
Stable	Lower > WarningThreshold

例: DriftThreshold=0.01

データ型: single | double

WarningThreshold — 潜在的なドリフトの警告のしきい値

0.1 (既定値) | 0 から 1 までのスカラー値

潜在的なドリフトの警告のしきい値。0 から 1 までのスカラー値として指定します。

detectdrift は、警告しきい値をドリフトしきい値と共に使用してドリフト ステータスを判定します。WarningThreshold の値は DriftThreshold の値より厳密に大きくなければなりません。

推定 p 値の信頼区間が (Lower,Upper) の場合、detectdrift はドリフト ステータスを次のように判定します。

ドリフト ステータス	条件
Drift	Upper < DriftThreshold
Warning	DriftThreshold < Lower < WarningThreshold または DriftThreshold < Upper < WarningThreshold
Stable	Lower > WarningThreshold

例: WarningThreshold=0.05

データ型: single | double

MaxNumPermutations — 順列の最大数

1000 (既定値) | 正の整数値

順列の最大数。正の整数値として指定します。detectdrift は、ドリフト ステータスを判定するか MaxNumPermutations に達するまで、ヒューリスティックなアルゴリズムに従って順列の試行回数を対数的に増やしていきます。順列の最大数に達してもドリフト ステータスを判定できない場合、detectdrift はドリフト ステータスを "Warning" に設定します。

例: MaxNumPermutations=1500

データ型: single | double

Metrics — 各変数のドリフト検出に使用するメトリクス

string | string ベクトル | 文字ベクトル | 文字ベクトルの cell 配列 | 関数ハンドル | 関数ハンドルの cell 配列 | 構造体

各変数のドリフト検出に使用するメトリクス。次のいずれかとして指定します。

• 1 つ以上の組み込みメトリクスを表す string、string ベクトル、文字ベクトル、または文字ベクトルの cell 配列。

  連続変数の組み込みメトリクス

  値	定義
  "wasserstein"	ワッサースタイン
  "energy"	エネルギー
  "ks"	コルモゴロフ・スミルノフ
  "ad"	アンダーソン・ダーリング

  カテゴリカル変数の組み込みメトリクス

  値	定義
  "tv"	全変動
  "psi"	母集団安定性指標
  "hellinger"	ヘリンジャー
  "chi2"	カイ二乗
  "bhattacharyya"	バタチャリア

• 関数ハンドルまたは関数ハンドルの cell 配列。関数ハンドル FUN をメトリクスとして指定する場合、detectdrift で次のように呼び出します。

  FUN(BaselineVariable,TargetVariable),

  ここで、BaselineVariable は Baseline の変数、TargetVariable は Target の変数です。FUN の出力はメトリクス値を表すスカラーでなければなりません。

• 構造体または構造体の cell 配列。各構造体に関数ハンドルを値とする単一のフィールドを含めます。構造体を渡す場合、detectdrift はフィールド名をメトリクス名として使用します。関数ハンドルが無名の場合、その名前が detectdrift で 'CustomMetric_i' と指定されます。ここで、i は Metrics における変数の位置です。

Metrics には VariableNames の変数ごとに 1 つの値を格納する必要があり、サイズは VariableNames のサイズと等しくなければなりません。

Metrics を使用してメトリクスを指定する場合、ContinuousMetric または CategoricalMetric を使用して指定することはできません。

例: Metrics=["wasserstein","psi","hellinger"]

データ型: string | cell | function_handle | struct

ContinuousMetric — 連続変数のドリフト検出のメトリクス

"wasserstein" (既定値) | string | 文字ベクトル | 関数ハンドル | 構造体

連続変数のドリフト検出のメトリクス。次のいずれかとして指定します。

• 1 つ以上の組み込みメトリクスを表す string または文字ベクトル。

  連続変数の組み込みメトリクス

  値	定義
  "wasserstein"	ワッサースタイン
  "energy"	エネルギー
  "ks"	コルモゴロフ・スミルノフ
  "ad"	アンダーソン・ダーリング

• 関数ハンドル。次のように呼び出します。

  FUN(BaselineVariable,TargetVariable),

  ここで、BaselineVariable は Baseline の変数、TargetVariable は Target の変数です。FUN の出力はメトリクス値を表すスカラーでなければなりません。

  関数ハンドルが無名でない場合、detectdrift は指定された関数ハンドルからメトリクス名を抽出します。関数ハンドルが無名である場合は、メトリクスの名前が 'CustomContinuousMetric' と指定されます。

• 関数ハンドルを値とする単一のフィールドをもつ構造体。この場合、detectdrift はフィールド名をメトリクス名として使用します。

ContinuousMetric を指定する場合、Metrics を使用して他のメトリクスを指定することはできません。

例: ContinuousMetric="ks"

データ型: string | char | function_handle | struct

CategoricalMetric — カテゴリカル変数のドリフト検出のメトリクス

"hellinger" (既定値) | string | 文字ベクトル | 関数ハンドル | 構造体

カテゴリカル変数のドリフト検出のメトリクス。次のいずれかとして指定します。

• 1 つ以上の組み込みメトリクスを表す string または文字ベクトル。

  カテゴリカル変数の組み込みメトリクス

  値	定義
  "tv"	全変動
  "psi"	母集団安定性指標
  "hellinger"	ヘリンジャー
  "chi2"	カイ二乗
  "bhattacharyya"	バタチャリア

• 関数ハンドル。次のように呼び出します。

  FUN(BaselineVariable,TargetVariable),

  ここで、BaselineVariable は Baseline の変数、TargetVariable は Target の変数です。FUN の出力はメトリクス値を表すスカラーでなければなりません。

  関数ハンドルが無名でない場合、detectdrift は指定された関数ハンドルからメトリクス名を抽出します。関数ハンドルが無名である場合は、メトリクスの名前が 'CustomCategoricalMetric' と指定されます。

• 関数ハンドルを値とする単一のフィールドをもつ構造体。この場合、detectdrift はフィールド名をメトリクス名として使用します。

CategoricalMetric を指定する場合、Metrics を使用して他のメトリクスを指定することはできません。

例: CategoricalMetric="chi2"

データ型: string | char | function_handle | struct

MultipleTestCorrection — 多重仮説検定の補正方法

"bonferroni" (既定値) | "fdr"

多重仮説検定の補正方法。次のいずれかとして指定します。

• "bonferroni" – ボンフェローニ補正。ドリフト検出用に k 個の変数が指定された場合、detectdrift は警告しきい値とドリフトしきい値のそれぞれを k で除算して修正します。その後、関数は修正後のしきい値よりも小さい p 値があるかどうかをチェックしてドリフト ステータスを判定します。

• "fdr" – 偽発見率 (FDR) 法。detectdrift で Benjamini-Hochberg の手法を使用して偽発見率を計算します。ドリフト検出用に k 個の変数が指定された場合、FDR 法では次の手順で処理されます。

  1. 指定された変数に対応する p 値をランク付けします。

  2. ランク 1 から k までを変数の数 k で除算して Q = [1/k, 2/k, 3/k ,…, k/k] を取得します。

  3. 並べ替えられたそれぞれの p 値の警告しきい値とドリフトしきい値について、対応する q の値を警告しきい値とドリフトしきい値の初期値に乗算してそれぞれ修正します。たとえば、ランク 3 の修正後の警告しきい値は (WarningThreshold)*3/k です。

  4. 並べ替えられた p 値について、対応する修正後の警告しきい値またはドリフトしきい値よりも小さいものがあるかどうかをチェックしてドリフト ステータスを判定します。

多重検定の補正方法は、多変数のドリフトの保守的な推定を提供します。

例: MultipleTestCorrection="fdr"

Options — 並列計算と乱数ストリーム設定のオプション

構造体

並列計算と乱数ストリーム設定のオプション。構造体として指定します。statset を使用して Options 構造体を作成します。次の表は、オプションのフィールドとその値の一覧です。

フィールド名	値	既定の設定
UseParallel	並列計算を行う場合は、この値を true に設定します。	false
UseSubstreams	再現可能な方法で計算する場合は、この値を true に設定します。 再現性のある計算を行うには、Streams をサブストリームを許可する型 ("mlfg6331_64" または "mrg32k3a") に設定します。	false
Streams	RandStream オブジェクトまたはそのようなオブジェクトの cell 配列としてこの値を指定します。UseParallel の値が true でなく、UseSubstreams の値も false でない場合、単一オブジェクトを使用します。この場合は、並列プールと同じサイズの cell 配列を使用します。	Streams を指定しなかった場合、detectdrift は既定のストリームを使用します。

メモ

並列計算を行うには、Parallel Computing Toolbox™ が必要です。

例: Options=statset(UseParallel=true,UseSubstreams=true,Streams=RandStream("mlfg6331_64"))

データ型: struct

EstimatePValues — p 値の推定のインジケーター

true (既定値) | false

並べ替え検定における p 値の推定のインジケーター。true または false として指定します。EstimatePValues=false を指定すると、detectdrift はメトリクスのみを計算します。

例: EstimatePValues=false

出力引数

DDiagnostics — ドリフト検出用の並べ替え検定の結果

DriftDiagnostics オブジェクト

ドリフト検出用の並べ替え検定の結果。DriftDiagnostics オブジェクトとして返されます。detectdrift で表示されるプロパティは次のとおりです。

プロパティ名	説明
VariableNames	ドリフト検出用に解析された変数
CategoricalVariables	データ内のカテゴリカル変数のインデックス
DriftStatus	各変数のドリフト ステータス
PValues	各変数の推定 p 値
ConfidenceIntervals	推定 p 値の 95% 信頼区間の範囲
MultipleTestDriftStatus	データ全体のドリフト ステータス
DriftThreshold	ドリフト ステータスを判定するしきい値
WarningThreshold	警告ステータスを判定するしきい値

プロパティとその説明の完全な一覧については、DriftDiagnostics のリファレンス ページを参照してください。

アルゴリズム

並べ替え検定

detectdrift では、Baseline データの各変数と Target データの対応する変数のドリフト ステータスを並べ替え検定[1]を使用して判定します。並べ替え検定は、帰無仮説のもとでメトリクス (検定統計量) の分布を取得するノンパラメトリックな統計的有意性検定です。そのメトリクスの値を Baseline と Target におけるすべての可能な変数の並べ替えのもとで計算します。変数や観測値の数によっては、すべての可能な順列の試行が実行不可能な場合があります。そのため、detectdrift では、変数のメトリクスを適切に推定できる十分な数の順列を実行します。

帰無仮説 (ドリフトなし) において、並べ替え検定で記録されるメトリクスの多くの値が初期検定統計量と同様に極端になることがあります。これは、ベースライン データとターゲット データで、指定した変数の観測値が同じ分布から派生する信頼度が十分に高いことを示しています。そのため、ドリフトの証拠は見つからず、detectdrift は帰無仮説を棄却できません。

初期検定統計量が外れ値として識別されると、detectdrift は帰無仮説を棄却します。これは、ベースライン データとターゲット データで、指定した変数の観測値が異なる分布から派生する信頼度が十分に高いことを示しています。そのため、ドリフトが検出されます。

detectdrift では、次の手順で並べ替え検定を実行します。

• ベースライン データの観測値が m 個でターゲット データの観測値が n 個の指定された変数について、detectdrift は元のデータからメトリクスの初期値を計算します。

• 次に、関数はベースライン データとターゲット データで変数の観測値を並べ替え、それらをサイズが m と n の 2 つのベクトルにそれぞれ分割します。その後、関数は同じメトリクス値を計算します。detectdrift は、この手順を MaxNumPermutations の回数だけ繰り返し、指定されたメトリクスの分布を取得します。

• p 値の推定は p = x/perm です。ここで、x は順列から取得されたメトリクス値が初期メトリクス値の値よりも大きくなる回数、perm は順列の数です。x の二項分布の仮定により、detectdrift は p 値の 95% 信頼区間を [~,CI] = binofit(x,perm,0.05) を使用して推定します。

p 値の信頼区間を (Lower, Upper) とすると、detectdrift は次の条件に基づいてドリフト ステータスを判定します。

ドリフト ステータス	条件
Drift	Upper < DriftThreshold
Warning	DriftThreshold < Lower < WarningThreshold または DriftThreshold < Upper < WarningThreshold
Stable	Lower > WarningThreshold

メトリクス

detectdrift では、ベースライン データとターゲット データの間のドリフトを検出するための並べ替え検定において、次のメトリクスを検定統計量として使用します。

連続変数のメトリクス

関数 detectdrift は、最初に以下を定義します。

• 共通領域におけるベースライン データの経験累積分布関数 (ecdf) を表す $$E_b\left(x\right)$$

• 共通領域におけるターゲット データの ecdf を表す $$E_t\left(x\right)$$

• すべてのデータの結合した ecdf を表す $$D\left(x\right)$$ とビンのエッジ間の差異を表す w

次に、detectdrift は連続変数のメトリクスを次のように計算します。

• ワッサースタイン

  $$W={\displaystyle \sum _{x}w*\left|E_b\left(x\right)-E_t\left(x\right)\right|}$$

• エネルギー

  $$En=\sqrt{2*{\displaystyle \sum _{x}w*{\left|E_b\left(x\right)-E_t\left(x\right)\right|}^2}}$$

• コルモゴロフ・スミルノフ

  $$KS=\max \left|E_b\left(x\right)-E_t\left(x\right)\right|$$

• アンダーソン・ダーリング

  $$AD={{\displaystyle \sum _x\left(\frac{\left|E_b\left(x\right)-E_t\left(x\right)\right|}{\sqrt{\left(m+n\right)D\left(x\right)*\left(1-D\left(x\right)\right)}}\right)}}^2$$

  m と n は、それぞれベースライン データとターゲット データの観測値の数です。

カテゴリカル変数のメトリクス

関数 detectdrift は、以下を定義します。

• ベースライン データとターゲット データを結合 (それらが同じ領域にあると見なして結合) することで判定されるビン内のベースライン データの割合を表す $$H_b\left(x\right)$$

• ベースライン データとターゲット データを結合することで判定されるビン内のターゲット データの割合を表す $$H_t\left(x\right)$$

次に、detectdrift はカテゴリカル変数のメトリクスを次のように計算します。

• 全変動

  $$TV=0.5*{\displaystyle \sum _x\left|H_b\left(x\right)-H_t\left(x\right)\right|}$$

• 母集団安定性指標

  $$PSI=\max \left(0,{\displaystyle \sum _x\log \left(\frac{H_t\left(x\right)}{H_b\left(x\right)}\right)\left(H_t\left(x\right)-H_b\left(x\right)\right)}\right)$$

• カイ二乗

  $${\chi }^2={\displaystyle \sum _x\frac{{\left(H_t\left(x\right)-H_b\left(x\right)\right)}^2}{H_b\left(x\right)}}$$

• バタチャリア

  $$B=\max \left(0,-\log \left(\min \left(1,{\displaystyle \sum _x\sqrt{H_b\left(x\right)*H_t\left(x\right)}}\right)\right)\right)$$

• ヘリンジャー

  $$H=\max \left(0,\sqrt{1-\left(\min \left(1,{\displaystyle \sum _x\sqrt{H_b\left(x\right)*H_t\left(x\right)}}\right)\right)}\right)$$

detectdrift は、空のビン (カテゴリ) を処理するために各ビンのヒストグラムのビンのカウント数に 0.5 の補正係数を追加します。これは、パラメーター p (変数の値がそのカテゴリに含まれる確率) が事前分布 Beta(0.5,0.5) をもつという仮定 (分布パラメーターに関するジェフリーズ事前分布の仮定) と同等です。

参照

[1] Hesterbeg,Tim, David S. Moore, Shaun Monaghan, Ashley Clipson, and Rachel Epstein. "Bootstrap Methods and Permutation Tests" in Introduction to the Practice of Statistics. 7th ed, W.H. Freeman, pp. 1–57, 2010.

[2] Benjamini, Yoav, and Yosef Hochberg. "Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing." Journal of the Royal Statistical Society, Series B (Methodological). Vol. 57, No. 1, pp. 289-300, 1995.

[3] Villani, Cédric. Topics in Optimal Transportation. Graduate Studies in Mathematics. Vol. 58, American Mathematical Society, 2000.

[4] Deza, Elena, and Michel Marie Deza. Encyclopedia of Distances, Springer Berlin Heidelberg, 2009.

拡張機能

自動並列サポート

Parallel Computing Toolbox™ を使用して自動的に並列計算を実行することで、コードを高速化します。

並列実行するには、この関数を呼び出すときに名前と値の引数 Options を指定し、statset を使用してオプション構造体の UseParallel フィールドを true に設定します。

Options=statset(UseParallel=true)

並列計算の詳細については、自動並列サポートを使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2022a で導入

参考

DriftDiagnostics | ecdf | histcounts | plotDriftStatus | plotEmpiricalCDF | plotHistogram | plotPermutationResults | summary