resubMargin
マルチクラス誤り訂正出力符号 (ECOC) モデルの再代入分類マージン
説明
m = resubMargin(Mdl,Name,Value)
例
SVM バイナリ学習器による ECOC モデルの再代入分類マージンを計算します。
フィッシャーのアヤメのデータ セットを読み込みます。予測子データ X と応答データ Y を指定します。
load fisheriris
X = meas;
Y = species;SVM バイナリ分類器を使用して ECOC モデルを学習させます。SVM テンプレートを使用して予測子を標準化し、クラスの順序を指定します。
t = templateSVM('Standardize',true);
classOrder = unique(Y)classOrder = 3×1 cell
{'setosa' }
{'versicolor'}
{'virginica' }
Mdl = fitcecoc(X,Y,'Learners',t,'ClassNames',classOrder);
t は SVM テンプレート オブジェクトです。学習時は、t の空のプロパティに対して既定値が使用されます。Mdl は ClassificationECOC モデルです。
Mdl の学習に使用した観測値の分類マージンを計算します。箱ひげ図を使用してマージンの分布を表示します。
m = resubMargin(Mdl);
boxplot(m)
title('In-Sample Margins')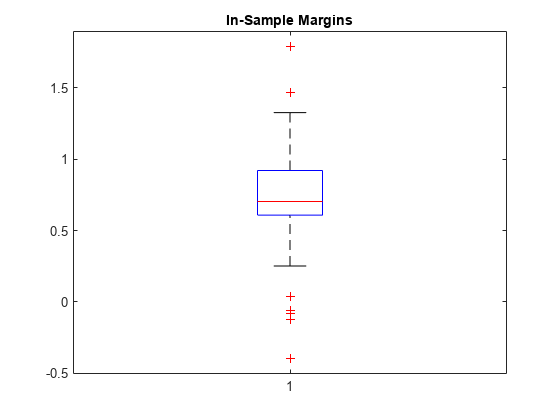
観測値の分類マージンは、符号を反転した陽性クラスの損失から符号を反転した陰性クラスの最大損失を減算した値です。マージンが比較的大きくなる分類器を選択します。
複数のモデルによる学習標本マージンを比較することにより、特徴選択を実行します。この比較のみに基づくと、マージンが最大である分類器が最適な分類器です。
フィッシャーのアヤメのデータ セットを読み込みます。次の 2 つのデータ セットを定義します。
fullXには 4 つすべての予測子が含まれます。partXにはがく片の測定値のみが含まれます。
load fisheriris
X = meas;
fullX = X;
partX = X(:,1:2);
Y = species;各予測子セットについて SVM バイナリ学習器を使用する ECOC モデルに学習をさせます。SVM テンプレートを使用して予測子を標準化し、クラスの順序を指定して、事後確率を計算します。
t = templateSVM('Standardize',true);
classOrder = unique(Y)classOrder = 3×1 cell
{'setosa' }
{'versicolor'}
{'virginica' }
FullMdl = fitcecoc(fullX,Y,'Learners',t,'ClassNames',classOrder,... 'FitPosterior',true); PartMdl = fitcecoc(partX,Y,'Learners',t,'ClassNames',classOrder,... 'FitPosterior',true);
各分類器の再代入マージンを計算します。モデルごとに箱ひげ図を使用してマージンの分布を表示します。
fullMargins = resubMargin(FullMdl); partMargins = resubMargin(PartMdl); boxplot([fullMargins partMargins],'Labels',{'All Predictors','Two Predictors'}) title('Training-Sample Margins')
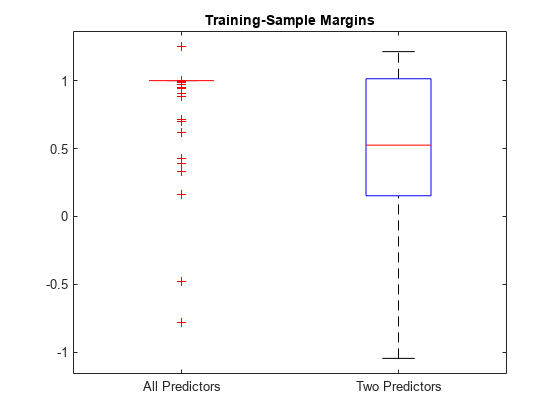
FullMdl のマージンの分布は、PartMdl のマージンの分布よりも高い位置にあり、変動性がより少なくなっています。この結果は、すべての予測子によって学習をさせたモデルの方が、学習データの当てはめが優れていることを示しています。
入力引数
学習済みの完全なマルチクラス ECOC モデル。fitcecoc によって学習をさせた ClassificationECOC モデルを指定します。
名前と値の引数
オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。
R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。
例: resubMargin(Mdl,'Verbose',1) は、診断メッセージをコマンド ウィンドウに表示するよう指定します。
バイナリ学習器損失関数。組み込みの損失関数の名前または関数ハンドルとして指定します。
次の表で、組み込み関数について説明します。ここで、yj は特定のバイナリ学習器のクラス ラベル (集合 {–1,1,0} 内)、sj は観測値 j のスコア、g(yj,sj) はバイナリ損失の式です。
値 説明 スコア領域 g(yj,sj) "binodeviance"二項分布からの逸脱度 (–∞,∞) log[1 + exp(–2yjsj)]/[2log(2)] "exponential"指数 (–∞,∞) exp(–yjsj)/2 "hamming"ハミング [0,1] または (–∞,∞) [1 – sign(yjsj)]/2 "hinge"ヒンジ (–∞,∞) max(0,1 – yjsj)/2 "linear"線形 (–∞,∞) (1 – yjsj)/2 "logit"ロジスティック (–∞,∞) log[1 + exp(–yjsj)]/[2log(2)] "quadratic"2 次 [0,1] [1 – yj(2sj – 1)]2/2 バイナリ損失は、yj = 0 の場合に損失が 0.5 になるように正規化されます。また、各クラスについて平均のバイナリ損失が計算されます[1]。
カスタム バイナリ損失関数の場合は関数ハンドルを指定します。たとえば、
customFunctionの場合はBinaryLoss=@customFunctionを指定します。customFunctionの形式は次のとおりです。bLoss = customFunction(M,s)
MはMdl.CodingMatrixに格納された K 行 B 列の符号化行列です。sは 1 行 B 列の分類スコアの行ベクトルです。bLossは分類損失です。このスカラーは、特定のクラスのすべての学習器についてバイナリ損失を集計します。たとえば、平均バイナリ損失を使用して、各クラスの学習器の損失を集計できます。K は、クラスの数です。
B はバイナリ学習器の数です。
カスタムなバイナリ損失関数を渡す例については、カスタム バイナリ損失関数の使用による ECOC モデルのテスト標本ラベルの予測を参照してください。
次の表に BinaryLoss の既定値を示します。既定値は、バイナリ学習器が返すスコアの範囲によって異なります。
| 仮定 | 既定値 |
|---|---|
すべてのバイナリ学習器が次のいずれかである。
| "quadratic" |
| すべてのバイナリ学習器が SVM であるか、SVM 学習器の線形またはカーネル分類モデルである。 | "hinge" |
すべてのバイナリ学習器が、AdaboostM1 または GentleBoost によって学習をさせたアンサンブルである。 | "exponential" |
すべてのバイナリ学習器が、LogitBoost によって学習をさせたアンサンブルである。 | "binodeviance" |
fitcecoc で FitPosterior=true を設定して、クラスの事後確率を予測するように指定している。 | "quadratic" |
| バイナリ学習器が異種混合で、さまざまな損失関数を使用している。 | "hamming" |
既定値を確認するには、コマンド ラインでドット表記を使用して学習済みモデルの BinaryLoss プロパティを表示します。
例: BinaryLoss="binodeviance"
データ型: char | string | function_handle
バイナリ損失を集計する復号化方式。"lossweighted" または "lossbased" として指定します。詳細は、バイナリ損失を参照してください。
例: Decoding="lossbased"
データ型: char | string
推定オプション。statset によって返される構造体配列として指定します。
並列計算を起動するには、Parallel Computing Toolbox™ ライセンスが必要です。
例: Options=statset(UseParallel=true)
データ型: struct
詳細レベル。0 または 1 として指定します。Verbose は、コマンド ウィンドウに表示される診断メッセージの量を制御します。
Verbose が 0 の場合、診断メッセージは表示されません。それ以外の場合は、診断メッセージが表示されます。
例: Verbose=1
データ型: single | double
詳細
"分類マージン" は、各観測値における真のクラスの負の損失と偽のクラスの負の最大損失の差です。各マージンのスケールが同じである場合、マージンを分類の信頼尺度として使用できます。複数の分類器の中で、マージンが大きい分類器の方が優れています。
"バイナリ損失" は、バイナリ学習器がどの程度の精度で観測値をクラスに分類するかを決定する、クラスと分類スコアの関数です。ソフトウェアでバイナリ損失をどのように集計して各観測値の予測クラスを判定するかは、ECOC モデルの "復号化方式" で指定します。
以下のように仮定します。
mkj は符号化設計行列 M の要素 (k,j)、つまりバイナリ学習器 j のクラス k に対応する符号。M は K 行 B 列の行列であり、K はクラスの数、B はバイナリ学習器の数です。
sj は観測値に対するバイナリ学習器 j のスコア。
g はバイナリ損失関数。
は観測値の予測クラス。
ソフトウェアでは 2 つの復号化方式をサポートしています。
関数 predict、resubPredict、および kfoldPredict は、それぞれの観測値とクラスについて、argmin の目的関数の符号反転値を 2 番目の出力引数 (NegLoss) として返します。
次の表は、サポートされる損失関数をまとめたものです。ここで、yj は特定のバイナリ学習器のクラス ラベル (集合 {–1,1,0} 内)、sj は観測値 j のスコア、g(yj,sj) はバイナリ損失関数です。
| 値 | 説明 | スコア領域 | g(yj,sj) |
|---|---|---|---|
"binodeviance" | 二項分布からの逸脱度 | (–∞,∞) | log[1 + exp(–2yjsj)]/[2log(2)] |
"exponential" | 指数 | (–∞,∞) | exp(–yjsj)/2 |
"hamming" | ハミング | [0,1] または (–∞,∞) | [1 – sign(yjsj)]/2 |
"hinge" | ヒンジ | (–∞,∞) | max(0,1 – yjsj)/2 |
"linear" | 線形 | (–∞,∞) | (1 – yjsj)/2 |
"logit" | ロジスティック | (–∞,∞) | log[1 + exp(–yjsj)]/[2log(2)] |
"quadratic" | 2 次 | [0,1] | [1 – yj(2sj – 1)]2/2 |
yj = 0 のときに損失が 0.5 になるようにバイナリ損失が正規化され、バイナリ学習器の平均が集計に使用されます[1]。
ECOC 分類器の全体的な性能の尺度である全体の分類損失 (オブジェクト関数 resubLoss および resubPredict の名前と値の引数 LossFun により指定) とバイナリ損失を混同しないでください。
ヒント
複数の ECOC 分類器のマージンまたはエッジを比較するには、テンプレート オブジェクトを使用して分類器間で共通するスコア変換関数を学習時に指定します。
参照
[1] Allwein, E., R. Schapire, and Y. Singer. “Reducing multiclass to binary: A unifying approach for margin classifiers.” Journal of Machine Learning Research. Vol. 1, 2000, pp. 113–141.
[2] Escalera, S., O. Pujol, and P. Radeva. “Separability of ternary codes for sparse designs of error-correcting output codes.” Pattern Recog. Lett. Vol. 30, Issue 3, 2009, pp. 285–297.
[3] Escalera, S., O. Pujol, and P. Radeva. “On the decoding process in ternary error-correcting output codes.” IEEE Transactions on Pattern Analysis and Machine Intelligence. Vol. 32, Issue 7, 2010, pp. 120–134.
拡張機能
並列実行するには、この関数を呼び出すときに名前と値の引数 Options を指定し、statset を使用してオプション構造体の UseParallel フィールドを true に設定します。
Options=statset(UseParallel=true)
並列計算の詳細については、自動並列サポートを使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。
この関数は、GPU 配列を完全にサポートします。詳細は、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。
バージョン履歴
R2014b で導入
参考
ClassificationECOC | resubEdge | margin | predict | resubPredict | fitcecoc | resubLoss
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Web サイトの選択
Web サイトを選択すると、翻訳されたコンテンツにアクセスし、地域のイベントやサービスを確認できます。現在の位置情報に基づき、次のサイトの選択を推奨します:
また、以下のリストから Web サイトを選択することもできます。
最適なサイトパフォーマンスの取得方法
中国のサイト (中国語または英語) を選択することで、最適なサイトパフォーマンスが得られます。その他の国の MathWorks のサイトは、お客様の地域からのアクセスが最適化されていません。
南北アメリカ
- América Latina (Español)
- Canada (English)
- United States (English)
ヨーロッパ
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)