このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

PID コントローラーに対する制約の適用

以下の例では、Constraint Enforcement ブロックを使用して、既知の制約を PID 制御アプリケーションに適用する方法を説明します。

概要

この例では、プラント ダイナミクスは次の方程式 [1] で記述されます。

$$\begin{array}{l}{\underset{}{\overset{\dot{}}{x}}}_1=-x_1+(x_1^2+1)u_1\\ {\underset{}{\overset{\dot{}}{x}}}_2=-x_2+(x_2^2+1)u_2\end{array}$$

プラントの目標は、次のように定義された望ましい軌跡を追従することです。

$$\begin{array}{l}\underset{}{\overset{\dot{}}{\theta }}=0.1\pi \\ {\underset{}{\overset{\dot{}}{x}}}_{1d}=-r\cos (\theta )\\ {\underset{}{\overset{\dot{}}{x}}}_{2d}=r\sin (\theta )\end{array}$$

同じ PID 制御アプリケーションに対して、既知の制約関数を学習し、適用する例については、PID コントローラーの制約の学習と適用を参照してください。

モデル パラメーターと初期状態を設定します。

r = 1.5;   % Radius for desired trajectory
Ts = 0.1;  % Sample time
Tf = 22;   % Duration
x0_1 = -r; % Initial condition for x1
x0_2 = 0;  % Initial condition for x2

PID コントローラーの設計

制約を適用する前に、基準軌跡を追従するための PID コントローラーを設計します。trackingWithPIDs モデルには、PID 調整器アプリを使用して調整されたゲインをもつ 2 つの PID コントローラーが含まれています。Simulink モデルにおける PID コントローラーの調整の詳細については、Simulink でのモデルベースの PID 調整の紹介を参照してください。

mdl = 'trackingWithPIDs';
open_system(mdl)

PID コントローラーをシミュレートし、追従性能をプロットします。

% Simulate the model.
out = sim(mdl);

% Extract trajectories.
logData = out.logsout;
x1_traj = logData{3}.Values.Data;
x2_traj = logData{4}.Values.Data;
x1_des = logData{1}.Values.Data;
x2_des = logData{2}.Values.Data;

% Plot trajectories.
figure('Name','Tracking')
xlim([-2,2])
ylim([-2,2])
plot(x1_des,x2_des,'r')
xlabel('x1')
ylabel('x2')
hold on
plot(x1_traj,x2_traj,'b:','LineWidth',2)
hold on
plot(x1_traj(1),x2_traj(1),'g*')
hold on
plot(x1_traj(end),x2_traj(end),'go')
legend('Desired','Trajectory','Start','end')

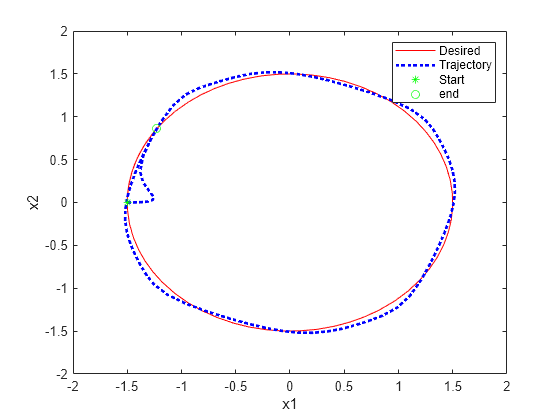
制約関数

この例では、Constraint Enforcement ブロックを使用して、既知の制約をアプリケーションに適用します。このブロックは、制約関数を満たすように制御動作を調整します。

この例では、プラントの実行可能領域は、$\left\{\mathit{x}:{\mathit{x}}_1\le 1,{\mathit{x}}_{\mathit{x}}\le 1\right\}$ で与えられます。したがって、プラントの次状態の条件 ${\mathit{x}}_{\mathit{k}+1}=\left[\begin{array}{c}{\mathit{x}}_1\left(\mathit{k}+1\right)\\ {\mathit{x}}_2\left(\mathit{k}+1\right)\end{array}\right]$ は ${\mathit{x}}_{\mathit{k}+1}\le \left[\begin{array}{c}1\\ 1\end{array}\right]$ を満たさなければなりません。

プラント ダイナミクスを次の方程式で近似できます。

${\mathit{x}}_{\mathit{k}+1}\approx \left[\begin{array}{cc}\left(1-{\mathit{T}}_{\mathit{s}}\right)& 0\\ 0& \left(1-{\mathit{T}}_{\mathit{s}}\right)\end{array}\right]{\mathit{x}}_{\mathit{k}}+\left[\begin{array}{cc}{\mathit{T}}_{\mathit{s}}\left(1+{\mathit{x}}_1^2\left(\mathit{k}\right)\right)& 0\\ 0& {\mathit{T}}_{\mathit{s}}\left(1+{\mathit{x}}_2^2\left(\mathit{k}\right)\right)\end{array}\right]{\mathit{u}}_{\mathit{k}}$

制約をこの方程式に適用すると、以下の制約関数が生成されます。

$\left[\begin{array}{cc}\left(1-{\mathit{T}}_{\mathit{s}}\right)& 0\\ 0& \left(1-{\mathit{T}}_{\mathit{s}}\right)\end{array}\right]{\mathit{x}}_{\mathit{k}}+\left[\begin{array}{cc}{\mathit{T}}_{\mathit{s}}\left(1+{\mathit{x}}_1^2\left(\mathit{k}\right)\right)& 0\\ 0& {\mathit{T}}_{\mathit{s}}\left(1+{\mathit{x}}_2^2\left(\mathit{k}\right)\right)\end{array}\right]{\mathit{u}}_{\mathit{k}}\le \left[\begin{array}{c}1\\ 1\end{array}\right]$

Constraint Enforcement ブロックは、形式 ${\mathit{f}}_{\mathit{x}}+{\mathit{g}}_{\mathit{x}}\mathit{u}\le \mathit{c}$ の制約を受け入れます。このアプリケーションの場合、この制約関数の係数は以下のとおりです。

$${\mathit{f}}_{\mathit{x}}=\left[\begin{array}{cc}\left(1-{\mathit{T}}_{\mathit{s}}\right)& 0\\ 0& \left(1-{\mathit{T}}_{\mathit{s}}\right)\end{array}\right]{\mathit{x}}_{\mathit{k}},{\mathit{g}}_{\mathit{x}}=\left[\begin{array}{cc}{\mathit{T}}_{\mathit{s}}\left(1+{\mathit{x}}_1^2\left(\mathit{k}\right)\right)& 0\\ 0& {\mathit{T}}_{\mathit{s}}\left(1+{\mathit{x}}_2^2\left(\mathit{k}\right)\right)\end{array}\right],\mathit{c}=\left[\begin{array}{c}1\\ 1\end{array}\right]$$

Constraint Enforcement を使用した PID コントローラーのシミュレーション

trackingWithConstraintPID モデルには、PID コントローラー、プラント ダイナミクス、および制約の実装が含まれています。

mdl = 'trackingWithKnownConstraintPID';
open_system(mdl)

制約の実装を表示するには、Constraint サブシステムを開きます。ここで、モデルは MATLAB Function ブロックを使用して既知の制約関数を実装しており、Constraint Enforcement ブロックにより制約関数が適用されます。

モデルを実行し、シミュレーション結果をプロットします。このプロットから、プラントの状態が 1 より小さいことがわかります。

% Simulate the model.
out = sim(mdl);

% Extract trajectories.
logData = out.logsout;
x1_traj = zeros(size(out.tout));
x2_traj = zeros(size(out.tout));
for ct = 1:size(out.tout,1)
    x1_traj(ct) = logData{4}.Values.Data(:,:,ct);
    x2_traj(ct) = logData{5}.Values.Data(:,:,ct);
end

x1_des = logData{2}.Values.Data;
x2_des = logData{3}.Values.Data;

% Plot trajectories.
figure('Name','Tracking with Constraint');
plot(x1_des,x2_des,'r')
xlabel('x1')
ylabel('x2')
hold on
plot(x1_traj,x2_traj,'b:','LineWidth',2)
hold on
plot(x1_traj(1),x2_traj(1),'g*')
hold on
plot(x1_traj(end),x2_traj(end),'go')
legend('Desired','Trajectory','Start','End','Location','best')

Constraint Enforcement ブロックによって、プラントが 1 より小さい状態を維持するように、正常に制御動作が制約されています。

bdclose('trackingWithPIDs')
bdclose('trackingWithKnownConstraintPID')

参考文献

[1] Robey, Alexander, Haimin Hu, Lars Lindemann, Hanwen Zhang, Dimos V. Dimarogonas, Stephen Tu, and Nikolai Matni. "Learning Control Barrier Functions from Expert Demonstrations." Preprint, submitted April 7, 2020. https://arxiv.org/abs/2004.03315

参考

ブロック

• Constraint Enforcement

アプリ

• PID 調整器

関連するトピック

• 制御設計への制約の適用
• PID コントローラーの制約の学習と適用
• 制約の適用を使用した強化学習エージェントの学習
• Simulink でのモデルベースの PID 調整の紹介