besself

ベッセル アナログ フィルターの設計

ページ内をすべて折りたたむ

構文

[b,a] = besself(n,Wo)
[z,p,k] = besself(___)
[A,B,C,D] = besself(___)

説明

[b,a] = besself(n,Wo) は、n 次ローパス アナログ ベッセル フィルターの伝達関数係数を返します。ここで、Wo はフィルターの群遅延が近似的に定数になる角周波数です。n の値が大きくなるに従って、定数が Wo を上限としてより良く近似される群遅延が生成されます。関数 besself は、デジタル ベッセル フィルターの設計をサポートしません。

例

[z,p,k] = besself(___) はローパスのアナログ ベッセル フィルターを設計し、その零点、極、およびゲインを返します。

例

[A,B,C,D] = besself(___) はアナログ ベッセル フィルターを設計し、その状態空間表現を指定する行列を返します。

例

すべて折りたたむ

ライブ スクリプトを開く

最大 104 ラジアン/秒の定数近似群遅延を持つ 5 次のアナログ ローパス ベッセル フィルターを設計します。freqs を使用してフィルターの振幅応答および位相応答をプロットします。

wc = 10000;
[b,a] = besself(5,wc);
freqs(b,a)

Figure contains 2 axes objects. Axes object 1 with xlabel Frequency (rad/s), ylabel Phase (degrees) contains an object of type line. Axes object 2 with xlabel Frequency (rad/s), ylabel Magnitude contains an object of type line.

フィルターの群遅延応答を、アンラップされた位相応答の微分の負として計算します。カットオフ周波数までの範囲で近似的に定数であることを検証するために群遅延をプロットします。

[h,w] = freqs(b,a);
grpdel = -diff(unwrap(angle(h)))./diff(w);

clf
loglog(w(2:end),grpdel)
xlabel("Frequency (rad/s)")
ylabel("Group delay (s)")
xline(wc)
grid on

Figure contains an axes object. The axes object with xlabel Frequency (rad/s), ylabel Group delay (s) contains 2 objects of type line, constantline.

ライブ スクリプトを開く

アナログ フィルターと同等の、最大限に平坦な群遅延をもつ 4 次デジタル IIR フィルターを設計します。

カットオフ周波数が 300 Hz のアナログ ローパス 4 次ベッセル フィルターを設計します。

[b,a] = besself(4,2*pi*300);

インパルス不変法を使用して、アナログ フィルターからデジタル フィルターに変換します。サンプル レートは 1000 Hz です。

Fs = 10000;
[bd,ad] = impinvar(b,a,Fs);

アナログおよびデジタルのベッセル フィルターの周波数応答と群遅延を計算します。1 Hz から 1 kHz の間に幾何学的に分散された 2048 個の周波数点を指定します。群遅延応答をプロットします。どちらの設計も同じ結果になります。

f = logspace(1,3,2048);

HfAnalog = freqs(b,a,2*pi*f);
HfDigital = freqz(bd,ad,2*pi*f/Fs);
gdAnalog = -diff(unwrap(angle(HfAnalog)))./diff(2*pi*f);
gdDigital = -diff(unwrap(angle(HfDigital)))./diff(2*pi*f);

semilogx(f(2:end),gdAnalog,"-",f(2:end),gdDigital,"--")
xlabel("Frequency (Hz)")
ylabel("Group delay (sec)")
legend(["Analog","  Digital"])
grid on

Figure contains an axes object. The axes object with xlabel Frequency (Hz), ylabel Group delay (sec) contains 2 objects of type line. These objects represent Analog, Digital.

ライブ スクリプトを開く

カットオフ周波数が 2 GHz である 5 次のアナログ バタワース ローパス フィルターを設計します。2π 倍にして周波数を秒あたりのラジアン単位に変換します。4096 点でのフィルターの周波数応答を計算します。

n = 5;
wc = 2*pi*2e9;
w = 2*pi*1e9*logspace(-2,1,4096)';

[zb,pb,kb] = butter(n,wc,"s");
[bb,ab] = zp2tf(zb,pb,kb);
[hb,wb] = freqs(bb,ab,w);
gdb = -diff(unwrap(angle(hb)))./diff(wb);

エッジ周波数が同じで、通過帯域リップルが 3 dB である 5 次のチェビシェフ I 型フィルターを設計します。その周波数応答を計算します。

[z1,p1,k1] = cheby1(n,3,wc,"s");
[b1,a1] = zp2tf(z1,p1,k1);
[h1,w1] = freqs(b1,a1,w);
gd1 = -diff(unwrap(angle(h1)))./diff(w1);

エッジ周波数が同じで、阻止帯域の減衰量が 30 dB である 5 次のチェビシェフ II 型フィルターを設計します。その周波数応答を計算します。

[z2,p2,k2] = cheby2(n,30,wc,"s");
[b2,a2] = zp2tf(z2,p2,k2);
[h2,w2] = freqs(b2,a2,w);
gd2 = -diff(unwrap(angle(h2)))./diff(w2);

エッジ周波数が同じで、通過帯域リップルが 3 dB、阻止帯域の減衰量が 30 dB である 5 次の楕円フィルターを設計します。その周波数応答を計算します。

[ze,pe,ke] = ellip(n,3,30,wc,"s");
[be,ae] = zp2tf(ze,pe,ke);
[he,we] = freqs(be,ae,w);
gde = -diff(unwrap(angle(he)))./diff(we);

エッジ周波数が同じである 5 次のベッセル フィルターを設計します。その周波数応答を計算します。

[zf,pf,kf] = besself(n,wc);
[bf,af] = zp2tf(zf,pf,kf);
[hf,wf] = freqs(bf,af,w);
gdf = -diff(unwrap(angle(hf)))./diff(wf);

減衰をデシベルでプロットします。周波数をギガヘルツで表します。フィルターを比較します。

fGHz = [wb w1 w2 we wf]/(2e9*pi);
plot(fGHz,mag2db(abs([hb h1 h2 he hf])))
axis([0 5 -45 5])
grid on
xlabel("Frequency (GHz)")
ylabel("Attenuation (dB)")
legend(["butter" "cheby1" "cheby2" "ellip" "besself"])

Figure contains an axes object. The axes object with xlabel Frequency (GHz), ylabel Attenuation (dB) contains 5 objects of type line. These objects represent butter, cheby1, cheby2, ellip, besself.

サンプル単位で群遅延をプロットします。周波数をギガヘルツで、群遅延をナノ秒で表します。フィルターを比較します。

gdns = [gdb gd1 gd2 gde gdf]*1e9;
gdns(gdns<0) = NaN;
loglog(fGHz(2:end,:),gdns)
grid on
xlabel("Frequency (GHz)")
ylabel("Group delay (ns)")
legend(["butter" "cheby1" "cheby2" "ellip" "besself"])

Figure contains an axes object. The axes object with xlabel Frequency (GHz), ylabel Group delay (ns) contains 5 objects of type line. These objects represent butter, cheby1, cheby2, ellip, besself.

バタワース フィルターおよびチェビシェフ II 型フィルターには平坦な通過帯域と広い遷移帯域幅があります。チェビシェフ I 型フィルターおよび楕円フィルターは速くロールオフしますが、通過帯域リップルがあります。チェビシェフ II 型設計関数に対する周波数入力は、通過帯域の末尾ではなく阻止帯域の始点を設定します。ベッセル フィルターは、通過帯域に沿って定数近似群遅延をもちます。

入力引数

すべて折りたたむ

フィルター次数。25 以下の整数スカラーとして指定します。バンドパスおよびバンドストップの設計では、n がフィルター次数の 1/2 を表します。

データ型: double

カットオフ周波数。正のスカラーとして指定します。カットオフ周波数は、フィルターの群遅延が近似的に定数になる周波数範囲の上限および下限です。カットオフ周波数はラジアン/秒で表します。

データ型: double

出力引数

すべて折りたたむ

フィルターの伝達関数の係数。ローパス フィルターおよびハイパス フィルターの場合は長さ n + 1 の行ベクトルとして、バンドパス フィルターおよびバンドストップ フィルターの場合は長さ 2n + 1 の行ベクトルとして返されます。b と a によるこの伝達関数式は次になります。

H(s)=b1 sr−1+b2 sr−2+⋯+bra1 sr−1+a2 sr−2+⋯+ar

データ型: double

フィルターのゼロ、極、ゲイン。長さ n (バンドパス設計とバンドストップ設計の場合は 2n) およびスカラーの 2 つの列ベクトルとして返されます。z、p および k によるこの伝達関数式は次になります。

H(s)=k(s−z1) (s−z2)⋯(s−zr)(s−p1) (s−p2)⋯(s−pr)

データ型: double

フィルターの状態空間表現。行列として返されます。ローパス設計とハイパス設計の場合、m = n で、バンドパス フィルターとバンドストップ フィルターの場合に m = 2n ならば、A は m × m で、B は m × 1、C は 1 × m、D は 1 × 1 となります。

状態空間の行列は状態ベクトル x、入力 u、出力 y を以下の式により表します。

x˙=A x+B uy=C x+D u.

データ型: double

アルゴリズム

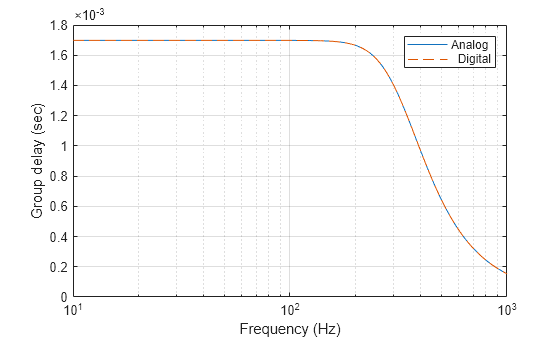
関数 besself は、アナログ ベッセル フィルターを設計します。このフィルターは、通過帯域全体でほぼ一定の群遅延をもつという特徴をもち、したがってフィルター処理後の信号波形を通過帯域で保持しています。

ローパス ベッセル フィルターの振幅応答は、ローパス バタワース フィルターと同様、単調減少します。バタワース、チェビシェフ、および楕円の各フィルターに比べ、ベッセル フィルターは最も緩やかなロールオフをもち、減衰仕様を満たすために最も高い次数を必要とします。

高次フィルターにおいては、状態空間形式が数値的に最も正確であり、零点-極-ゲイン形式がこれに続きます。伝達関数係数形式は最も精度が劣り、15 次程度の低さのフィルター次数でも数値的な問題が生じる可能性があります。

besself は、以下の 4 つの手順のアルゴリズムを使用します。

  1. 関数besselapを使用して、ローパス アナログ プロトタイプの極、零点、およびゲインを求めます。

  2. 極、零点、およびゲインを状態空間形式に変換します。

  3. 関数 lp2lp を使用して、連続時間状態空間ローパス フィルターのプロトタイプを、指定されたカットオフ周波数をもつローパス フィルターに変換します。

  4. 必要に応じて、状態空間フィルターを伝達関数、または、零点-極-ゲイン形式に逆変換します。

参照

[1] Parks, Thomas W., and C. Sidney Burrus. Digital Filter Design. New York: John Wiley & Sons, 1987.

バージョン履歴

R2006a より前に導入

参考

| | | |