inverseKinematics
逆運動学ソルバーの作成
説明
inverseKinematics System object™ は、指定された剛体ツリー モデルに基づいて目的のエンドエフェクタ姿勢のジョイント コンフィギュレーションを計算するための、逆運動学 (IK) ソルバーを作成します。rigidBodyTree クラスを使用して、ロボットの剛体ツリー モデルを作成します。このモデルは、ソルバーが強制するすべてのジョイント拘束を定義します。求解が可能な場合、ロボット モデルで指定されているジョイント制限に従います。
IK ソルバーは、勾配降下法ベースの最適化アプローチを使用して、重み付き姿勢誤差二乗の目的関数の局所的最小値となるジョイント コンフィギュレーションを見つけます。
ここで、
w は 6 要素の重みベクトルです。
weights引数を使用してこれを指定すると、向き成分と並進成分との間の相対的な重要度の優先順位を設定できます。は、目的のエンドエフェクタ姿勢 Tdes と順運動学で計算されたエンドエフェクタ姿勢との間の 6 要素の姿勢誤差を表すベクトル値関数です。
FK は、ロボットのエンドエフェクタ リンク ee_link について、ジョイント コンフィギュレーション q における姿勢を計算する順運動学関数です。
照準拘束、位置の範囲、方向ターゲットなど、エンドエフェクタ姿勢以外の拘束をさらに指定するには、generalizedInverseKinematics の使用を検討してください。このオブジェクトにより、複数拘束の IK の解を計算できます。
IK の閉形式解析解の詳細については、analyticalInverseKinematics を参照してください。
目的のエンドエフェクタ姿勢に対するジョイント コンフィギュレーションを計算するには、以下を実行します。
inverseKinematicsオブジェクトを作成して、そのプロパティを設定します。関数と同様に、引数を指定してオブジェクトを呼び出します。
System object の機能の詳細については、System object とはを参照してください。
作成
説明
ik = inverseKinematicsRigidBodyTree プロパティで剛体ツリーモデルを指定します。
ik = inverseKinematics(PropertyName=Value)SolverAlgorithm="fminconsqp" は逆運動学ソルバーとして fmincon SQP ソルバーを使用します。
プロパティ
使用法
説明
[ は、指定したエンドエフェクタ姿勢を達成するジョイント コンフィギュレーションを探します。コンフィギュレーションの初期推定と、configSol,solInfo] = ik(endeffector,pose,weights,initialguess)pose の 6 成分に対する許容誤差の重みの目標値を指定します。アルゴリズムの実行に関連する解の情報 solInfo が、ジョイント コンフィギュレーションの解 configSol とともに返されます。
入力引数
出力引数
オブジェクト関数
オブジェクト関数を使用するには、System object を最初の入力引数として指定します。たとえば、obj という名前の System object のシステム リソースを解放するには、以下の構文を使用します。
release(obj)
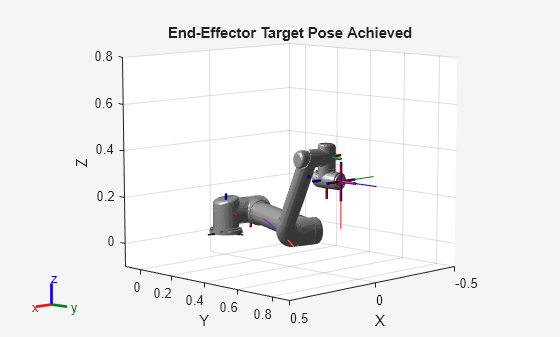
例
Robotics System Toolbox™ loadrobotから PUMA 560 マニピュレーターを読み込みます。
puma = loadrobot("puma560");目的のエンドエフェクタ位置を設定し、SE(3) 同次変換行列に変換します。
pos = [-0.5 0.5 0.75]; eePoseTF = trvec2tform(pos);
IK ソルバーを作成し、ソルバーが目的の向きよりも目的の xyz 位置への到達を優先するように重みを設定します。ソルバーの初期推定として、ホーム ジョイント コンフィギュレーションを使用します。
ik = inverseKinematics("RigidBodyTree",puma);
weights = [0 0 0 1 1 1];
initialguess = homeConfiguration(puma);ロボット モデル link7 について、エンドエフェクタの IK を解きます。
[configSoln,solnInfo] = ik("link7",eePoseTF,weights,initialguess);生成された解のコンフィギュレーションを表示します。これでゴール位置に到達しました。
show(puma,configSoln); hold on plotTransforms(pos,eul2quat([0 0 0]),FrameSize=0.3); axis auto padded title("End-Effector Target Position Achieved")
ほとんどの IK 問題では、目的の姿勢ターゲットに到達できるコンフィギュレーションが複数あることに注意してください。ソルバーは最適化ベースであるため、目的の姿勢に実際には到達しない解に近づくことがあります。これが発生した場合、ソルバーは自動的に再起動し、ランダムなコンフィギュレーションを初期推定として使用します。つまり、同じ姿勢ターゲットに対して関数を複数回実行すると、すべてが姿勢ターゲットに到達する異なるコンフィギュレーションが得られることがあります。ランダム性を回避するには、乱数発生器のシードを設定するか、AllowRandomRestart を無効にするとともに、解に近い初期推定を使用することができます。
ik.SolverParameters.AllowRandomRestart = false
可能なすべての解を求める必要がある場合は、analyticalInverseKinematicsオブジェクトを使用します。
ロボットを読み込み、その逆運動学ソルバーを作成します。ソルバーのアルゴリズムを fmincon SQP アルゴリズムに設定します。
robot = loadrobot("universalUR5",DataFormat="row"); ik = inverseKinematics(RigidBodyTree=robot,SolverAlgorithm="fminconsqp");
ロボットの最後のボディをエンドエフェクタとして設定し、ターゲット姿勢、重み、初期推定コンフィギュレーションを設定します。
ee = robot.BodyNames{end};
poseTarget = se3([0 pi/2 -pi/2],"eul","ZYX",[0 0.7 0.3]);
weights = [1 1 1 0.8 0.8 0.8];
initGuessConfig = [pi/2 0 0 0 0 0];初期推定コンフィギュレーションのロボットを表示し、ターゲット姿勢をプロットします。
show(robot,initGuessConfig); axis([-0.5 0.5 -0.1 0.9 -0.1 0.8]) hold on plotTransforms(poseTarget,FrameSize=0.2); title("Initial Guess Configuration and Pose Target")
指定した重みと初期推定コンフィギュレーションを使用して、姿勢ターゲットに達するコンフィギュレーションを求めます。
[config,solninfo] = ik(ee,tform(poseTarget),weights,initGuessConfig); show(robot,config,PreservePlot=false); title("End-Effector Target Pose Achieved") hold off
solninfo.Status
ans = 'success'
参照
[1] Badreddine, Hassan, Stefan Vandewalle, and Johan Meyers. "Sequential Quadratic Programming (SQP) for Optimal Control in Direct Numerical Simulation of Turbulent Flow." Journal of Computational Physics. 256 (2014): 1–16. doi:10.1016/j.jcp.2013.08.044.
[2] Bertsekas, Dimitri P. Nonlinear Programming. Belmont, MA: Athena Scientific, 1999.
[3] Goldfarb, Donald. "Extension of Davidon’s Variable Metric Method to Maximization Under Linear Inequality and Equality Constraints." SIAM Journal on Applied Mathematics. Vol. 17, No. 4 (1969): 739–64. doi:10.1137/0117067.
[4] Nocedal, Jorge, and Stephen Wright. Numerical Optimization. New York, NY: Springer, 2006.
[5] Sugihara, Tomomichi. "Solvability-Unconcerned Inverse Kinematics by the Levenberg–Marquardt Method." IEEE Transactions on Robotics Vol. 27, No. 5 (2011): 984–91. doi:10.1109/tro.2011.2148230.
[6] Zhao, Jianmin, and Norman I. Badler. "Inverse Kinematics Positioning Using Nonlinear Programming for Highly Articulated Figures." ACM Transactions on Graphics Vol. 13, No. 4 (1994): 313–36. doi:10.1145/195826.195827.
