rlVectorQValueFunction
Vector Q-value function approximator with hybrid or discrete action space for reinforcement learning agents
Since R2022a
Description
This object implements a vector (also referred to as multi-output) Q-value
function approximator that you can use as a critic with a hybrid or discrete action space for
a reinforcement learning agent. A vector Q-value function (also known as vector action-value
function) is a mapping between a pair consisting of an observation and a continuous action to
a vector in which each element represents the expected discounted cumulative long-term reward
when an agent executes the discrete action corresponding to the specific
output number as well as the continuous action (if present) given as additional input,
starting from the state corresponding to the observation (also given in input), and follows a
given policy afterwards. A vector Q-value function critic for discrete action spaces therefore
needs only the observation as input (as there is no continuous action). After you create an
rlVectorQValueFunction critic, use it to create an agent such as rlQAgent, rlDQNAgent, rlSARSAAgent or an
hybrid rlSACAgent. For more
information on creating actors and critics, see Create Policies and Value Functions.
Creation
Syntax
Description
critic = rlVectorQValueFunction(net,observationInfo,actionInfo)critic with a
discrete or hybrid action space. Here,
net is the deep neural network used as an approximation model.
Its input layers must take in all the observation channels as well as and the continuous
action channel (if present). The output layer must have as many elements as the number
of possible discrete actions. When you use this syntax, the network input layers are
automatically associated with the environment observation channels (and, if present, the
continuous action channel) according to the dimensions specified in
observationInfo (and if present, to the second action channel
specified in actionInfo). This function sets the
ObservationInfo and ActionInfo properties of
critic to the observationInfo and
actionInfo input arguments, respectively.
critic = rlVectorQValueFunction({basisFcn,W0},observationInfo,actionInfo)critic with a
discrete or hybrid action space using a
custom basis function as underlying approximation model. The first input argument is a
two-element cell array whose first element is the handle basisFcn
to a custom basis function and whose second element is the initial weight matrix
W0. Here the basis function must take in all the observation
channels as well as and the continuous action channel (if present), and
W0 must have as many columns as the number of possible discrete
actions. The function sets the ObservationInfo and ActionInfo properties of critic to the input
arguments observationInfo and actionInfo,
respectively.
critic = rlVectorQValueFunction(___,Name=Value)UseDevice property using one or more name-value arguments.
Specifying the input layer names (and, for hybrid action spaces, the continuous action
layer name) allows you explicitly associate the layers of your network approximator with
specific environment channels. For all types of approximators, you can specify the
device where computations for critic are executed, for example
UseDevice="gpu".
Input Arguments
Deep neural network used as the underlying approximator within the critic, specified as one of the following:
Array of
LayerobjectslayerGraphobjectDAGNetworkobjectSeriesNetworkobjectdlnetworkobject
Note
Among the different network representation options, dlnetwork is preferred, since it
has built-in validation checks and supports automatic differentiation. If you pass
another network object as an input argument, it is internally converted to a
dlnetwork object. However, best practice is to convert other
representations to dlnetwork explicitly before
using them to create a critic or an actor for a reinforcement learning agent. You can
do so using dlnet=dlnetwork(net), where net is
any Deep Learning Toolbox™ neural network object. The resulting dlnet is the
dlnetwork object that you use for your critic or actor. This
practice allows a greater level of insight and control for cases in which the
conversion is not straightforward and might require additional
specifications.
The network must have as many input layers as the number of environment observation channels (plus one for hybrid action spaces). Specifically, there must be one input layer for each observation channel, and one additional input layer for the continuous action channel, if present. The output layer must have as many elements as the number of possible discrete actions. Each element of the output approximates the value of executing the corresponding discrete action starting from the current observation when also executing the continuous observation given as input (if present).
rlQValueFunction objects support recurrent deep neural
networks.
The learnable parameters of the critic are the weights of the deep neural network. For a list of deep neural network layers, see List of Deep Learning Layers. For more information on creating deep neural networks for reinforcement learning, see Create Policies and Value Functions.
Custom basis function, specified as a function handle to a user-defined
MATLAB® function. The user defined function can either be an anonymous function
or a function on the MATLAB path. The output of the critic is the vector c =
W'*B, where W is a matrix containing the learnable
parameters, and B is the column vector returned by the custom basis
function. Each element of c approximates the value of executing the
corresponding discrete action starting from the current observation when also
executing the continuous observation given as input (if present).
Your basis function must have the following signature.
B = myBasisFunction(obs1,obs2,...,obsN,actC)
Here, obs1 to obsN are inputs in the same
order and with the same data type and dimensions as the channels defined in
observationInfo. For hybrid action spaces, the additional input
actC must have the same data type and dimension as the continuous
action channel defined in the second element of
actionInfo.
Example: @(obs1,obs2) [act(2)*obs1(1)^2;
abs(obs2(5))]
Initial value of the basis function weights W, specified as a
matrix having as many rows as the length of the basis function output vector and as
many columns as the number of possible discrete actions.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: UseDevice="gpu"
Network input layers names corresponding to the environment observation channels,
specified as a string array or a cell array of strings or character vectors. The
function assigns, in sequential order, each environment observation channel specified in
observationInfo to each layer whose name is specified in the
array assigned to this argument. Therefore, the specified network input layers, ordered
as indicated in this argument, must have the same data type and dimensions as the
observation channels, as ordered in observationInfo.
This name-value argument is supported only when the approximation model is a deep neural network.
Example: ObservationInputNames={"obsInLyr1_airspeed","obsInLyr2_altitude"}
Network input layer name corresponding to the environment continuous action
channel, specified as a string array or a cell array of character vectors. When the
action space has a continuous component, the function assigns the environment
continuous action channel specified in the second element of
actionInfo to the network input layer whose name is specified
in the value assigned to this argument. Therefore, the specified network input layer
must have the same data type and dimension as the continuous action channel defined
in the second element of actionInfo.
This name-value argument is supported only when the approximation model is a deep neural network and when the action space is hybrid.
Example: ContinuousActionInputName="actCInLyr_Temperature"
Properties
Observation specifications, specified as an rlFiniteSetSpec
or rlNumericSpec
object or an array containing a mix of such objects. Each element in the array defines
the properties of an environment observation channel, such as its dimensions, data type,
and name.
When you create the approximator object, the constructor function sets the
ObservationInfo property to the input argument
observationInfo.
You can extract observationInfo from an existing environment,
function approximator, or agent using getObservationInfo. You can also construct the specifications manually
using rlFiniteSetSpec
or rlNumericSpec.
Example: [rlNumericSpec([2 1])
rlFiniteSetSpec([3,5,7])]
Action specification, specified as a vector consisting of one rlFiniteSetSpec
followed by one rlNumericSpec
object. The action specification defines the properties of an environment action
channel, such as its dimensions, data type, and name.
Note
For hybrid action spaces, you must have two action channels, the first one for the discrete part of the action, the second one for the continuous part of the action.
When you create the approximator object, the constructor function sets the
ActionInfo property to the input argument
actionInfo.
You can extract ActionInfo from an existing environment or agent
using getActionInfo. You can also construct the specifications manually using
rlFiniteSetSpec
and rlNumericSpec.
Example: [rlFiniteSetSpec([-1 0 1]) rlNumericSpec([2
1])]
Action specifications, specified as an rlFiniteSetSpec
object. This object defines the properties of the environment action channel, such as
its dimensions, data type, and name.
Note
For this approximator object, only one action channel is allowed.
When you create the approximator object, the constructor function sets the
ActionInfo property to the input argument
actionInfo.
You can extract ActionInfo from an existing environment,
approximator object, or agent using getActionInfo. You can also construct the specification manually using
rlFiniteSetSpec.
Example: rlFiniteSetSpec([-1 0 1])
Normalization method, returned as an array in which each element (one for each input
channel defined in the observationInfo and
actionInfo properties, in that order) is one of the following
values:
"none"— Do not normalize the input."rescale-zero-one"— Normalize the input by rescaling it to the interval between 0 and 1. The normalized input Y is (U–Min)./(UpperLimit–LowerLimit), where U is the nonnormalized input. Note that nonnormalized input values lower thanLowerLimitresult in normalized values lower than 0. Similarly, nonnormalized input values higher thanUpperLimitresult in normalized values higher than 1. Here,UpperLimitandLowerLimitare the corresponding properties defined in the specification object of the input channel."rescale-symmetric"— Normalize the input by rescaling it to the interval between –1 and 1. The normalized input Y is 2(U–LowerLimit)./(UpperLimit–LowerLimit) – 1, where U is the nonnormalized input. Note that nonnormalized input values lower thanLowerLimitresult in normalized values lower than –1. Similarly, nonnormalized input values higher thanUpperLimitresult in normalized values higher than 1. Here,UpperLimitandLowerLimitare the corresponding properties defined in the specification object of the input channel.
Note
When you specify the Normalization property of
rlAgentInitializationOptions, normalization is applied only to
the approximator input channels corresponding to rlNumericSpec specification objects in which both the
UpperLimit and LowerLimit properties
are defined. After you create the agent, you can use setNormalizer to assign normalizers that use any normalization
method. For more information on normalizer objects, see rlNormalizer.
Example: "rescale-symmetric"
Computation device used to perform operations such as gradient computation, parameter
update and prediction during training and simulation, specified as either
"cpu" or "gpu".
The "gpu" option requires both Parallel Computing Toolbox™ software and a CUDA® enabled NVIDIA® GPU. For more information on supported GPUs see GPU Computing Requirements (Parallel Computing Toolbox).
You can use gpuDevice (Parallel Computing Toolbox) to query or select a local GPU device to be
used with MATLAB.
Note
Training or simulating an agent on a GPU involves device-specific numerical round-off errors. Because of these errors, you can get different results on a GPU and on a CPU for the same operation.
To speed up training by using parallel processing over multiple cores, you do not need
to use this argument. Instead, when training your agent, use an rlTrainingOptions object in which the UseParallel
option is set to true. For more information about training using
multicore processors and GPUs for training, see Train Agents Using Parallel Computing and GPUs.
Example: "gpu"
Learnable parameters of the approximator object, specified as a cell array of
dlarray objects. This property contains the learnable parameters of
the approximation model used by the approximator object.
Example: {dlarray(rand(256,4)),dlarray(rand(256,1))}
State of the approximator object, specified as a cell array of
dlarray objects. For dlnetwork-based models, this
property contains the Value column of the
State property table of the dlnetwork model.
The elements of the cell array are the state of the recurrent neural network used in the
approximator (if any), as well as the state for the batch normalization layer (if
used).
For model types that are not based on a dlnetwork object, this
property is an empty cell array, since these model types do not support states.
Example: {dlarray(rand(256,1)),dlarray(rand(256,1))}
Object Functions
rlDQNAgent | Deep Q-network (DQN) reinforcement learning agent |
rlQAgent | Q-learning reinforcement learning agent |
rlSARSAAgent | SARSA reinforcement learning agent |
getValue | Obtain estimated value from a critic given environment observations and actions |
getMaxQValue | Obtain maximum estimated value over all possible actions from a Q-value function critic with discrete action space, given environment observations |
evaluate | Evaluate function approximator object given observation (or observation-action) input data |
getLearnableParameters | Obtain learnable parameter values from agent, function approximator, or policy object |
setLearnableParameters | Set learnable parameter values of agent, function approximator, or policy object |
setModel | Set approximation model in function approximator object |
getModel | Get approximation model from function approximator object |
Examples
Create an observation specification object (or alternatively use getObservationInfo to extract the specification object from an environment). For this example, define the observation space as a continuous four-dimensional space, so that there is a single observation channel that carries a column vector containing four doubles.
obsInfo = rlNumericSpec([4 1]);
Create a discrete (finite set) action specification object (or alternatively use getActionInfo to extract the specification object from an environment with a discrete action space). For this example, define the action space as a finite set consisting of three possible actions (labeled 7, 5, and 3).
actInfo = rlFiniteSetSpec([7 5 3]);
A discrete vector Q-value function takes only the observation as input and returns as output a single vector with as many elements as the number of possible discrete actions. The value of each output element represents the expected discounted cumulative long-term reward for taking the action corresponding to the element number, from the state corresponding to the current observation, and following the policy afterwards.
To model the parametrized vector Q-value function within the critic, use a neural network with one input layer (receiving the content of the observation channel, as specified by obsInfo) and one output layer (returning the vector of values for all the possible actions, as specified by actInfo).
Define the network as an array of layer objects, and get the dimension of the observation space and the number of possible actions from the environment specification objects.
net = [
featureInputLayer(obsInfo.Dimension(1))
fullyConnectedLayer(16)
reluLayer
fullyConnectedLayer(16)
reluLayer
fullyConnectedLayer(numel(actInfo.Elements))
];Convert the network to a dlnetwork object, and display the number of weights.
net = dlnetwork(net); summary(net)
Initialized: true
Number of learnables: 403
Inputs:
1 'input' 4 features
Create the critic using the network, as well as the observation and action specification objects.
critic = rlVectorQValueFunction(net,obsInfo,actInfo)
critic =
rlVectorQValueFunction with properties:
ObservationInfo: [1×1 rl.util.rlNumericSpec]
ActionInfo: [1×1 rl.util.rlFiniteSetSpec]
Normalization: "none"
UseDevice: "cpu"
Learnables: {6×1 cell}
State: {0×1 cell}
To check your critic, use getValue to return the values of the discrete actions depending on a random observation, using the current network weights. There is one value for each of the three possible actions.
v = getValue(critic,{rand(obsInfo.Dimension)})v = 3×1 single column vector
0.0761
-0.5906
0.2072
You can now use the critic to create an agent for the environment described by the given specification objects. Examples of agents that can use a discrete vector Q-value function critic, are rlQAgent, rlDQNAgent, rlSARSAAgent and discrete rlSACAgent.
For more information on creating approximator objects such as actors and critics, see Create Policies and Value Functions.
Create an observation specification object (or alternatively use getObservationInfo to extract the specification object from an environment). For this example, define the observation space as a continuous four-dimensional space, so that there is a single observation channel that carries a column vector containing four doubles.
obsInfo = rlNumericSpec([4 1]);
Create a hybrid action specification object (or alternatively use getActionInfo to extract the specification object from an environment with a hybrid action space). For this example, define the action space as having the discrete channel carrying a scalar that can take three values (labeled -1, 0, and 1), and the continuous channel carrying a vector in which each of the three elements can vary between -10 and 10. For an hybrid action space, the discrete channel must always be the first one, and the continuous channel must be the second one.
actInfo = [
rlFiniteSetSpec([-1 0 1])
rlNumericSpec([3 1], ...
UpperLimit= 10*ones(3,1), ...
LowerLimit=-10*ones(3,1) )
];An hybrid vector Q-value function takes the observations and the continuous action as inputs and returns as output a single vector with as many elements as the number of possible discrete actions. The value of each output element represents the expected discounted cumulative long-term reward when an agent executes the discrete action corresponding to the specific output number as well as the continuous action given in input, starting from the state corresponding to the observation (also given in input), and follows the given policy afterwards.
To model the parametrized vector Q-value function within the critic, use a neural network with two input layers (receiving the content of the observation and continuous action channels, as specified by obsInfo and the second element of actInfo), and one output layer (returning the vector of values for the possible discrete actions, as specified by the first element of actInfo).
Define each network path as an array of layer objects, and get the dimension of the observation space and the number of possible actions from the environment specification objects.
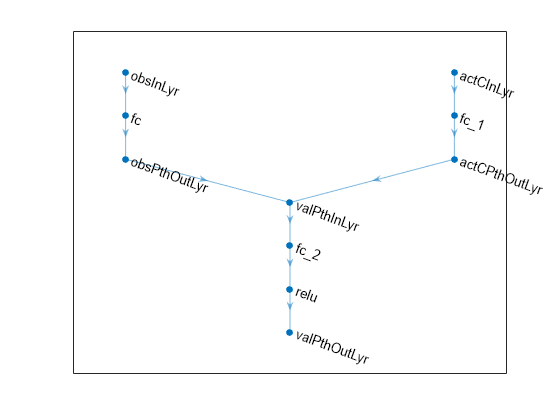
Create the observation input path.
obsPath = [
featureInputLayer( ...
prod(obsInfo.Dimension), ...
Name="obsInLyr")
fullyConnectedLayer(prod(obsInfo.Dimension))
reluLayer(Name="obsPthOutLyr")
];
Create the continuous action input path.
actCPath = [
featureInputLayer(prod(actInfo(2).Dimension), ...
Name="actCInLyr")
fullyConnectedLayer( ...
prod(actInfo(2).Dimension))
reluLayer(Name="actCPthOutLyr")
];Create common output path. Concatenate inputs along the first available dimension.
valuesPath = [
concatenationLayer(1,2,Name="valPthInLyr")
fullyConnectedLayer(numel(actInfo(1).Elements))
reluLayer
fullyConnectedLayer( ...
numel(actInfo(1).Elements), ...
Name="valPthOutLyr")
];Assemble dlnetwork object.
net = dlnetwork; net = addLayers(net,obsPath); net = addLayers(net,actCPath); net = addLayers(net,valuesPath);
Connect layers.
net = connectLayers(net,"obsPthOutLyr","valPthInLyr/in1"); net = connectLayers(net,"actCPthOutLyr","valPthInLyr/in2");
Plot network.
plot(net)
Initialize network.
net = initialize(net);
Display the number of learnable parameters.
summary(net)
Initialized: true
Number of learnables: 68
Inputs:
1 'obsInLyr' 4 features
2 'actCInLyr' 3 features
Create the critic using the network, as well as the observation and action specification objects. When you use this syntax, the network input layers are automatically associated with the environment observation channels according to the dimensions specified in obsInfo.
critic = rlVectorQValueFunction(net,obsInfo,actInfo)
critic =
rlVectorQValueFunction with properties:
ObservationInfo: [1×1 rl.util.rlNumericSpec]
ActionInfo: [2×1 rl.util.RLDataSpec]
Normalization: ["none" "none"]
UseDevice: "cpu"
Learnables: {8×1 cell}
State: {0×1 cell}
To check your critic, use getValue to return the values the discrete actions depending on a random observation and a random continuous action, using the current network weights. There is one value for each of the three possible actions.
v = getValue(critic, ...
{rand(obsInfo.Dimension),rand(actInfo(2).Dimension)})v = 3×1 single column vector
0.5603
-0.4927
0.3953
You can now use the critic to create an hybrid rlSACAgent.
For more information on creating approximator objects such as actors and critics, see Create Policies and Value Functions.
Create an observation specification object (or alternatively use getObservationInfo to extract the specification object from an environment). For this example, define the observation space as an hybrid (that is mixed discrete-continuous) space with the discrete channel carrying a scalar that can be either 0 or 1, and the second one being a vector over a continuous two-dimensional space.
obsInfo = [
rlFiniteSetSpec([0 1])
rlNumericSpec([2 1])
];Create a specification object for an hybrid action space (or alternatively use getActionInfo to extract the specification object from an environment with a hybrid action space). For this example, define the action space as an hybrid space with the discrete channel carrying a scalar that can only be -1, 0, or 1, and with the continuous channel carrying a two-element vector. Note that when defining hybrid action spaces, you must define the discrete action channel as the first one and the continuous action channel as the second one.
actInfo = [
rlFiniteSetSpec([-1 0 1])
rlNumericSpec([2 1])
];A hybrid vector Q-value function takes the observations and the continuous action as inputs and returns as output a single vector with as many elements as the number of possible discrete actions. The value of each output element represents the expected discounted cumulative long-term reward for taking the discrete action corresponding to the element number and the continuous action given as input, from the state corresponding to the current observations, and following the policy afterwards.
To model the parametrized vector Q-value function within the critic, use a neural network with three input layers and one output layer.
The input layers receive the content of the two observation channels, as specified by
obsInfoas well as the content of the continuous action channel, as specified by the second element ofactInfo. Therefore each input layer must have the same dimensions as the corresponding observation channel and an extra input layer must have the same dimensions of the continuous action channel, as specified by the second element ofactInfo.Each element of the output layer returns the value of the corresponding action. Therefore the output layer must have as many elements as the number of possible discrete actions, as specified by the first element of
actInfo.
Define each network path as an array of layer objects, and get the dimension of the observation space and the number of possible actions from the environment specification objects. Name the network inputs obs1InLyr , obs2InLyr and actCInLyr (so you can later explicitly associate it with the observation input channel).
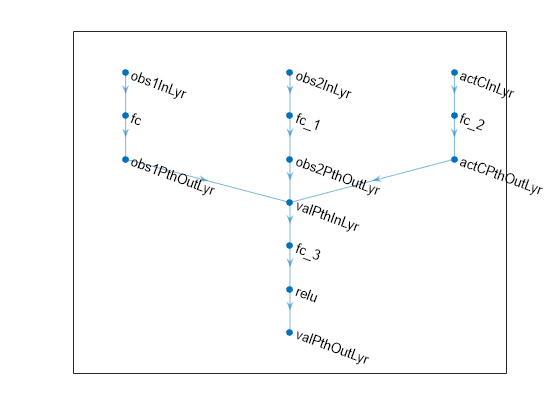
Create the first observation input path.
obs1Path = [
featureInputLayer( ...
prod(obsInfo(1).Dimension), ...
Name="obs1InLyr")
fullyConnectedLayer( ...
prod(obsInfo(1).Dimension))
reluLayer(Name="obs1PthOutLyr")
];Create the second observation input path.
obs2Path = [
featureInputLayer( ...
prod(obsInfo(2).Dimension), ...
Name="obs2InLyr")
fullyConnectedLayer( ...
prod(obsInfo(2).Dimension))
reluLayer(Name="obs2PthOutLyr")
];Create the continuous action input path.
actCPath = [
featureInputLayer( ...
prod(actInfo(2).Dimension), ...
Name="actCInLyr")
fullyConnectedLayer( ...
prod(actInfo(2).Dimension))
reluLayer(Name="actCPthOutLyr")
];Create common output path. Concatenate inputs along the first available dimension.
valuePath = [
concatenationLayer(1,3,Name="valPthInLyr")
fullyConnectedLayer(numel(actInfo(1).Elements))
reluLayer
fullyConnectedLayer( ...
numel(actInfo(1).Elements), ...
Name="valPthOutLyr")
];Assemble dlnetwork object.
net = dlnetwork; net = addLayers(net,obs1Path); net = addLayers(net,obs2Path); net = addLayers(net,actCPath); net = addLayers(net,valuePath);
Connect layers.
net = connectLayers(net,"obs1PthOutLyr","valPthInLyr/in1"); net = connectLayers(net,"obs2PthOutLyr","valPthInLyr/in2"); net = connectLayers(net,"actCPthOutLyr","valPthInLyr/in3");
Plot network.
plot(net)
Initialize network.
net = initialize(net);
Display the number of learnable parameters.
summary(net)
Initialized: true
Number of learnables: 44
Inputs:
1 'obs1InLyr' 1 features
2 'obs2InLyr' 2 features
3 'actCInLyr' 2 features
Create the critic using the network, the observations specification object, and the names of the network input layers. In this case, attempting to create a critic without using layer names will result in an error, because the dimension of the action channel is the same as the one of the continuous action channel, so the software is unable to unequivocally associate network layers with environment channels.
The specified network input layer, obsInLyr, is associated with the environment observation, and therefore must have the same data type and dimension as the observation channel specified in obsInfo.
critic = rlVectorQValueFunction(net,obsInfo,actInfo, ... ObservationInputNames={"obs1InLyr","obs2InLyr"}, ... ContinuousActionInputName="actCInLyr")
critic =
rlVectorQValueFunction with properties:
ObservationInfo: [2×1 rl.util.RLDataSpec]
ActionInfo: [2×1 rl.util.RLDataSpec]
Normalization: ["none" "none" "none"]
UseDevice: "cpu"
Learnables: {10×1 cell}
State: {0×1 cell}
To check your critic, use getValue to return the values the discrete actions depending on a random observation and a random continuous action, using the current network weights. There is one value for each of the three possible actions.
v = getValue(critic,{ ...
rand(obsInfo(1).Dimension), ...
rand(obsInfo(2).Dimension), ...
rand(actInfo(2).Dimension) })v = 3×1 single column vector
0.5075
-0.2680
0.0327
Calculate the values of the discrete actions for a batch of five independent observations and continuous actions.
v = getValue(critic,{ ...
rand([obsInfo(1).Dimension 5]), ...
rand([obsInfo(2).Dimension 5]), ...
rand([actInfo(2).Dimension 5]) })v = 3×5 single matrix
1.1344 0.4129 0.9857 0.7525 1.1961
-0.4883 -0.8504 -0.8007 -0.9811 -0.8754
0.1460 -0.7302 -0.1208 -0.4614 -0.0832
You can now use the critic to create an hybrid rlSACAgent.
For more information on creating approximator objects such as actors and critics, see Create Policies and Value Functions.
Create an observation specification object (or alternatively use getObservationInfo to extract the specification object from an environment). For this example, define the observation space as consisting of two channels, the first carrying a two-by-two continuous matrix and the second carrying scalar that can assume only two values, 0 and 1.
obsInfo = [
rlNumericSpec([2 2])
rlFiniteSetSpec([0 1])
];Create a hybrid action specification object (or alternatively use getActionInfo to extract the specification object from an environment with a hybrid action space). For this example, define a hybrid action space in which the discrete part is a vector that can have three possible values: [1 2], [3 4], and [5 6], while the continuous part is a two-dimensional continuous vector in which each element can very between -5 and 5.
actInfo = [
rlFiniteSetSpec({[1 2],[3 4],[5 6]})
rlNumericSpec([2 1], ...
UpperLimit= 5*ones(2,1), ...
LowerLimit=-5*ones(2,1) )
]; An hybrid vector Q-value function takes observations and the continuous action as inputs and returns as output a single vector with as many elements as the number of possible discrete actions. The value of each element of the output vector represents the expected discounted cumulative long-term reward when an agent executes the discrete action corresponding to the specific output number as well as the continuous action given in input, starting from the state corresponding to the observation (also given in input), and follows the given policy afterwards.
To model the parametrized vector Q-value function within the critic, use a custom basis function with three inputs and one output.
The first two inputs receive the content of the environment observation channels, as specified by
obsInfo(for this example, a matrix and a scalar, respectively).The third input receives the content of the continuous action channel, as specified by the second element of
actInfo, (for this example, a vector).The output is a vector with four elements (you can have as many elements as needed by your application).
Create a function that returns a vector of four elements, given the observations and the continuous action as inputs.
Here, the third dimension is the batch dimension. For each element of the batch dimension, the output of the basis function is a vector with four elements. Each output element can be any combination of the three inputs, depending on your application.
myBasisFcn = @(obsA,obsB,actC) [
obsA(1,1,:)+obsB(1,1,:).^2-actC(1,1,:);
obsA(2,1,:)-obsB(1,1,:).^2-actC(2,1,:);
obsA(1,2,:).^2+obsB(1,1,:)+actC(1,1,:);
obsA(2,2,:).^2-obsB(1,1,:)+actC(2,1,:);
];For each element of the batch, the output of the critic is the vector c = W'*myBasisFcn(obsA,obsB,actC), where W is a weight matrix which must have as many rows as the length of the basis function output and as many columns as the number of possible discrete actions, as specified by the first element of actInfo.
Each element of c represents the expected cumulative long term reward when an agent executes the discrete action corresponding to number of the element in c, as well as the continuous action given in input, starting from the state corresponding to the observations (also given in input), and follows the given policy afterwards.
The elements of W are the learnable parameters.
Define an initial parameter matrix.
W0 = rand(4,3);
Create the critic. The first argument is a two-element cell containing both the handle to the custom function and the initial parameter matrix. The second and third arguments are, respectively, the observation and action specification objects.
critic = rlVectorQValueFunction({myBasisFcn,W0},obsInfo,actInfo)critic =
rlVectorQValueFunction with properties:
ObservationInfo: [2×1 rl.util.RLDataSpec]
ActionInfo: [2×1 rl.util.RLDataSpec]
Normalization: ["none" "none" "none"]
UseDevice: "cpu"
Learnables: {[3×4 dlarray]}
State: {}
To check your critic, use getValue to return the values of a random observation, using the current parameter matrix. The function returns one value for each of the three possible actions.
v = getValue(critic,{rand(2,2),0,rand(2,1)})v = 3×1
1.3972
1.0399
1.5082
Note that the critic does not enforce the set constraint for the discrete set elements.
v = getValue(critic,{rand(2,2),-1,rand(2,1)})v = 3×1
2.2854
1.8893
2.5565
Obtain values for a random batch of 10 observations.
v = getValue(critic,{ ...
rand([obsInfo(1).Dimension 10]), ...
rand([obsInfo(2).Dimension 10]) ...
rand([actInfo(2).Dimension 10]) ...
});Display the values corresponding to the seventh element of the observation batch.
v(:,7)
ans = 3×1
0.8710
0.7387
0.9314
You can now use the critic to create an agent for the environment described by the given specification objects.
You can now use the critic to create an hybrid rlSACAgent.
For more information on creating approximator objects such as actors and critics, see Create Policies and Value Functions.
Create an environment and obtain observation and action specification objects.
env = rlPredefinedEnv("CartPole-Discrete");
obsInfo = getObservationInfo(env);
actInfo = getActionInfo(env);A discrete vector Q-value function takes only the observation as input and returns as output a single vector with as many elements as the number of possible actions. The value of each output element represents the expected discounted cumulative long-term reward for taking the action from the state corresponding to the current observation, and following the policy afterwards.
To model the parametrized vector Q-value function within the critic, use a recurrent neural network with one input layer (receiving the content of the observation channel, as specified by obsInfo) and one output layer (returning the vector of values for all the possible actions, as specified by actInfo).
Define the network as an array of layer objects, and get the dimension of the observation space and the number of possible actions from the environment specification objects. To create a recurrent network, use a sequenceInputLayer as the input layer (with size equal to the number of dimensions of the observation channel) and include at least one lstmLayer.
net = [
sequenceInputLayer(obsInfo.Dimension(1))
fullyConnectedLayer(50)
reluLayer
lstmLayer(20)
fullyConnectedLayer(20)
reluLayer
fullyConnectedLayer(numel(actInfo.Elements))
];Convert the network to a dlnetwork object, and display the number of weights.
net = dlnetwork(net); summary(net)
Initialized: true
Number of learnables: 6.3k
Inputs:
1 'sequenceinput' Sequence input with 4 dimensions
Create the critic using the network, as well as the observation and action specification objects.
critic = rlVectorQValueFunction(net, ...
obsInfo,actInfo);To check your critic, use getValue to return the value of a random observation and action, using the current network weights.
v = getValue(critic,{rand(obsInfo.Dimension)})v = 2×1 single column vector
0.0136
0.0067
You can use dot notation to extract and set the current state of the recurrent neural network in the critic.
critic.State
ans=2×1 cell array
{20×1 dlarray}
{20×1 dlarray}
critic.State = {
-0.1*dlarray(rand(20,1))
0.1*dlarray(rand(20,1))
};To evaluate the critic using sequential observations, use the sequence length (time) dimension. For example, obtain actions for 5 independent sequences each one consisting of 9 sequential observations.
[value,state] = getValue(critic, ...
{rand([obsInfo.Dimension 5 9])});Display the value corresponding to the seventh element of the observation sequence in the fourth sequence.
value(1,4,7)
ans = single
0.0382
Display the updated state of the recurrent neural network.
state
state=2×1 cell array
{20×5 single}
{20×5 single}
You can now use the critic to create an agent for the environment described by the given specification objects. Examples of agents that can use a vector Q-value function critic, are rlQAgent, rlDQNAgent, rlSARSAAgent, and discrete action space rlSACAgent.
For more information on creating approximator objects such as actors and critics, see Create Policies and Value Functions.
Version History
Introduced in R2022a
See Also
Functions
Objects
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Web サイトの選択
Web サイトを選択すると、翻訳されたコンテンツにアクセスし、地域のイベントやサービスを確認できます。現在の位置情報に基づき、次のサイトの選択を推奨します:
また、以下のリストから Web サイトを選択することもできます。
最適なサイトパフォーマンスの取得方法
中国のサイト (中国語または英語) を選択することで、最適なサイトパフォーマンスが得られます。その他の国の MathWorks のサイトは、お客様の地域からのアクセスが最適化されていません。
南北アメリカ
- América Latina (Español)
- Canada (English)
- United States (English)
ヨーロッパ
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)