残差分析を使用した遠心ポンプの故障診断

この例では、ポンプ システムで発生するさまざまなタイプの故障を検出して診断するモデル パリティ方程式に基づく方法を説明します。ここでは定常状態実験を使用した遠心ポンプの故障診断で提示されている手法を、ポンプの動作が複数の動作状態にわたる状況に拡張します。

ここでは Rolf Isermann 著の書籍『Fault Diagnosis Applications』で紹介されている遠心ポンプ解析を使用します [1]。System Identification Toolbox™、Statistics and Machine Learning Toolbox™、Control System Toolbox™、および Simulink® の機能を使用しますが、Predictive Maintenance Toolbox™ は必要ありません。

複数速度のポンプ運転 - 残差分析による診断

定常状態の揚程とトルクの方程式では、速度が急激に変化したり速度範囲がさらに広くなる状態でポンプを運転した場合、正確な結果を得ることができません。摩擦やその他の損失の影響が増し、モデルのパラメーターが速度に依存するようになる可能性があります。そのような場合に広く応用できる方法として、動作のブラック ボックス モデルを作成することができます。そうしたモデルのパラメーターは、物理的に有意である必要はありません。このモデルは既知の動作のシミュレーションのためのデバイスとして使用されます。モデルの出力を対応する測定信号から差し引いて "残差" を計算します。平均、分散およびべき乗などの残差のプロパティは、通常動作と故障動作を区別するために使用されます。

静的な揚程の方程式および動的なポンプ-配管の方程式を使用して、図に示されている 4 つの残差を計算することができます。

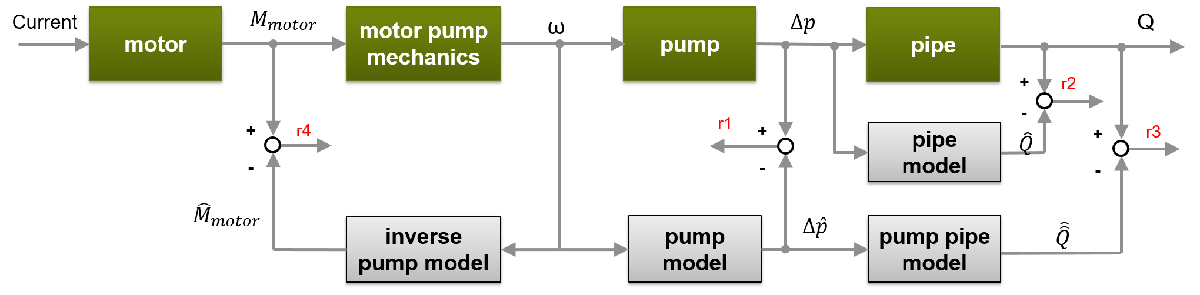
このモデルには次のコンポーネントがあります。

• 静的なポンプ モデル: $$\Delta \underset{}{\overset{ˆ}{p}}(t)={\theta }_1{\omega }^2(t)+{\theta }_2\omega (t)$$

• 動的な配管モデル: $$\underset{}{\overset{ˆ}{Q}}(t)={\theta }_3+{\theta }_4\sqrt{\Delta p(t)}+{\theta }_5\underset{}{\overset{ˆ}{Q}}(t-1)$$

• 動的なポンプ-配管モデル: $$\underset{}{\overset{ˆ}{\underset{}{\overset{ˆ}{Q}}}}(t)={\theta }_3+{\theta }_4\sqrt{\underset{}{\overset{ˆ}{\Delta p(t)}}}+{\theta }_5\underset{}{\overset{ˆ}{\underset{}{\overset{ˆ}{Q}}}}(t-1)$$

• 動的な逆ポンプ モデル: $${\underset{}{\overset{ˆ}{M}}}_{motor}(t)={\theta }_6+{\theta }_7\omega (t)+{\theta }_8\omega (t-1)+{\theta }_9{\omega }^2(t)+{\theta }_{10}{\underset{}{\overset{ˆ}{M}}}_{motor}(t-1)$$

モデル パラメーター $${\theta }_1,...,{\theta }_{10}$$ はポンプ回転数への依存を示しています。この例では、パラメーターの区分的線形近似を計算します。動作領域を 3 つの領域に分割します。

1. $$\omega \le 900RPM$$

2. $$900<\omega \le 1500RPM$$

3. $$\omega >1500RPM$$

健全なポンプが、基準速度範囲 0 ～ 3000 RPM において、閉ループのコントローラーをもつ閉ループで実行されています。基準入力は修正 PRBS 信号です。モーター トルク、ポンプ トルク、速度および圧力の測定値は 10 Hz のサンプリング周波数で収集しました。測定した信号を読み込み、基準と実際のポンプ速度をプロットします (これらは最大 20 MB の大規模なデータセットで、MathWorks® サポート ファイル サイトからダウンロードします)。

url = 'https://www.mathworks.com/supportfiles/predmaint/fault-diagnosis-of-centrifugal-pumps-using-residual-analysis/DynamicOperationData.mat';
websave('DynamicOperationData.mat',url);
load DynamicOperationData
figure
plot(t, RefSpeed, t, w)
xlabel('Time (s)')
ylabel('Pump Speed (RPM)')
legend('Reference','Actual')

ポンプ速度の範囲に基づいて動作範囲を定義します。

I1 = w<=900;            % first operating regime
I2 = w>900 & w<=1500;   % second operating regime
I3 = w>1500;            % third operating regime

モデルの同定

A. 静的なポンプ モデルの同定

ポンプ回転数 $\omega \left(\mathit{t}\right)$ と圧力差 $\Delta \mathit{p}\left(\mathit{t}\right)$ の測定値を入出力データとして使用して、静的なポンプ方程式のパラメーター ${\theta }_1$ および ${\theta }_2$ を推定します。この推定を実行する補助関数 staticPumpEst を参照してください。

th1 = zeros(3,1);  
th2 = zeros(3,1); 
dpest = nan(size(dp));  % estimated pressure difference
[th1(1), th2(1), dpest(I1)] = staticPumpEst(w, dp, I1);  % Theta1, Theta2 estimates for regime 1
[th1(2), th2(2), dpest(I2)] = staticPumpEst(w, dp, I2);  % Theta1, Theta2 estimates for regime 2
[th1(3), th2(3), dpest(I3)] = staticPumpEst(w, dp, I3);  % Theta1, Theta2 estimates for regime 3
plot(t, dp, t, dpest) % compare measured and predicted pressure differential
xlabel('Time (s)')
ylabel('\Delta P')
legend('Measured','Estimated','Location','best')
title('Static Pump Model Validation')

B. 動的な配管モデルの同定

流量 $\mathit{Q}\left(\mathit{t}\right)$ と圧力差 $\Delta \mathit{p}\left(\mathit{t}\right)$ の測定値を入出力データとして使用して、配管吐出流の方程式 $$\underset{}{\overset{ˆ}{Q}}(t)={\theta }_3+{\theta }_4\sqrt{\Delta p(t)}+{\theta }_5\underset{}{\overset{ˆ}{Q}}(t-1)$$ のパラメーター ${\theta }_3$、${\theta }_4$、および ${\theta }_5$ を推定します。この推定を実行する補助関数 dynamicPipeEst を参照してください。

th3 = zeros(3,1);  
th4 = zeros(3,1); 
th5 = zeros(3,1);
[th3(1), th4(1), th5(1)] = dynamicPipeEst(dp, Q, I1); % Theta3, Theta4, Theta5 estimates for regime 1
[th3(2), th4(2), th5(2)] = dynamicPipeEst(dp, Q, I2); % Theta3, Theta4, Theta5 estimates for regime 2
[th3(3), th4(3), th5(3)] = dynamicPipeEst(dp, Q, I3); % Theta3, Theta4, Theta5 estimates for regime 3

静的なポンプ モデルの場合と異なり、動的な配管モデルは流量値への動的な依存を示しています。速度状態を変化させてモデルをシミュレートするため、Control System Toolbox の "LPV System" ブロックを使用して Simulink で区分的線形モデルが作成されます。Simulink モデル LPV_pump_pipe と、このシミュレーションを実行する補助関数 simulatePumpPipeModel を参照してください。

% Check Control System Toolbox availability
ControlsToolboxAvailable = ~isempty(ver('control')) && license('test', 'Control_Toolbox');
if ControlsToolboxAvailable
    % Simulate the dynamic pipe model. Use measured value of pressure as input
    Ts = t(2)-t(1);
    Switch = ones(size(w));
    Switch(I2) = 2;
    Switch(I3) = 3;
    UseEstimatedP = 0;
    Qest_pipe = simulatePumpPipeModel(Ts,th3,th4,th5);
    plot(t,Q,t,Qest_pipe) % compare measured and predicted flow rates
else
    % Load pre-saved simulation results from the piecewise linear Simulink model
    load DynamicOperationData Qest_pipe
    Ts = t(2)-t(1);
    plot(t,Q,t,Qest_pipe)
end
xlabel('Time (s)')
ylabel('Flow rate (Q), m^3/s')
legend('Measured','Estimated','Location','best')
title('Dynamic Pipe Model Validation')

C. 動的なポンプ配管モデルの同定

動的なポンプ-配管モデルは、上記で特定したものと同じパラメーター ($${\theta }_3,{\theta }_4,{\theta }_5$$) を使用しますが、モデルのシミュレーションでは測定した値ではなく推定した圧力差を使用する必要があります。したがって、新しい同定の必要はありません。$${\theta }_3,{\theta }_4,{\theta }_5$$ の推定値によって、ポンプと配管のダイナミクスが適切に再現されることを確認します。

if ControlsToolboxAvailable
    UseEstimatedP = 1;
    Qest_pump_pipe = simulatePumpPipeModel(Ts,th3,th4,th5);
    plot(t,Q,t,Qest_pump_pipe) % compare measured and predicted flow rates
else
    load DynamicOperationData Qest_pump_pipe 
    plot(t,Q,t,Qest_pump_pipe)
end

xlabel('Time (s)')
ylabel('Flow rate Q (m^3/s)')
legend('Measured','Estimated','location','best')
title('Dynamic Pump-Pipe Model Validation')

適合は、測定した圧力値を使って取得したものと事実上同一です。

D. 動的な逆ポンプ モデルの同定

測定したトルク値を前のトルクと速度の測定値に回帰させることにより、パラメーター $${\theta }_6,...,{\theta }_{10}$$ を同様の方法で特定できます。しかし、結果の区分的線形モデルの完全な複数速度シミュレーションでは、データへの適切な当てはめが得られません。そのため、異なるブラック ボックスのモデル化の方法を試します。これにはデータに当てはめる有理リグレッサーをもつ非線形 ARX モデルの同定が含まれます。

% Use first 300 samples out of 550 for identification
N = 350;
sys3 = identifyNonlinearARXModel(Mmot,w,Q,Ts,N)

sys3 =

Nonlinear ARX model with 1 output and 2 inputs
  Inputs: u1, u2
  Outputs: y1

Regressors:
  1. Linear regressors in variables y1, u1, u2
  2. Custom regressor: u1(t-2)^2
  3. Custom regressor: u1(t)*u2(t-2)
  4. Custom regressor: u2(t)^2
  List of all regressors

Output function: Linear with offset
Sample time: 0.1 seconds

Status:                                          
Estimated using NLARX on time domain data.       
Fit to estimation data: 49.27% (simulation focus)
FPE: 1798, MSE: 3383                             

Model Properties

Mmot_est = sim(sys3,[w Q]);
plot(t,Mmot,t,Mmot_est) % compare measured and predicted motor torque
xlabel('Time (s)')
ylabel('Motor Torque (Nm)')
legend('Measured','Estimated','location','best')
title('Inverse pump model validation')

残差の生成

モデルの "残差" を、測定信号と、モデルで生成された対応する出力との差として定義します。4 つのモデル コンポーネントに対応する 4 つの残差を計算します。

r1 = dp - dpest;
r2 = Q - Qest_pipe;
r3 = Q - Qest_pump_pipe;

逆ポンプ モデル残差の計算には、元の残差に大きな分散が見られるため、移動平均フィルターを使用してモデル出力に平滑化操作を適用します。

r4 = Mmot - movmean(Mmot_est,[1 5]);

学習残差のビュー:

figure
subplot(221)
plot(t,r1)
ylabel('Static pump - r1')
subplot(222)
plot(t,r2)
ylabel('Dynamic pipe - r2')
subplot(223)
plot(t,r3)
ylabel('Dynamic pump-pipe - r3')
xlabel('Time (s)')
subplot(224)
plot(t,r4)
ylabel('Dynamic inverse pump - r4')
xlabel('Time (s)')

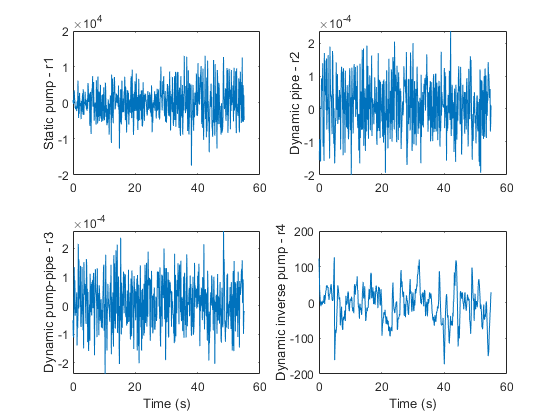
残差特徴の抽出

残差は、故障特定のための適切な特徴を抽出する信号です。利用できるパラメーター情報がないため、信号の最大振幅や分散などの信号プロパティのみから求められる特徴を考慮します。

PRBS 入力実現を使用したポンプ-配管システムに対する 20 の実験セットを考えます。次の各モードについて実験セットを繰り返します。

1. 健全なポンプ

2. 故障 1: クリアランスの隙間にある摩損

3. 故障 2: インペラー出口にある少量の堆積物

4. 故障 3: インペラー入口にある堆積物

5. 故障 4: インペラー出口にある摩耗

6. 故障 5: ブレード折損

7. 故障 6: キャビテーション

8. 故障 7: 速度センサー バイアス

9. 故障 8: 流量計バイアス

10. 故障 9: 圧力センサー バイアス

実験データを読み込みます。

url = 'https://www.mathworks.com/supportfiles/predmaint/fault-diagnosis-of-centrifugal-pumps-using-residual-analysis/MultiSpeedOperationData.mat';
websave('MultiSpeedOperationData.mat',url);
load MultiSpeedOperationData
% Generate operation mode labels
Labels = {'Healthy','ClearanceGapWear','ImpellerOutletDeposit',...
    'ImpellerInletDeposit','AbrasiveWear','BrokenBlade','Cavitation','SpeedSensorBias',...
    'FlowmeterBias','PressureSensorBias'};

各アンサンブルおよび各操作モードにつき残差を計算します。これには数分かかります。したがって、残差データはデータ ファイルに格納されます。以下に示すように、helperComputeEnsembleResidues を実行して残差を生成します。

% HealthyR = helperComputeEnsembleResidues(HealthyEnsemble,Ts,sys3,th1,th2,th3,th4,th5); % Healthy data residuals

% Load pre-saved data from "helperComputeEnsembleResidues" run
url = 'https://www.mathworks.com/supportfiles/predmaint/fault-diagnosis-of-centrifugal-pumps-using-residual-analysis/Residuals.mat';
websave('Residuals.mat',url);
load Residuals

モード区別の能力が最も高い残差の特徴は事前に知られていません。そのため、各残差について平均、最大振幅、分散、尖度、1 ノルムなど、候補の特徴をいくつか生成します。すべての特徴が、健全なアンサンブルにおける値の範囲を使用してスケーリングされます。

CandidateFeatures = {@mean, @(x)max(abs(x)), @kurtosis, @var, @(x)sum(abs(x))};
FeatureNames = {'Mean','Max','Kurtosis','Variance','OneNorm'};
% generate feature table from gathered residuals of each fault mode
[HealthyFeature, MinMax] = helperGenerateFeatureTable(HealthyR, CandidateFeatures, FeatureNames);
Fault1Feature  = helperGenerateFeatureTable(Fault1R,  CandidateFeatures, FeatureNames, MinMax);
Fault2Feature  = helperGenerateFeatureTable(Fault2R,  CandidateFeatures, FeatureNames, MinMax);
Fault3Feature  = helperGenerateFeatureTable(Fault3R,  CandidateFeatures, FeatureNames, MinMax);
Fault4Feature  = helperGenerateFeatureTable(Fault4R,  CandidateFeatures, FeatureNames, MinMax);
Fault5Feature  = helperGenerateFeatureTable(Fault5R,  CandidateFeatures, FeatureNames, MinMax);
Fault6Feature  = helperGenerateFeatureTable(Fault6R,  CandidateFeatures, FeatureNames, MinMax);
Fault7Feature  = helperGenerateFeatureTable(Fault7R,  CandidateFeatures, FeatureNames, MinMax);
Fault8Feature  = helperGenerateFeatureTable(Fault8R,  CandidateFeatures, FeatureNames, MinMax);
Fault9Feature  = helperGenerateFeatureTable(Fault9R,  CandidateFeatures, FeatureNames, MinMax);

各特徴テーブルには 20 の特徴 (残差信号ごとに 5 つの特徴) があります。各テーブルは、各実験から 1 つずつ、50 の観測値 (行) を含みます。

N = 50; % number of experiments in each mode
FeatureTable = [...
   [HealthyFeature(1:N,:), repmat(Labels(1),[N,1])];...
   [Fault1Feature(1:N,:),  repmat(Labels(2),[N,1])];...
   [Fault2Feature(1:N,:),  repmat(Labels(3),[N,1])];...
   [Fault3Feature(1:N,:),  repmat(Labels(4),[N,1])];...
   [Fault4Feature(1:N,:),  repmat(Labels(5),[N,1])];...
   [Fault5Feature(1:N,:),  repmat(Labels(6),[N,1])];...
   [Fault6Feature(1:N,:),  repmat(Labels(7),[N,1])];...
   [Fault7Feature(1:N,:),  repmat(Labels(8),[N,1])];...
   [Fault8Feature(1:N,:),  repmat(Labels(9),[N,1])];...
   [Fault9Feature(1:N,:),  repmat(Labels(10),[N,1])]];
FeatureTable.Properties.VariableNames{end} = 'Condition';

% Preview some samples of training data
disp(FeatureTable([2 13 37 49 61 62 73 85 102 120],:))

     Mean1       Mean2      Mean3      Mean4      Max1        Max2        Max3        Max4       Kurtosis1    Kurtosis2    Kurtosis3    Kurtosis4     Variance1    Variance2    Variance3    Variance4    OneNorm1    OneNorm2    OneNorm3    OneNorm4            Condition        
    ________    _______    _______    _______    _______    ________    ________    _________    _________    _________    _________    __________    _________    _________    _________    _________    ________    ________    ________    ________    _________________________

     0.32049     0.6358     0.6358    0.74287    0.39187     0.53219     0.53219     0.041795      0.18957    0.089492     0.089489              0     0.45647       0.6263       0.6263      0.15642      0.56001    0.63541     0.63541      0.24258    {'Healthy'              }
     0.21975    0.19422    0.19422    0.83704          0     0.12761     0.12761      0.27644      0.18243     0.19644      0.19643        0.20856    0.033063      0.16772      0.16773     0.025119     0.057182    0.19344     0.19344     0.063167    {'Healthy'              }
      0.1847    0.25136    0.25136    0.87975    0.32545     0.13929      0.1393     0.084162      0.72346    0.091488     0.091485       0.052552    0.063757      0.18371      0.18371     0.023845      0.10671    0.25065     0.25065      0.04848    {'Healthy'              }
           1          1          1          0    0.78284     0.94535     0.94535       0.9287      0.41371     0.45927      0.45926        0.75934     0.92332            1            1      0.80689      0.99783          1           1       0.9574    {'Healthy'              }
     -2.6545    0.90555    0.90555    0.86324     1.3037      0.7492      0.7492      0.97823    -0.055035     0.57019      0.57018         1.4412      1.4411      0.73128      0.73128      0.80573       3.2084    0.90542     0.90542      0.49257    {'ClearanceGapWear'     }
    -0.89435    0.43384    0.43385     1.0744    0.82197     0.30254     0.30254    -0.022325      0.21411    0.098504       0.0985      -0.010587     0.55959      0.29554      0.29554     0.066693       1.0432    0.43326     0.43326      0.13785    {'ClearanceGapWear'     }
     -1.2149    0.53579    0.53579     1.0899    0.87439     0.47339     0.47339      0.29547     0.058946    0.048138     0.048137        0.17864     0.79648      0.48658      0.48658      0.25686       1.4066     0.5353      0.5353      0.26663    {'ClearanceGapWear'     }
     -1.0949    0.44616    0.44616      1.143    0.56693     0.19719     0.19719    -0.012055     -0.10819     0.32603      0.32603     -0.0033592     0.43341      0.12857      0.12857     0.038392       1.2238    0.44574     0.44574     0.093243    {'ClearanceGapWear'     }
     -0.1844    0.16651    0.16651    0.87747    0.25597    0.080265    0.080265      0.49715       0.5019     0.29939      0.29938         0.5338    0.072397     0.058024     0.058025       0.1453      0.20263    0.16566     0.16566      0.14216    {'ImpellerOutletDeposit'}
     -3.0312     0.9786     0.9786    0.75241      1.473     0.97839     0.97839       1.0343    0.0050647      0.4917       0.4917        0.89759      1.7529       0.9568       0.9568       0.8869       3.6536    0.97859     0.97859      0.62706    {'ImpellerOutletDeposit'}

分類器の設計

A. 散布図を使用したモードの分離可能性の可視化

特徴の視覚検査によって解析を始めます。そのためには、故障 1: クリアランスの隙間にある摩損について考えます。この故障を検出するのに最も適した特徴を表示するため、'Healthy' と 'ClearanceGapWear' のラベルを使って特徴の散布図を生成します。

T = FeatureTable(:,1:20);
P = T.Variables;
R = FeatureTable.Condition;
I = strcmp(R,'Healthy') | strcmp(R,'ClearanceGapWear');
f = figure;
gplotmatrix(P(I,:),[],R(I))
f.Position(3:4) = f.Position(3:4)*1.5;

明確には見えませんが、1 列目と 17 列目の特徴で最もよく分離しています。これらの特徴をさらに詳しく解析します。

f = figure;
Names = FeatureTable.Properties.VariableNames;
J = [1 17];
fprintf('Selected features for clearance gap fault: %s\n',strjoin(Names(J),', '))

Selected features for clearance gap fault: Mean1, OneNorm1

gplotmatrix(P(I,[1 17]),[],R(I))

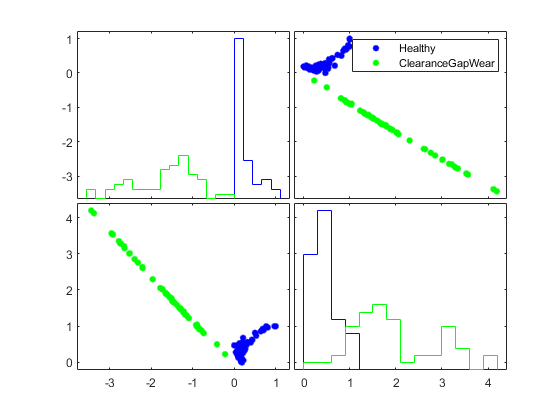
これでプロットには、特徴 Mean1 および OneNorm1 を使用して、クリアランスの隙間の故障モードから健全モードを分離できることが明確に示されます。同様の解析を各故障モードについて実行できます。すべてのケースにおいて、故障モードを区別する特徴のセットを見つけることができます。したがって、故障動作の "検出" は常に可能です。ただし、同じ特徴に影響する故障タイプが複数あるため、故障の "特定" はより困難になります。たとえば、特徴 Mean1 (r1 の平均) と特徴 OneNorm1 (r1 の 1 ノルム) は多くの故障タイプで変化が見られます。同時に、センサー バイアスなど一部の故障は、多くの特徴において故障の特定が可能であり、比較的簡単に分離できます。

3 つのセンサー バイアス故障については、散布図の手動検査からの特徴を選択します。

figure;
I = strcmp(R,'Healthy') | strcmp(R,'PressureSensorBias') | strcmp(R,'SpeedSensorBias') | strcmp(R,'FlowmeterBias');
J = [1 4 6 16 20]; % selected feature indices
fprintf('Selected features for sensors'' bias: %s\n',strjoin(Names(J),', '))

Selected features for sensors' bias: Mean1, Mean4, Max2, Variance4, OneNorm4

gplotmatrix(P(I,J),[],R(I))

選択した特徴の散布図は、4 つのモードが 1 つ以上の特徴ペアにより区別できることを示しています。故障の簡約セット (センサー バイアスのみ) に対し、特徴の簡約セットを使用して 20 メンバーのツリー バガー分類器に学習させます。

rng default % for reproducibility
Mdl = TreeBagger(20, FeatureTable(I,[J 21]), 'Condition',...
   'OOBPrediction','on',...
   'OOBPredictorImportance','on');
figure
plot(oobError(Mdl))
xlabel('Number of trees')
ylabel('Misclassification probability')

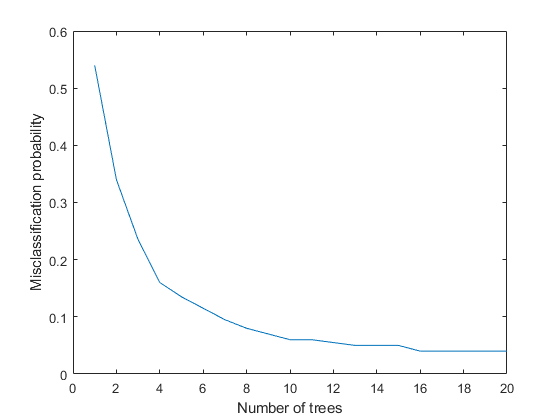
誤分類のエラーは 3% 未満です。したがって、故障の特定のサブセットを分類するため、さらに少ない数の特徴のセットを選択し、取り扱うことが可能です。

B. 分類学習器アプリを使用した複数クラス分類器

前の節では散布図の手動検査に注目し、特定の故障タイプについて特徴セットを小さくしました。この方法は手間がかかり、すべての故障タイプをカバーしない可能性があります。さらに自動化された方法ですべての故障モードに対処できる分類器を設計することは可能でしょうか。Statistics and Machine Learning Toolbox には数多くの分類器が用意されています。短時間でこれらの多くを試してその性能を比較する 1 つの方法として、分類学習器アプリを使用できます。

1. 分類学習器アプリを起動して、ワークスペースから、新しいセッションの作業データとして FeatureTable を選択します。ホールドアウト検証のためにデータの 20% (各モードの 10 のサンプル) を確保しておきます。

2. メイン タブの [モデル タイプ] セクションで、[すべて] を選択します。次に [学習] ボタンを押します。

3. 短時間で 20 の分類器の学習が行われます。これらの正確性は、履歴パネルでその名前の横に表示されます。線形 SVM 分類器の性能が最良であり、ホールド アウト サンプルでは 86% の正確性が得られます。この分類器では "ClearanceGapWear" の識別がやや難しく、40% の確率で "ImpellerOutletDeposit" として分類されます。

4. 性能のグラフィカル ビューを得るには、メイン タブの [プロット] セクションから混同行列プロットを開きます。プロットは、選択した分類器 (ここでは線形 SVM 分類器) の性能を示します。

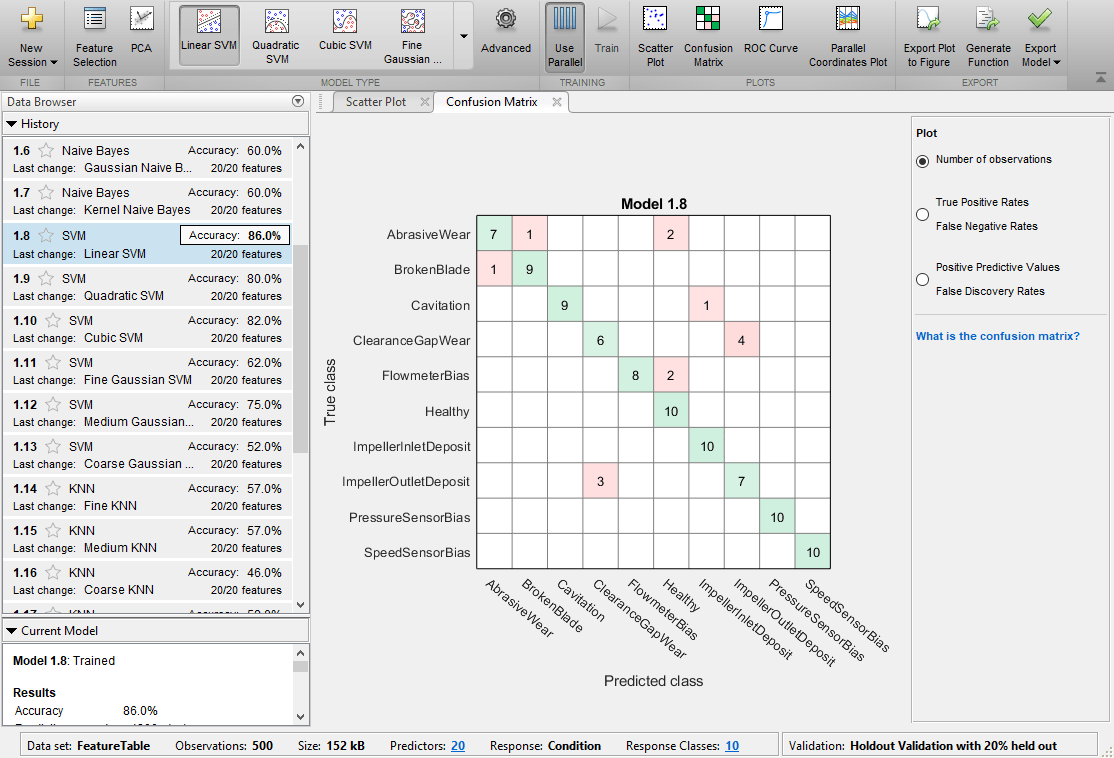
最も性能が良い分類器をワークスペースにエクスポートして、新しい測定値に対する予測に使用します。

まとめ

設計の優れた故障診断手法によって、サービスのダウンタイムとコンポーネントの交換費用を最小限に抑えることで運用コストを節約できます。この手法は、稼働するマシンのダイナミクスに関する適切な知識があると有利で、これとセンサー測定値を組み合わせて使用して、異なる種類の故障を検出し特定します。この例では、遠心ポンプの故障診断のための残差に基づく方法について説明しました。この方法は、モデル化タスクが複雑でモデル パラメーターに動作状態への依存が見られる場合に、パラメーターの推定と追跡に基づく方法の良い代替となります。

残差に基づく故障診断方法は以下の手順で行われます。

1. 物理的な考慮事項またはブラック ボックスのシステム同定手法を使用して、システムの測定可能な入力と出力の間のダイナミクスをモデル化します。

2. 測定した信号とモデルで生成された信号の差として残差を計算します。必要に応じて、故障特定可能性を改善するために残差をさらにフィルター処理します。

3. 各残差信号からピーク振幅、電力、尖度などの特徴を抽出します。

4. 異常検出と分類の手法を用いて、故障の検出と分類のための特徴を使用します。

5. すべての残差および求められた特徴が、すべての故障の影響を受けるとは限りません。特徴ヒストグラムと散布図のビューによって、特定の故障タイプを検出するにはどの特徴が適しているかが明らかになります。特徴を選択し、故障特定におけるその性能を評価するこの過程は、反復手順となる場合もあります。

参考文献

1. Isermann, Rolf, Fault-Diagnosis Applications.Model-Based Condition Monitoring:Actuators, Drives, Machinery, Plants, Sensors, and Fault-tolerant System, Edition 1, Springer-Verlag Berlin Heidelberg, 2011.

サポート関数

静的なポンプ方程式のパラメーター推定

function [x1, x2, dpest] = staticPumpEst(w, dp, I)
%staticPumpEst Static pump parameter estimation in a varying speed setting
% I: sample indices for the selected operating region.

w1 = [0; w(I)];
dp1 = [0; dp(I)];
R1 = [w1.^2 w1];
x = pinv(R1)*dp1;
x1 = x(1);  
x2 = x(2);  

dpest = R1(2:end,:)*x;
end

動的な配管のパラメーター推定

function [x3, x4, x5, Qest] = dynamicPipeEst(dp, Q, I)
%dynamicPipeEst Dynamic pipe parameter estimation in a varying speed setting
% I: sample indices for the selected operating region.

Q = Q(I);
dp = dp(I);
R1 = [0; Q(1:end-1)];
R2 = dp; R2(R2<0) = 0; R2 = sqrt(R2);
R = [ones(size(R2)), R2, R1];

% Remove out-of-regime samples
ii = find(I);
j = find(diff(ii)~=1);
R = R(2:end,:); R(j,:) = [];
y = Q(2:end); y(j) = [];
x = R\y;

x3 = x(1);
x4 = x(2);
x5 = x(3);

Qest = R*x;
end

LPV System ブロックを使用した、ポンプ-配管モデルの動的な複数操作モード シミュレーション。

function Qest = simulatePumpPipeModel(Ts,th3,th4,th5)
%simulatePumpPipeModel Piecewise linear modeling of dynamic pipe system.
% Ts: sample time
% w: Pump rotational speed
% th1, th2, th3 are estimated model parameters for the 3 regimes.
% This function requires Control System Toolbox.

ss1 = ss(th5(1),th4(1),th5(1),th4(1),Ts);
ss2 = ss(th5(2),th4(2),th5(2),th4(2),Ts);
ss3 = ss(th5(3),th4(3),th5(3),th4(3),Ts);
offset = permute([th3(1),th3(2),th3(3)]',[3 2 1]);
OP = struct('Region',[1 2 3]');
sys = cat(3,ss1,ss2,ss3);
sys.SamplingGrid = OP;

assignin('base','sys',sys)
assignin('base','offset',offset)
mdl = 'LPV_pump_pipe';
sim(mdl);
Qest = logsout.get('Qest');
Qest = Qest.Values;
Qest = Qest.Data;
end

逆ポンプ ダイナミクスの動的なモデルの特定。

function syse = identifyNonlinearARXModel(Mmot,w,Q,Ts,N)
%identifyNonlinearARXModel Identify a nonlinear ARX model for 2-input (w, Q), 1-output (Mmot) data.
% Inputs:
%  w: rotational speed
%  Q: Flow rate
%  Mmot: motor torque
%  N: number of data samples to use
% Outputs:
%  syse: Identified model
%
% This function uses NLARX estimator from System Identification Toolbox.

sys = idnlarx([2 2 1 0 1],'','CustomRegressors',{'u1(t-2)^2','u1(t)*u2(t-2)','u2(t)^2'});
data = iddata(Mmot,[w Q],Ts);
opt = nlarxOptions;
opt.Focus = 'simulation';
opt.SearchOptions.MaxIterations = 500;
syse = nlarx(data(1:N),sys,opt);
end

参考

トピック

• 故障の検出と診断のための判定モデル