定常状態実験を使用した遠心ポンプの故障診断

ライブスクリプトを開く

この例では、ポンプシステムで発生するさまざまなタイプの故障の検出と診断のためのモデルベースの方法を説明します。ここでは Rolf Isermann 著の書籍『Fault Diagnosis Applications』で紹介されている遠心ポンプ解析を使用します [1]。

ポンプの監視と故障検出

ポンプは電力、化学、鉱物・鉱業、製造、暖房、冷房、冷却などの多くの産業にとって欠かせない装置です。遠心ポンプは、回転運動エネルギーを流体流動の流体力学的エネルギーに変換することよって流体を輸送するために使用されます。回転エネルギーは通常、内燃エンジンあるいは電気モーターから得られます。流体はポンプの回転軸に沿ってあるいはその付近からインペラーに入り、インペラーで加速されて、外へ向けて放射状にディフューザーへと流入します。

ポンプにはその液圧または機械コンポーネントへの損傷が生じます。最もよく故障するコンポーネントはスライドリングシールとボールベアリングですが、駆動モーター、インペラーブレード、すべりベアリングなど、その他のコンポーネントの故障も珍しくありません。下の表に、最も一般的な故障のタイプを示します。

キャビテーション: 静圧が蒸気圧より低くなると流体中に気泡ができます。気泡が突然弾けた結果、羽根車が破損します。
気体混入: 圧力の低下により液中に気体が混入します。気体と液体の分離および水頭の低下が生じます。
空運転: 水分がないために冷却が不足してベアリングが過熱します。始動段階で重要です。
壊食: 硬い粒子やキャビテーションに起因する壁への機械的損傷。
腐食: 浸食性の流体による損傷。
ベアリングの摩耗: 疲労や金属摩擦、孔食や裂傷ができることによる機械的な損傷。
逃がし試錐孔の閉塞: アキシャルベアリングの過負荷や損傷につながります。
スライドリングシールの閉塞: 摩擦の増加と効率性の低下につながります。
分割型シールの増加: 効率性の損失につながります。
堆積物: 有機物質あるいはローター入口または出口での化学反応による堆積物のため、効率性が低下して温度が上昇します。
発振: ローターの損傷または堆積物によるローターの不均衡。ベアリング破損の原因となり得ます。

利用できるセンサー

通常、以下の信号が測定されます。

入口と出口の間の圧力差 $Δ p$
回転速度 $ω$
モータートルク $M_{mot}$ およびポンプトルク $M_{p}$
ポンプ出口での流体吐出率 (流量) $Q$
駆動モーター電流、電圧、温度 (ここでは考慮しません)
流体温度、沈殿物 (ここでは考慮しません)

ポンプと配管系統の数学的なモデル

ラジアル遠心ポンプのローターに適用されるトルク $M$ によって回転速度が $ω$ となり、半径の小さいローター入口から半径の大きいローター出口へ、ポンプ流体の運動量増加が伝えられます。オイラーのタービン方程式により、圧力差 $Δ p$ 、速度 $ω$ 、および流体吐出率 (流量) $Q$ の間の関係が求められます。

$H_{t h} = h_{1} ω^{2} - h_{2} ω Q$

ここで、 $H_{t h} = \frac{Δ p}{ρ g}$ はメートル単位で測定された理論上の (損失なしの理想的な) 揚程であり、 $h_{1}$ と $h_{2}$ は比例定数です。有限個のインペラーブレード、摩擦損失および非接線流に起因する影響損失を考慮すると、実揚程は次で与えられます。

$H = h_{n n} ω^{2} - h_{n v} ω Q - h_{v v} Q^{2}$

ここで、 $h_{nn}$ 、 $h_{n v}$ 、および $h_{vv}$ は比例定数であり、モデルパラメーターとして扱われます。対応するポンプトルクは次のとおりです。

$M_{P} = ρ g (h_{n n} ω Q - h_{n v} Q^{2} - h_{v v} \frac{Q^{3}}{ω})$

モーターとポンプの機械部分によって、次のようにトルクが適用されると速度が高まります。

$J_{P} \frac{d ω (t)}{d t} = M_{m o t} (t) - M_{P} (t) - M_{f} (t)$

ここで、 $J_{P}$ はモーターとポンプの慣性の比率、 $M_{f}$ はクーロン摩擦 $M_{f 0}$ および粘性摩擦 $M_{f 1} ω (t)$ からなる摩擦トルクで、次のように定義されます。

$M_{f} (t) = M_{f 0} s i g n ω (t) + M_{f 1} ω (t)$

このポンプは流体を低いところにある貯蔵タンクから高いところにある貯蔵タンクに送る配管系統につながれています。モーメントの釣合方程式により次が得られます。

$H (t) = a_{F} \frac{d Q (t)}{d t} + h_{r r} Q^{2} (t) + H_{s t a t i c}$

ここで、 $h_{r r}$ は管の長さが $l$ で断面積が $A$ の配管 $a_{F} = \frac{l}{g A}$ の抵抗係数、 $H_{s t a t i c}$ はポンプより上にある貯蔵タンクの高さです。モデルパラメーター $h_{n n}, h_{n v}, h_{v v}$ は、物理学から既知であるか、測定されたセンサー信号をモデルの入出力に当てはめて推定することができます。使用されるモデルのタイプは、ポンプを運転する動作状態に依存します。たとえば、ポンプを常に一定の角速度で運転する場合、ポンプ-配管システムの完全な非線形モデルは必要ではないかもしれません。

故障検出の手法

測定値から抽出された特定の特徴を調べ、それらを許容される動作の既知のしきい値と比較することによって、故障を検出できます。さまざまな故障の検出可能性と特定可能性は、実験の性質と測定値の可用性により異なります。たとえば、圧力の測定値を使用した一定速度解析では、大きな圧力変化を生じさせる故障のみを検出できます。また、故障の原因を正確に評価することはできません。しかし、圧力差、モータートルク、および流量の測定値を使用した複数速度の実験では、気体混入、空運転、大量の堆積物、モーター欠陥などに起因する数多くの故障原因を検出し特定することが可能です。

モデルベースの方法は以下の手法を使用します。

パラメーター推定: マシンの健全な (ノミナル) 動作からの測定値を使用して、モデルのパラメーターを推定し、その不確かさを定量化します。その後、テストシステムの測定値を使用してパラメーター値を再び推定し、結果の推定値をそのノミナル値と比較します。この手法がこの例の主なトピックとなっています。
残差の生成: 前と同じように健全なマシンに対してモデルを学習させます。モデルの出力をテストシステムから測定された観察値と比較し、残差信号を計算します。この信号についてその振幅、分散、およびその他のプロパティを解析し、故障を検出します。数多くの残差を設計および使用して、故障のさまざまな原因を区別できます。この手法は "残差分析を使用した遠心ポンプの故障診断" の例で説明されています。

一定速度の実験: パラメーター推定による故障解析

ポンプのキャリブレーションと監視のための一般的な方法の 1 つは、これを一定速度で運転してポンプの静揚程および流体吐出率を記録する方法です。配管系統のバルブ位置を変更することによって流体吐出体積 (GPM) を制御します。吐出率が増加すると揚程は低下します。ポンプの測定水頭特性を、製造元が提供した値と比較できます。差がある場合は故障の可能性を示しています。吐出水頭と流出率の測定値は、Simulink でのポンプ-配管システムモデルのシミュレーションにより得られたものです。

定格速度である 2900 RPM では、製造元から提供された健全なポンプの理想的な揚程特性は次のようになります。

url = 'https://www.mathworks.com/supportfiles/predmaint/fault-diagnosis-of-centrifugal-pumps-using-steady-state-experiments/PumpCharacteristicsData.mat';
websave('PumpCharacteristicsData.mat',url);
load PumpCharacteristicsData Q0 H0 M0 % manufacturer supplied data for pump's delivery head
figure
plot(Q0, H0, '--');  
xlabel('Discharge Rate Q (m^3/h)')
ylabel('Pump Head (m)')
title('Pump Delivery Head Characteristics at 2900 RPM')
grid on
legend('Healthy pump')

ポンプの特性に認識可能な変化を生じさせる故障は次のとおりです。

クリアランスの隙間にある摩損
インペラー出口にある摩損
インペラー出口にある堆積物

故障したポンプを解析するため、異なる故障の影響をうけるポンプの速度、トルク、および流量の測定値を収集しました。たとえば、発生した故障がクリアランスリングにある場合、ポンプの測定揚程特性では特性曲線が明らかに変化しています。

load PumpCharacteristicsData Q1 H1 M1  % signals measured for a pump with a large clearance gap
hold on
plot(Q1, H1);  

load PumpCharacteristicsData Q2 H2 M2  % signals measured for a pump with a small clearance gap
plot(Q2, H2);  
legend('Healthy pump','Large clearance','Small clearance')
hold off

トルクと流量特性やその他の故障タイプでも、同様の変化が見られます。

故障診断の自動化のため、観測された変化を定量的な情報に変換します。そのための信頼性のある方法の 1 つは、パラメーター化された曲線を上記にプロットされた揚程と流量の特性データに当てはめることです。ポンプと配管のダイナミクスの支配方程式を使用し、簡略化したトルク関係を使用して、次の方程式が得られます。

$H \approx h_{n n} ω^{2} - h_{n v} ω Q - h_{v v} Q^{2}$

$M_{p} \approx k_{0} ω Q - k_{1} Q^{2} + k_{2} ω^{2}$

$h_{nn}, h_{nv}, h_{vv}, k_{0}, k_{1}, k_{2}$ は推定するパラメーターです。 $ω, Q, H$ 、および $M_{p}$ を測定すると、パラメーターを線形最小二乗法により推定することができます。これらのパラメーターは "特徴" となり、故障検出および診断のアルゴリズムの開発に使用できます。

予備解析: パラメーター値の比較

上記の 3 つの曲線についてパラメーターの推定値を計算しプロットします。 $Q, H$ および $M_{p}$ の測定値をデータとして使用し、 $ω = 2900 R P M$ をポンプの定格回転数として使用します。

w = 2900; % RPM
% Healthy pump
[hnn_0, hnv_0, hvv_0, k0_0, k1_0, k2_0] = linearFit(0, {w, Q0, H0, M0});
% Pump with large clearance
[hnn_1, hnv_1, hvv_1, k0_1, k1_1, k2_1] = linearFit(0, {w, Q1, H1, M1});
% Pump with small clearance
[hnn_2, hnv_2, hvv_2, k0_2, k1_2, k2_2] = linearFit(0, {w, Q2, H2, M2});
X = [hnn_0 hnn_1 hnn_2; hnv_0  hnv_1  hnv_2; hvv_0  hvv_1  hvv_2]';
disp(array2table(X,'VariableNames',{'hnn','hnv','hvv'},...
    'RowNames',{'Healthy','Large Clearance', 'Small Clearance'}))

                          hnn           hnv           hvv   
                       __________    __________    _________

    Healthy            5.1164e-06    8.6148e-05     0.010421
    Large Clearance     4.849e-06     8.362e-05     0.011082
    Small Clearance    5.3677e-06    8.4764e-05    0.0094656

Y = [k0_0 k0_1 k0_2; k1_0  k1_1  k1_2; k2_0  k2_1  k2_2]';
disp(array2table(Y,'VariableNames',{'k0','k1','k2'},...
    'RowNames',{'Healthy','Large Clearance', 'Small Clearance'}))

                           k0           k1           k2    
                       __________    ________    __________

    Healthy            0.00033347    0.016535    2.8212e-07
    Large Clearance    0.00031571    0.016471    3.0285e-07
    Small Clearance    0.00034604    0.015886    2.6669e-07

テーブルは、クリアランスの隙間が大きいと $h_{nn}$ と $k_{0}$ の値が減少し、クリアランスが小さいとノミナル値より大きくなることを示しています。その一方で、 $h_{vv}$ と $k_{2}$ の値はクリアランスの隙間が大きいと増加し、小さい隙間では減少します。 $h_{nv}$ と $k_{1}$ のクリアランスの隙間に対する依存関係はあまり明確ではありません。

不確かさの組み込み

予備解析により、パラメーターの変化によって故障が示される可能性があることがわかりました。しかし、健全なポンプであっても、測定ノイズ、流体の汚濁や粘度の変化、およびポンプを駆動するモーターのすべりとトルクの特性などに起因する測定値の変動が見られます。これらの測定値の変動により、パラメーターの推定値に不確かさが生じます。

故障なしの状態で動作するポンプを、2900 RPM の速度で 10 の吐出スロットルバルブ位置で実行し、このポンプから 5 セットの測定値を収集します。

url = 'https://www.mathworks.com/supportfiles/predmaint/fault-diagnosis-of-centrifugal-pumps-using-steady-state-experiments/FaultDiagnosisData.mat';
websave('FaultDiagnosisData.mat',url);
load FaultDiagnosisData HealthyEnsemble
H = cellfun(@(x)x.Head,HealthyEnsemble,'uni',0);
Q = cellfun(@(x)x.Discharge,HealthyEnsemble,'uni',0);
plot(cat(2,Q{:}),cat(2,H{:}),'k.')
title('Pump Head Characteristics Ensemble for 5 Test Runs')
xlabel('Flow rate (m^3/hed)')
ylabel('Pump head (m)')

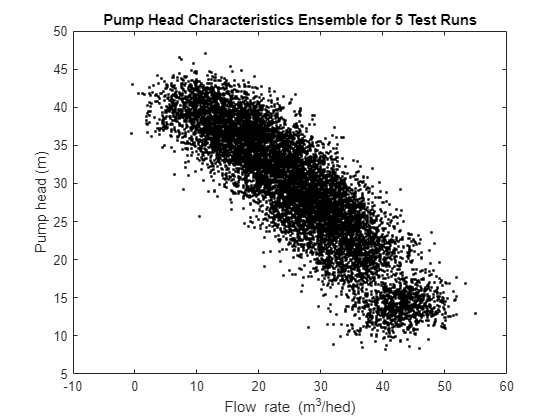
このプロットは、健全なポンプであっても現実的な状態下においては特性が変動することを示します。故障診断を信頼できるものにするには、これらの変動を考慮する必要があります。次の節では、ノイズを含むデータのための故障検出および特定の手法について説明します。

異常の検出

多くの場合、利用できる測定値は健全なマシンのものに限られています。その場合には、利用可能な測定値を使用して、パラメーターベクトルの平均値と共分散でカプセル化された健全な状態の統計的な記述を作成することができます。テストポンプの測定値をノミナルの統計と比較し、テストポンプが健全なポンプである可能性があるかどうかをテストできます。故障したポンプは、検出特性のビューにおいて異常として検出されることが予想されます。

ポンプの揚程およびトルクパラメーターの平均と共分散を推定します。

load FaultDiagnosisData HealthyEnsemble
[HealthyTheta1, HealthyTheta2] = linearFit(1, HealthyEnsemble);
meanTheta1 = mean(HealthyTheta1,1);
meanTheta2 = mean(HealthyTheta2,1);
covTheta1  = cov(HealthyTheta1);
covTheta2  = cov(HealthyTheta2);

パラメーターの不確かさを 74% の信頼領域で可視化します。これは、2 標準偏差に相当します ( $\sqrt{c h i 2 i n v (0.74, 3)} \approx 2$ )。詳細については、補助関数 helperPlotConfidenceEllipsoid を参照してください。

% Confidence ellipsoid for pump head parameters
f = figure;
f.Position(3) = f.Position(3)*2;
subplot(121)
helperPlotConfidenceEllipsoid(meanTheta1,covTheta1,2,0.6);   
xlabel('hnn')
ylabel('hnv')
zlabel('hvv')
title('2-sd Confidence Ellipsoid for Pump Head Parameters')
hold on

% Confidence ellipsoid for pump torque parameters
subplot(122)
helperPlotConfidenceEllipsoid(meanTheta2,covTheta2,2,0.6); 
xlabel('k0')
ylabel('k1')
zlabel('k2')
title('2-sd Confidence Ellipsoid for Pump Torque Parameters')
hold on

グレーの楕円は健全なポンプパラメーターの信頼領域を示します。健全な領域と比較するために、ラベル付けされていないテストデータを読み込みます。

load FaultDiagnosisData TestEnsemble

TestEnsemble は、さまざまなバルブ位置におけるポンプ速度、トルク、揚程、および流量の測定値のセットを含みます。すべての測定値は、大きさの異なるクリアランスの隙間の故障を含みます。

% Test data preview
disp(TestEnsemble{1}(1:5,:)) % first 5 measurement rows from the first ensemble member

      Time       Run    ValvePosition    Speed      Head     Discharge    Torque 
    _________    ___    _____________    ______    ______    _________    _______

    180 sec       1          10          3034.6    12.367     35.339      0.35288
    180.1 sec     1          10          2922.1    9.6762     36.556       4.6953
    180.2 sec     1          10          2636.1    11.168     36.835       9.8898
    180.3 sec     1          10          2717.4    10.562      40.22      -12.598
    180.4 sec     1          10          3183.7     10.55     40.553       14.672

テストパラメーターを計算します。補助関数 linearFit を参照してください。

% TestTheta1: pump head parameters
% TestTheta2: pump torque parameters
[TestTheta1,TestTheta2] = linearFit(1, TestEnsemble);
subplot(121)
plot3(TestTheta1(:,1),TestTheta1(:,2),TestTheta1(:,3),'g*')
view([-42.7 10])
subplot(122)
plot3(TestTheta2(:,1),TestTheta2(:,2),TestTheta2(:,3),'g*')
view([-28.3 18])

緑の星印の各マーカーが 1 つのテストポンプの影響を受けます。信頼限界の外にあるマーカーは外れ値として扱うことができ、中にあるマーカーは健全なポンプからのものか、検出を逃れたものです。特定のポンプからのマーカーが、揚程ビューで異常としてマークされていても、ポンプトルクビューではそうでない場合もあることに注意してください。この理由は、これらのビューで検出される故障の原因が異なるためであるか、圧力とトルクの測定値の基となる信頼性によるものです。

信頼領域を使用した異常検出の定量化

この節では、信頼領域の情報を使用して故障を検出し、その重大度を評価する方法について説明します。この手法では、健全な領域分布の平均または中央値からのテストサンプルの "距離" を計算します。この距離は、その共分散で表される健全なパラメーターデータの正規の "広がり" を基準としなければなりません。関数 MAHAL は、基準サンプルセット (ここでは健全なポンプパラメーターセット) の分布からのテストサンプルのマハラノビス距離を計算します。

ParDist1 = mahal(TestTheta1, HealthyTheta1);  % for pump head parameters

74% の信頼限界 (2 標準偏差) を健全なデータの許容できる変動として仮定した場合、ParDist1 の 2^2 = 4 を超えるすべての値が異常としてタグ付けされることになり、したがって故障状態の動作を示します。

プロットに距離値を追加します。赤いラインは異常なテストサンプルをマークしています。補助関数 helperAddDistanceLines を参照してください。

Threshold = 2;
disp(table((1:length(ParDist1))',ParDist1, ParDist1>Threshold^2,...
    'VariableNames',{'PumpNumber','SampleDistance','Anomalous'}))

    PumpNumber    SampleDistance    Anomalous
    __________    ______________    _________

         1            58.874          true   
         2            24.051          true   
         3             6.281          true   
         4            3.7179          false  
         5             13.58          true   
         6            3.0723          false  
         7            2.0958          false  
         8            4.7127          true   
         9            26.829          true   
        10           0.74682          false

helperAddDistanceLines(1, ParDist1, meanTheta1, TestTheta1, Threshold);

ポンプトルクについても同様です。

ParDist2 = mahal(TestTheta2, HealthyTheta2);  % for pump torque parameters
disp(table((1:length(ParDist2))',ParDist2, ParDist2>Threshold^2,...
    'VariableNames',{'PumpNumber','SampleDistance','Anomalous'}))

    PumpNumber    SampleDistance    Anomalous
    __________    ______________    _________

         1            9.1381          true   
         2            5.4249          true   
         3            3.0565          false  
         4             3.775          false  
         5           0.77961          false  
         6            7.5508          true   
         7            3.3368          false  
         8           0.74834          false  
         9            3.6478          false  
        10            1.0241          false

helperAddDistanceLines(2, ParDist2, meanTheta2, TestTheta2, Threshold);
view([8.1 17.2])

これで、プロットで異常サンプルの検出が示されるだけでなく、その重大度も定量化されます。

1 クラス分類器を使用した異常検出の定量化

異常にフラグを付けるもう 1 つの有効な手法は、健全なパラメーターデータセット用の 1 クラス分類器を作成することです。健全なポンプパラメーターデータを使って SVM 分類器を学習させます。利用される故障ラベルがないので、すべてのサンプルを同じ (健全な) クラスからのものとして扱います。パラメーター $h_{nn}$ および $h_{vv}$ の変化が潜在的な故障を最もよく示唆するので、SVM 分類器の学習にはこれらのパラメーターのみを使用します。

nc = size(HealthyTheta1,1);
rng(2)  % for reproducibility
SVMOneClass1 = fitcsvm(HealthyTheta1(:,[1 3]),ones(nc,1),...
    'KernelScale','auto',...
    'Standardize',true,...
    'OutlierFraction',0.0455);

テストの観測値と決定境界をプロットします。サポートベクトルと潜在的な外れ値にフラグを付けます。補助関数 helperPlotSVM を参照してください。

figure
helperPlotSVM(SVMOneClass1,TestTheta1(:,[1 3]))
title('SVM Anomaly Detection for Pump Head Parameters')
xlabel('hnn')
ylabel('hvv')

外れ値を残りのデータから分離する境界は等高線値が 0 の位置で生じます。これはプロットに "0" でマークされている等位線です。外れ値は赤い円でマークされています。トルクパラメーターについても同様の解析を実行できます。

SVMOneClass2 = fitcsvm(HealthyTheta2(:,[1 3]),ones(nc,1),...
    'KernelScale','auto',...
    'Standardize',true,...
    'OutlierFraction',0.0455);
figure
helperPlotSVM(SVMOneClass2,TestTheta2(:,[1 3]))
title('SVM Anomaly Detection for Torque Parameters')
xlabel('k0')
ylabel('k2')

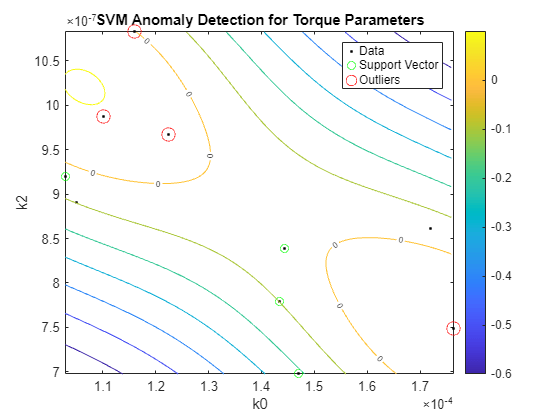
以下に故障特定のコンテキストで説明するように、インペラー出口における摩損や堆積物など、その他のタイプの故障を検出するために同様の解析を行うことが可能です。

定常状態パラメーターを特徴として使用した故障特定

テストシステムにおける故障のタイプに関する情報が利用できる場合には、これを使用して故障の検出だけでなくそのタイプを示すアルゴリズムを作成できます。

A. 尤度比検定法によるクリアランス隙間の故障の区別

クリアランスの隙間の変化を、予想より小さいもの (揚程特性プロットの黄色いライン) と、予想より大きいもの (赤いライン) の 2 つのタイプに分割できます。故障の性質 (大または小) が事前にわかっているクリアランスの隙間の故障を含んだ、ポンプのテストデータセットを読み込みます。これらの故障ラベルを使用して次のモード間で 3-way 分類を実行します。

モード 1: 正常なクリアランスの隙間 (健全動作)
モード 2: 大きいクリアランスの隙間
モード 3: 小さいクリアランスの隙間

url = 'https://www.mathworks.com/supportfiles/predmaint/fault-diagnosis-of-centrifugal-pumps-using-steady-state-experiments/LabeledGapClearanceData.mat';
websave('LabeledGapClearanceData.mat',url);
load LabeledGapClearanceData HealthyEnsemble LargeGapEnsemble SmallGapEnsemble

アンサンブルには 50 の独立した実験からのデータが含まれます。前と同様に定常状態の線形モデルを当てはめて、ポンプの揚程とトルクデータをパラメーター化します。

[HealthyTheta1, HealthyTheta2] = linearFit(1,HealthyEnsemble);
[LargeTheta1, LargeTheta2]     = linearFit(1,LargeGapEnsemble);
[SmallTheta1, SmallTheta2]     = linearFit(1,SmallGapEnsemble);

パラメーターのヒストグラムをプロットし、3 つのモード間に分離可能性があるかどうかをチェックします。関数 histfit を使用して、ヒストグラムおよびそれに対応する当てはめられた正規分布曲線をプロットします。補助関数 helperPlotHistogram を参照してください。

揚程パラメーター:

helperPlotHistogram(HealthyTheta1, LargeTheta1, SmallTheta1, {'hnn','hnv','hvv'})

ヒストグラムは、 $h_{nn}$ による 3 つのモード間の分離可能性が良好である一方、 $h_{nv}, h_{vv}$ パラメーターの確率分布関数 (PDF) はオーバーラップしていることを示しています。

ポンプトルクパラメーター:

helperPlotHistogram(HealthyTheta2, LargeTheta2, SmallTheta2, {'k0','k1','k2'})

トルクパラメーターの場合、個々の分離可能性はあまり良好ではありません。学習済みの 3 モード分類器で利用できる、平均と分散の変動がいくらかあります。PDF で平均または分散がうまく分離している場合、尤度比検定を設計して可能性が最も高いモードにテストデータセットを素早く割り当てることができます。これを、揚程パラメーターについて次に示します。

次のように仮定します。

$Η_{0}$ : 揚程パラメーターが健全なポンプモードに属するという仮説
$Η_{1}$ : 揚程パラメーターが大きなクリアランスの隙間をもつポンプに属するという仮説
$Η_{2}$ : 揚程パラメーターが小さなクリアランスの隙間をもつポンプに属するという仮説

利用できるパラメーターセットをモード予測のテストサンプルとして考えます。予測したモードを、結合 PDF の値が最も高いものに属するとして割り当てます ( $p (H_{0}) > p (H_{1})$ の場合、 $Η_{1}$ ではなく仮説 $Η_{0}$ が選択される)。その後、混同行列での真のモードと予測モードを比較する結果をプロットします。関数 mvnpdf を使用して PDF 値を計算し、関数 confusionmatrix と関数 heatmap を使用して混同行列を可視化します。補助関数 pumpModeLikelihoodTest を参照してください。

% Pump head confusion matrix
figure
pumpModeLikelihoodTest(HealthyTheta1, LargeTheta1, SmallTheta1)

混同プロットは、3 つのモード間の完璧な分離を示しています。これは、 $h_{nn}$ パラメーターのヒストグラム間における明らかな分離を考えれば当然のことです。

% Pump torque confusion matrix
pumpModeLikelihoodTest(HealthyTheta2, LargeTheta2, SmallTheta2)

トルクパラメーターの結果は若干劣っています。それでも、3 つのモードの PDF が著しくオーバーラップしているにもかかわらず、成功率はかなり高く (97%) なっています。これは、PDF 値の計算が位置 (平均) と振幅 (分散) の両方から影響を受けるためです。

B. ツリーバギングを使用した故障モードの複数クラス分類

この節では、さらに多くのモードを分類する必要がある場合に適している、もう 1 つの分類手法について説明します。ポンプの動作における次の故障モードを考えます。

健全な動作
クリアランスの隙間にある摩損
インペラー出口にある少量の堆積物
インペラー入口にある堆積物
インペラー出口にある摩耗
ブレード折損
キャビテーション

計算されたパラメーターは 3 つしかありませんが、7 つの動作モードを区別する必要があるため、分類問題はより困難です。したがって、故障モードごとに推定パラメーターを健全モードと比較するだけでなく、故障モード同士を比較する必要もあり、パラメーター変化の "方向" (値が増えるか減るか) と "振幅" (10% 対 70% の変化) の両方を検討しなければなりません。

ここではこの問題に TreeBagger 分類器を使用する方法を示します。ツリーバガーは、特徴の bootstrap aggregation (バギング) を用いてラベル付きデータを分類する決定木を作成するアンサンブル学習手法です。7 つの動作モードに対して 50 個のラベル付きデータセットが収集されます。データセットごとに揚程パラメーターを推定し、各モードからのパラメーター推定値のサブセットを使用して分類器を学習させます。

url = 'https://www.mathworks.com/supportfiles/predmaint/fault-diagnosis-of-centrifugal-pumps-using-steady-state-experiments/MultipleFaultsData.mat';
websave('MultipleFaultsData.mat',url);
load MultipleFaultsData
% Compute pump head parameters
HealthyTheta = linearFit(1, HealthyEnsemble);
Fault1Theta  = linearFit(1, Fault1Ensemble);
Fault2Theta  = linearFit(1, Fault2Ensemble);
Fault3Theta  = linearFit(1, Fault3Ensemble);
Fault4Theta  = linearFit(1, Fault4Ensemble);
Fault5Theta  = linearFit(1, Fault5Ensemble);
Fault6Theta  = linearFit(1, Fault6Ensemble);

% Generate labels for each mode of operation
Label = {'Healthy','ClearanceGapWear','ImpellerOutletDeposit',...
    'ImpellerInletDeposit','AbrasiveWear','BrokenBlade','Cavitation'};
VarNames = {'hnn','hnv','hvv','Condition'};
% Assemble results in a table with parameters and corresponding labels 
N = 50; 
T0 = [array2table(HealthyTheta),repmat(Label(1),[N,1])];
T0.Properties.VariableNames = VarNames;
T1 = [array2table(Fault1Theta), repmat(Label(2),[N,1])];
T1.Properties.VariableNames = VarNames;
T2 = [array2table(Fault2Theta), repmat(Label(3),[N,1])];
T2.Properties.VariableNames = VarNames;
T3 = [array2table(Fault3Theta), repmat(Label(4),[N,1])];
T3.Properties.VariableNames = VarNames;
T4 = [array2table(Fault4Theta), repmat(Label(5),[N,1])];
T4.Properties.VariableNames = VarNames;
T5 = [array2table(Fault5Theta), repmat(Label(6),[N,1])];
T5.Properties.VariableNames = VarNames;
T6 = [array2table(Fault6Theta), repmat(Label(7),[N,1])];
T6.Properties.VariableNames = VarNames;

% Stack all data
% Use 30 out of 50 datasets for model creation
TrainingData = [T0(1:30,:);T1(1:30,:);T2(1:30,:);T3(1:30,:);T4(1:30,:);T5(1:30,:);T6(1:30,:)];

% Create an ensemble Mdl of 20 decision trees for predicting the 
% labels using the parameter values
rng(3) % for reproducibility
Mdl = TreeBagger(20, TrainingData, 'Condition',...
   'OOBPrediction','on',...
   'OOBPredictorImportance','on')

Mdl = 
  TreeBagger
Ensemble with 20 bagged decision trees:
                    Training X:              [210x3]
                    Training Y:              [210x1]
                        Method:       classification
                 NumPredictors:                    3
         NumPredictorsToSample:                    2
                   MinLeafSize:                    1
                 InBagFraction:                    1
         SampleWithReplacement:                    1
          ComputeOOBPrediction:                    1
 ComputeOOBPredictorImportance:                    1
                     Proximity:                   []
                    ClassNames:  'AbrasiveWear'   'BrokenBlade'    'Cavitation' 'ClearanceGapWear'       'Healthy' 'ImpellerInletDeposit' 'ImpellerOutletDeposit'

  Properties, Methods

out-of-bag 観測値の誤分類確率を決定木の数の関数として調査することにより、TreeBagger モデルの性能を計算できます。

% Compute out of bag error
figure
plot(oobError(Mdl))
xlabel('Number of trees')
ylabel('Misclassification probability')

最後に、決定木の作成に使用されなかったテストサンプルに対し、モデルの予測性能を計算します。

ValidationData = [T0(31:50,:);T1(31:50,:);T2(31:50,:);T3(31:50,:);T4(31:50,:);T5(31:50,:);T6(31:50,:)];
PredictedClass = predict(Mdl,ValidationData);
E = zeros(1,7);
% Healthy data misclassification
E(1) = sum(~strcmp(PredictedClass(1:20), Label{1}));
% Clearance gap fault misclassification
E(2) = sum(~strcmp(PredictedClass(21:40), Label{2}));
% Impeller outlet deposit fault misclassification
E(3) = sum(~strcmp(PredictedClass(41:60), Label{3}));
% Impeller inlet deposit fault misclassification
E(4) = sum(~strcmp(PredictedClass(61:80), Label{4}));
% Abrasive wear fault misclassification
E(5) = sum(~strcmp(PredictedClass(81:100), Label{5}));
% Broken blade fault misclassification
E(6) = sum(~strcmp(PredictedClass(101:120), Label{6}));
% Cavitation fault misclassification
E(7) = sum(~strcmp(PredictedClass(121:140), Label{7}));
figure
bar(E/20*100)
xticklabels(Label)
set(gca,'XTickLabelRotation',45)
ylabel('Misclassification (%)')

プロットは、摩耗とブレード折損の故障が検証サンプルの 30% で誤分類されることを示しています。予測されたラベルをさらに詳しく調べると、誤分類されたケースでは、'AbrasiveWear' と 'BrokenBlade' のラベルが互いに混同されただけであることがわかります。これは、この分類器ではこれらの故障カテゴリの症状を十分に区別できないことを示唆しています。

まとめ

設計の優れた故障診断手法によって、サービスのダウンタイムとコンポーネントの交換費用を最小限に抑えることで運用コストを節約できます。この手法は、稼働するマシンのダイナミクスに関する適切な知識があると有利で、これとセンサー測定値を組み合わせて使用して、異なる種類の故障を検出し特定します。

この例では、定常状態実験に基づく故障検出と特定を行うパラメトリックな方法を説明しました。この方法は、システムダイナミクスの慎重なモデル化と、故障診断アルゴリズム設計のための特徴としてのパラメーター (またはその変換) の使用を必要とします。パラメーターは、異常検出器の学習と、尤度比検定の実行および複数クラス分類器の学習に使用しました。

実際のポンプテストに分類手法を利用する方法

故障診断ワークフローの概要を次に示します。

テストポンプをその定格速度で運転します。吐出バルブをさまざまな設定にして流量を制御します。バルブの位置ごとにポンプ速度、流量、圧力差、およびトルクを書き留めます。
揚程およびポンプトルクの特性 (定常状態) 方程式のためのパラメーターを推定します。
不確かさ/ノイズが少なくパラメーターの推定値に信頼性がある場合、推定したパラメーターをそのノミナル値と直接比較できます。その相対振幅は故障の性質を示します。
一般的なノイズを含む状況では、最初に異常検出手法を使ってシステム内に故障が 1 つでもあるかどうかをチェックします。これは、推定したパラメーター値を健全なポンプの履歴データベースから得た平均と共分散の値に比較することによって迅速に実行できます。
故障が示唆される場合、故障分類手法 (たとえば尤度比検定や分類器の出力など) を用いて、最も可能性の高い原因を特定します。分類手法の選択は、利用できるセンサーデータ、その信頼性、故障の重大度、および故障モードに関する履歴情報の可用性に依存します。

残差分析に基づく故障診断方法については、残差分析を使用した遠心ポンプの故障診断の例を参照してください。

参考文献

Isermann, Rolf, Fault-Diagnosis Applications.Model-Based Condition Monitoring:Actuators, Drives, Machinery, Plants, Sensors, and Fault-tolerant System, Edition 1, Springer-Verlag Berlin Heidelberg, 2011.

サポート関数

ポンプパラメーターの線形近似

function varargout = linearFit(Form, Data)
%linearFit Linear least squares solution for Pump Head and Torque parameters.
%
% If Form==0, accept separate inputs and return separate outputs. For one experiment only.
% If Form==1, accept an ensemble and return compact parameter vectors. For several experiments (ensemble).
if Form==0
   w = Data{1};
   Q = Data{2};
   H = Data{3};
   M = Data{4};
   n = length(Q);
   if isscalar(w), w = w*ones(n,1); end
   Q = Q(:); H = H(:); M = M(:);
   Predictor = [w.^2, w.*Q, Q.^2];
   Theta1 = Predictor\H;
   hnn =  Theta1(1);
   hnv = -Theta1(2);
   hvv = -Theta1(3);
   Theta2 = Predictor\M;
   k0 =  Theta2(2);
   k1 = -Theta2(3);
   k2 =  Theta2(1);
   varargout = {hnn, hnv, hvv, k0, k1, k2};
else
   H = cellfun(@(x)x.Head,Data,'uni',0);
   Q = cellfun(@(x)x.Discharge,Data,'uni',0);
   M = cellfun(@(x)x.Torque,Data,'uni',0);
   W = cellfun(@(x)x.Speed,Data,'uni',0);
   N = numel(H);

   Theta1 = zeros(3,N);
   Theta2 = zeros(3,N);
   
   for kexp = 1:N
      Predictor = [W{kexp}.^2, W{kexp}.*Q{kexp}, Q{kexp}.^2];
      X1 = Predictor\H{kexp};
      hnn =  X1(1);
      hnv = -X1(2);
      hvv = -X1(3);
      X2 = Predictor\M{kexp};
      k0 =  X2(2);
      k1 = -X2(3);
      k2 =  X2(1);
      
      Theta1(:,kexp) = [hnn; hnv; hvv];
      Theta2(:,kexp) = [k0; k1; k2];
   end
   varargout = {Theta1', Theta2'};
end
end

メンバーシップ尤度検定

function pumpModeLikelihoodTest(HealthyTheta, LargeTheta, SmallTheta)
%pumpModeLikelihoodTest Generate predictions based on PDF values and plot confusion matrix.

m1 = mean(HealthyTheta);
c1 = cov(HealthyTheta);
m2 = mean(LargeTheta);
c2 = cov(LargeTheta);
m3 = mean(SmallTheta);
c3 = cov(SmallTheta);

N = size(HealthyTheta,1);

% True classes
% 1: Healthy: group label is 1.
X1t = ones(N,1);
% 2: Large gap: group label is 2.
X2t = 2*ones(N,1);
% 3: Small gap: group label is 3.
X3t = 3*ones(N,1);

% Compute predicted classes as those for which the joint PDF has the maximum value.
X1 = zeros(N,3); 
X2 = zeros(N,3); 
X3 = zeros(N,3); 
for ct = 1:N
   % Membership probability density for healthy parameter sample
   HealthySample  = HealthyTheta(ct,:);
   x1 = mvnpdf(HealthySample, m1, c1);
   x2 = mvnpdf(HealthySample, m2, c2);
   x3 = mvnpdf(HealthySample, m3, c3);
   X1(ct,:) = [x1 x2 x3];
   
   % Membership probability density for large gap pump parameter
   LargeSample  = LargeTheta(ct,:);
   x1 = mvnpdf(LargeSample, m1, c1);
   x2 = mvnpdf(LargeSample, m2, c2);
   x3 = mvnpdf(LargeSample, m3, c3);
   X2(ct,:) = [x1 x2 x3];
   
   % Membership probability density for small gap pump parameter
   SmallSample  = SmallTheta(ct,:);
   x1 = mvnpdf(SmallSample, m1, c1);
   x2 = mvnpdf(SmallSample, m2, c2);
   x3 = mvnpdf(SmallSample, m3, c3);
   X3(ct,:) = [x1 x2 x3];
end

[~,PredictedGroup] = max([X1;X2;X3],[],2);
TrueGroup = [X1t; X2t; X3t];
C = confusionmat(TrueGroup,PredictedGroup);
heatmap(C, ...
    'YLabel', 'Actual condition', ...
    'YDisplayLabels', {'Healthy','Large Gap','Small Gap'}, ...
    'XLabel', 'Predicted condition', ...
    'XDisplayLabels', {'Healthy','Large Gap','Small Gap'}, ...
    'ColorbarVisible','off');
end