ライブ エディター タスクを使用したギア列データの解析およびスペクトル特徴の抽出

この例では、[スペクトル特徴の抽出] ライブ エディター タスクを使用して、ホビーグレード サーボのギア列を駆動することで得られる電流信号からのデータを解析する方法を説明します。例ではまた、故障の検出と特定に活用するために、データからスペクトル特徴を抽出する方法も説明します。

ライブ エディター タスクを使用すると、計算結果への影響を観察しながら、パラメーターと設定を対話的に反復できます。タスクは、表示された結果を実現する MATLAB® コードを自動的に生成します。ライブ エディター タスク全般の詳細については、ライブ スクリプトへの対話型タスクの追加を参照してください。

この例では特に、[スペクトル特徴の抽出] ライブ エディター タスクを使用します。このタスクは、スペクトル データの解析と理解に役立ちます。包括的なインターフェイスを使用することで、さまざまなベアリング、ギアの噛み合い、あるいはハードウェア セットアップの他の部分を表すコンポーネントを追加することができます。これらコンポーネントの物理パラメーターを設定すると、[スペクトル特徴の抽出] ライブ エディター タスクによって、コンポーネントの特性周波数での故障周波数帯域がプロットされます。

パワー スペクトル データを故障帯域のプロットに重ね合わせて、データのさまざまなピークを、コンポーネントの特性周波数と関連付けることができます。この比較では、パワー スペクトル データの変化を、その原因となっている物理コンポーネントまで簡単に遡ることができるため、故障検出と故障特定が行いやすくなります。

タスクでは特性周波数とパワー スペクトル データのプロットに加えて、各特性周波数帯域内でデータのスペクトル メトリクスを生成することができます。各帯域のピーク振幅、ピーク周波数、および帯域パワーが格納された出力メトリクスの table は、潜在的な機械的故障を特徴付けるのに役立ちます。

この例を自分で実行するには、[スペクトル特徴の抽出] ライブ エディター タスクを開き、例で示された設定を複製します。

ハードウェアの概要

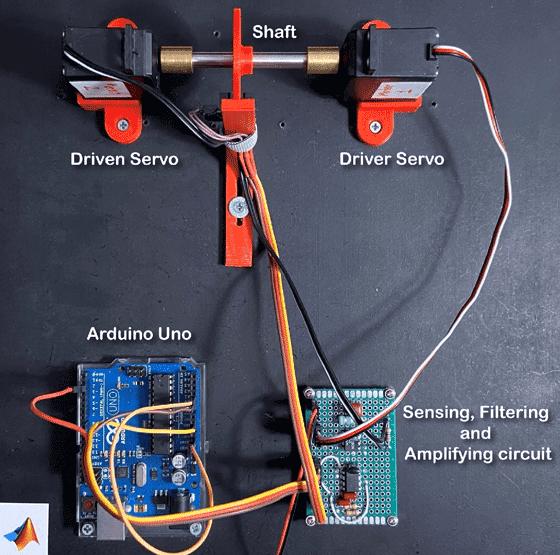
この例では、Futaba の標準的なホビー用サーボ S3003 を連続回転用に改造したものから電流データを収集しました。サーボは、内部の DC モーターの高い速度を、出力スプラインの高いトルクに変換します。これを可能にするため、サーボは DC モーター、ナイロン製または金属製駆動ギアの組、および制御回路によって構成されます。制御回路は、DC モーターへの電流信号を直接監視するため取り外しました。直径 35 mm、16 スロットのホイールとともに赤外線フォトインタラプタを使用して、サーボの出力スプラインにおけるタコメーター信号を収集しました。ホイールの 16 のスロットは等間隔であり、IR フォトインタラプタはスロット付きホイールの 1 回転につき正確に 16 パルスを発するよう配置しました。サーボとフォトインタラプタは、カスタムで 3 次元プリントしたマウントによって保持しました。

DC モーターは 5 V の定電圧で駆動され、4 組のギアで 278:1 の減速を行うため、スプラインでのシャフト回転数は約 19.5 rpm になりました。2 番目のサーボ モーターは短絡されており、システムの負荷として使用されました。消費電流は、0.5 Ω の抵抗の両端の電圧低下を測定することによってオームの法則を使用して計算されました。電流測定値の変化は小さすぎて検出できないため、AD22050 単電源センサー インターフェイス アンプを使用して電流信号を増幅しました。増幅された電流信号は、MAX7408 アンチエイリアシング 5 次楕円ローパス フィルターを使用して平滑化とノイズ除去を行ってから、アナログ デジタル コンバーター (ADC) を介して Arduino® Uno に送られました。

フロー チャートに示すように、電流信号はまずアンプで増幅されてから、アンチエイリアシング ローパス フィルターでフィルター処理されます。Arduino Uno は、ADC を通して送られた電流信号を 1.5 kHz でサンプリングし、タコメーターのパルスとともにシリアル データとして 115,200 bps のボー レートでコンピューターにストリーミングしました。MATLAB スクリプトが Arduino Uno からシリアル データを取得し、前処理を行って、.MAT ファイルに書き込みました。その後、[スペクトル特徴の抽出] ライブ エディター タスクを使用して、スペクトル メトリクスを抽出しました。

サーボのギア列

この図に示すように、Futaba の S3003 サーボは 4 組のナイロン製ギアで構成されています。DC モーター シャフト上のピニオン P1 は段付きギア G1 と噛み合います。ピニオン P2 は段付きギア G1 の成形部分であり、段付きギア G2 と噛み合います。ピニオン P3 はギア G2 の成形部分であり、段付きギア G3 と噛み合います。ピニオン P4 は G3 の成形の一部分であり、出力スプラインに取り付けられた最終ギア G4 と噛み合います。G1 と P2、G2 と P3、G3 と P4 の段付きギアの組は自由回転ギアです $-$ すなわち、これらは各シャフトに固定されていません。駆動ギアの組は 278:1 の減速を行い、モーターを 5 V で駆動するとき、5414.7 rpm のモーター速度を約 19.5 rpm の出力スプラインに減速します。次の表に、歯数と、各ギア噛み合いにおける出力速度、ギアの噛み合い周波数、累積ギア減速比の理論値を示します。

データの前処理

ファイル servoData.mat には、サーボからのデータに対応する 2 つの timetable が含まれています。一方の timetable には健全状態のデータが含まれ、2 つ目の timetable には故障状態のデータが含まれています。各データセットには、1500 Hz でサンプリングされた約 11 秒のデータが含まれます。

データを読み込みます。

load('servoData.mat', 'healthyData', 'faultyData')
healthyData

healthyData=16384×2 timetable
         Time         MotorCurrent    TachoPulse
    ______________    ____________    __________

    0 sec                307.62           1     
    0.00066667 sec       301.27           1     
    0.0013333 sec        309.08           1     
    0.002 sec            315.92           1     
    0.0026667 sec         304.2           1     
    0.0033333 sec        311.04           1     
    0.004 sec            311.52           1     
    0.0046667 sec        305.18           1     
    0.0053333 sec        315.43           0     
    0.006 sec            310.06           0     
    0.0066667 sec        305.66           0     
    0.0073333 sec        310.55           0     
    0.008 sec            304.69           0     
    0.0086667 sec        310.55           0     
    0.0093333 sec        310.06           0     
    0.01 sec              299.8           0     
      ⋮

faultyData

faultyData=16384×2 timetable
         Time         MotorCurrent    TachoPulse
    ______________    ____________    __________

    0 sec                313.48           0     
    0.00066667 sec        304.2           0     
    0.0013333 sec        303.22           0     
    0.002 sec            319.34           0     
    0.0026667 sec         304.2           0     
    0.0033333 sec        303.22           0     
    0.004 sec            319.82           0     
    0.0046667 sec        303.22           0     
    0.0053333 sec        306.64           0     
    0.006 sec            321.29           0     
    0.0066667 sec        303.71           0     
    0.0073333 sec        308.11           0     
    0.008 sec            319.34           0     
    0.0086667 sec        301.76           0     
    0.0093333 sec        309.08           0     
    0.01 sec             319.34           0     
      ⋮

各 timetable には、モーターの電流の記された 1 列と、サーボ セットアップからのタコメーターのパルスが記された 1 列が含まれています。[スペクトル特徴の抽出] ライブ エディター タスクでデータを可視化するために、モーターの電流データのパワー スペクトルを計算します。まず健全状態のデータを検討します。

fs = 1500;
[healthyMagnitudes, healthyFrequencies] = pspectrum(healthyData.MotorCurrent, healthyData.Time);

[スペクトル特徴の抽出] ライブ エディター タスクを使用して、パワー スペクトル データをプロットします。タスクでは、周波数ベクトルに healthyMagnitudes を、パワー スペクトルの振幅に healthyFrequencies を指定します。

高調波故障周波数帯域でのパワー スペクトルのピークの解析

サーボの電流データのパワー スペクトル プロットには、いくつかの顕著なピークが含まれています。これらのピークを、サーボ セットアップの回転シャフトと関連付けることができます。さまざまなピークのソースを判定するために、[スペクトル特徴の抽出] ライブ エディター タスクにコンポーネントを追加します。

サーボの最初の回転シャフトを表すコンポーネントを追加するには、コンポーネントの名前を入力し、そのタイプに [カスタム] を選択して、[追加] を押します。上記の表の出力回転数を使用して、シャフト コンポーネントの周波数を選択します。出力回転数は、出力シャフトの測定された回転数と、セットアップでの既知のギア減速に基づいて計算されたものです。

最初のシャフトの周波数は 90.24 Hz です。シャフト コンポーネントの周波数値を設定した後は、故障周波数帯域が、90 Hz 付近でパワー スペクトル データのピークの 1 つとオーバーラップしていることに注意してください。したがって、このピークは主に最初のシャフトと関連付けることができます。最初のシャフトの基本周波数の高調波をさらにいくつか加えると、データの他のピークとオーバーラップする故障周波数帯域がさらに作成されます。高調波周波数帯域は基本周波数の整数倍を中心としており、やはり同じコンポーネントと関連付けることができます。最初のシャフトの高調波がベクトル [1 2 3 4 5 6] となるように設定し、故障帯域がほとんどの周波数範囲に広がるようにします。最初のシャフトは最も高い周波数で回転するため、高めの周波数にあるパワー スペクトルのピークはこのシャフトの高調波によるものです。

13 Hz や 29 Hz 付近のような、比較的小さいパワー スペクトルのピークに対応するには、2 番目の回転シャフトのコンポーネントを追加します。このコンポーネントもカスタム コンポーネントであり、その基本周波数は 14.56 Hz です。高周波数のピークのほとんどが最初のシャフトの高調波で概ね対応されているため、2 番目のシャフトでは、さほど多くの高調波を加える必要はありません。2 番目のシャフトの高調波がベクトル [1 2 3 4] となるように設定します。このシャフト周波数の 1 番目、2 番目、4 番目の高調波が、パワー スペクトル プロットのピークとうまく合致します。ただし、3 番目の高調波はデータにおいてあまり顕著でないため、この高調波を含める必要はありません。2 番目のシャフトの高調波がベクトル [1 2 4] となるよう変更します。

2 番目のシャフトと同様に、3 番目の回転シャフトのコンポーネントを追加します。このコンポーネントの基本周波数は、表でわかるように 2.91 Hz です。最初の 4 つの高調波から始めて、それらがデータの顕著なピークと合致するかどうかを判定します。3 番目のシャフトの 3 番目の高調波が、8 Hz 付近でパワー スペクトルのスパイクと一致することに注意してください。他の高調波はあまり顕著ではなく、削除することができます。パワー スペクトルの周波数分解能では、低めの周波数を識別できないという可能性もあります。3 番目のシャフト コンポーネントの高調波を、3 番目の高調波のみに設定します。

残りのシャフトの出力回転数も周波数が低く、パワー スペクトルの周波数分解能からは識別できない可能性があるため、モーターの電流データの主なピークを解析するにあたって、これらのシャフトのコンポーネントを追加する必要はありません。

側波帯のピークの解析

タスクのプロットにズームインすると、パワー スペクトル データには、いくつかの主要ピークの横にサイド ピークが含まれていることがわかります。たとえば、76 Hz と 104 Hz 付近の比較的小さなサイド ピークが、90 Hz のピークを囲んでいます。これらのピークはおそらく、最初のシャフト コンポーネントの側波帯と関連しています。側波帯は、2 番目の関連周波数のソースが主要な高調波周波数のソースに影響を与えることで発生します。サーボ セットアップの場合、この観察は、各シャフトの側波帯がギア列の隣のシャフトによって生じているという推定につながります。

最初の 2 つのシャフト コンポーネントを編集して、それらの最初の側波帯を含めます。最初のシャフトの側波帯分離値は 2 番目のシャフトの定格出力周波数 14.56 Hz と等しくする必要があります。

同様に、2 番目のシャフトの側波帯分離値は 3 番目のシャフトの定格周波数 2.91 Hz と等しくする必要があります。プロットに再度ズームインすると、多くの新たな側波帯が、データ内のサイド ピークと良好にオーバーラップしていることがわかります。これは、0 Hz ～ 120 Hz のような低い周波数で確認しやすくなっています。

スペクトル メトリクスの抽出による故障の検出

[スペクトル特徴の抽出] ライブ エディター タスクでは、故障周波数範囲におけるパワー スペクトル データのさまざまなスペクトル メトリクスが生成されます。各故障周波数帯域のピーク振幅、ピーク周波数、および帯域パワーと、すべての故障周波数帯域の合計帯域パワーを計算します。

load('dataSample1.mat')
spectralMetrics_healthy

spectralMetrics_healthy=1×85 table
    PeakAmplitude1    PeakFrequency1    BandPower1    PeakAmplitude2    PeakFrequency2    BandPower2    PeakAmplitude3    PeakFrequency3    BandPower3    PeakAmplitude4    PeakFrequency4    BandPower4    PeakAmplitude5    PeakFrequency5    BandPower5    PeakAmplitude6    PeakFrequency6    BandPower6    PeakAmplitude7    PeakFrequency7    BandPower7    PeakAmplitude8    PeakFrequency8    BandPower8    PeakAmplitude9    PeakFrequency9    BandPower9    PeakAmplitude10    PeakFrequency10    BandPower10    PeakAmplitude11    PeakFrequency11    BandPower11    PeakAmplitude12    PeakFrequency12    BandPower12    PeakAmplitude13    PeakFrequency13    BandPower13    PeakAmplitude14    PeakFrequency14    BandPower14    PeakAmplitude15    PeakFrequency15    BandPower15    PeakAmplitude16    PeakFrequency16    BandPower16    PeakAmplitude17    PeakFrequency17    BandPower17    PeakAmplitude18    PeakFrequency18    BandPower18    PeakAmplitude19    PeakFrequency19    BandPower19    PeakAmplitude20    PeakFrequency20    BandPower20    PeakAmplitude21    PeakFrequency21    BandPower21    PeakAmplitude22    PeakFrequency22    BandPower22    PeakAmplitude23    PeakFrequency23    BandPower23    PeakAmplitude24    PeakFrequency24    BandPower24    PeakAmplitude25    PeakFrequency25    BandPower25    PeakAmplitude26    PeakFrequency26    BandPower26    PeakAmplitude27    PeakFrequency27    BandPower27    PeakAmplitude28    PeakFrequency28    BandPower28    TotalBandPower
    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    ______________

       0.018807           77.106         0.044031        0.66362            90.842          2.2909        0.0077426           104.58         0.026419       0.0019168           168.13        0.0076763        0.038096           182.6          0.13879        0.0034959           192.86         0.013926        0.026784           258.24         0.11461         0.19204            270.7          0.68298         0.033746           284.07         0.12342         0.0026495           347.62          0.0099187        0.0048234           360.81          0.020787         0.0022197           375.64          0.0086089        0.018193            435.53          0.074193         0.041176            449.08           0.12665         0.018563            467.22          0.069274          0.96653            526.01           3.7305           0.91167            539.19           3.1072           0.29483            558.24           1.0806           1.0344             11.905           0.75499          4.2123             14.286           3.0377          0.076126            17.399          0.078413         0.037838            26.557          0.038039          0.75323            29.121           0.63973         0.010537            32.234          0.010979         0.0058568           55.311          0.006088          0.01419            58.425          0.011768         0.0033215           61.355          0.0034384         0.51018            8.7912           0.27612          16.528    

これらのメトリクスは、サーボ セットアップで故障を検出するのに役立つ可能性があります。パワー スペクトル データの大きな変化は、多くの場合、何らかのコンポーネントが変化しつつあるか、故障しかけていることを示します。ピーク周波数のいずれかにシフトがある場合、またはピーク振幅が時間とともに大きく下がる場合、これは故障の兆候かもしれません。

このシナリオを調べるには、故障データ セットのパワー スペクトル データを計算します。

[faultyMagnitudes, faultyFrequencies] = pspectrum(faultyData.MotorCurrent, faultyData.Time);

タスク内で故障データのスペクトルをプロットし、サーボ セットアップの測定された出力回転数に基づき、シャフト コンポーネントの基本周波数と側波帯分離値を調整します。

Fs = 1500; % 1500 Hz
[outputSpeed,t] = tachorpm(faultyData.TachoPulse,Fs,'PulsesPerRev',16,'FitType','linear');
meanOutputSpeed = mean(outputSpeed)/60 % convert from rpm to Hz

meanOutputSpeed = 
0.3150

shaft4Speed = meanOutputSpeed * 41 / 16 % 16 pinion teeth, 41 gear teeth

shaft4Speed = 
0.8072

shaft3Speed = shaft4Speed * 35 / 10 % 10 pinion teeth, 35 gear teeth

shaft3Speed = 
2.8251

shaft2Speed = shaft3Speed * 50 / 10 % 10 pinion teeth, 50 gear teeth

shaft2Speed = 
14.1254

shaft1Speed = shaft2Speed * 62 / 10 % 10 pinion teeth, 62 gear teeth

shaft1Speed = 
87.5772

最初のシャフト コンポーネントでは、shaft1Speed を基本周波数として、また shaft2Speed を側波帯分離として使用します。2 番目のシャフト コンポーネントでは、shaft2Speed を基本周波数として、また shaft3Speed を側波帯分離として使用します。3 番目のシャフト コンポーネントでは、shaft3Speed を基本周波数として使用します。

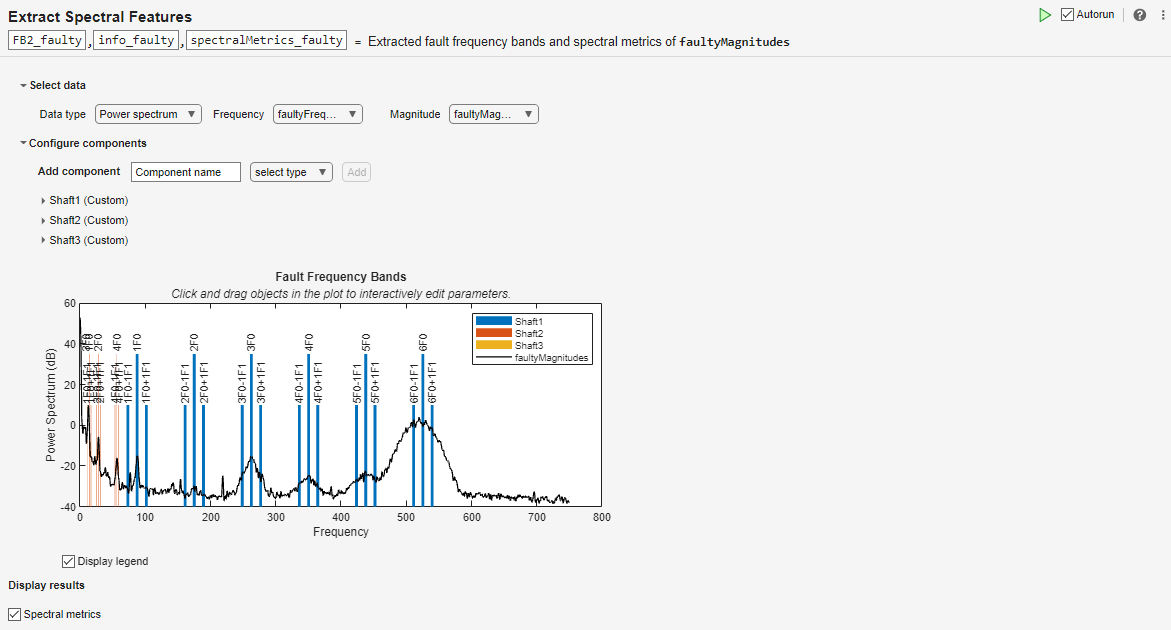
故障パワー スペクトル データの可視化で確認できるように、ピークのいくつかは振幅が小さくなっています。たとえば、健全状態のデータセットにおいて 180 Hz 付近で最初のシャフトの 2 番目の高調波と合致していたピークは、故障状態のデータセットではほとんど無視できます。このピークは最初のシャフトに関連している可能性が高いと先ほど判断していたので、これは、最初のシャフトに故障の可能性があることを示しています。スペクトル メトリクスの table をさらに調べると、ピーク周波数、ピーク振幅、および帯域パワーについてより詳しい情報が得られます。

spectralMetrics_faulty

spectralMetrics_faulty=1×85 table
    PeakAmplitude1    PeakFrequency1    BandPower1    PeakAmplitude2    PeakFrequency2    BandPower2    PeakAmplitude3    PeakFrequency3    BandPower3    PeakAmplitude4    PeakFrequency4    BandPower4    PeakAmplitude5    PeakFrequency5    BandPower5    PeakAmplitude6    PeakFrequency6    BandPower6    PeakAmplitude7    PeakFrequency7    BandPower7    PeakAmplitude8    PeakFrequency8    BandPower8    PeakAmplitude9    PeakFrequency9    BandPower9    PeakAmplitude10    PeakFrequency10    BandPower10    PeakAmplitude11    PeakFrequency11    BandPower11    PeakAmplitude12    PeakFrequency12    BandPower12    PeakAmplitude13    PeakFrequency13    BandPower13    PeakAmplitude14    PeakFrequency14    BandPower14    PeakAmplitude15    PeakFrequency15    BandPower15    PeakAmplitude16    PeakFrequency16    BandPower16    PeakAmplitude17    PeakFrequency17    BandPower17    PeakAmplitude18    PeakFrequency18    BandPower18    PeakAmplitude19    PeakFrequency19    BandPower19    PeakAmplitude20    PeakFrequency20    BandPower20    PeakAmplitude21    PeakFrequency21    BandPower21    PeakAmplitude22    PeakFrequency22    BandPower22    PeakAmplitude23    PeakFrequency23    BandPower23    PeakAmplitude24    PeakFrequency24    BandPower24    PeakAmplitude25    PeakFrequency25    BandPower25    PeakAmplitude26    PeakFrequency26    BandPower26    PeakAmplitude27    PeakFrequency27    BandPower27    PeakAmplitude28    PeakFrequency28    BandPower28    TotalBandPower
    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    ______________

      0.0011027           75.641         0.003537        0.032586           88.095         0.095873       0.00095284          101.47         0.00395        0.00041757          158.97        0.0016883       0.0010558           174.73        0.0038404       0.00041803          190.11        0.0018164       0.0051769           249.27         0.017515        0.02861            261.54         0.12024        0.0050995           274.91         0.015488        0.0014899           336.08          0.0062536        0.0034166           350.37           0.0151          0.0014213           363.19          0.0049667        0.0022729           423.63          0.0092143        0.0058396           437.36          0.020548         0.0031547           450.37          0.010476          1.9385             511.36           6.3395           1.3398             523.81           5.1888           0.79239            539.38           2.9425           0.99793            11.538           0.82466          2.7276             13.919           1.9334           0.03098            17.033           0.03294         0.019366            25.641          0.018542          0.27042            28.205           0.26876         0.0056307           31.136          0.0060665        0.0029552           54.029          0.0028713        0.024583            56.593          0.025096         0.002738            58.974          0.0027415         0.74611            8.4249           0.40382          18.32     

ライブ エディター タスクでスペクトル データを更新する代わりに、自動生成された MATLAB コードを使用して、故障データのスペクトル メトリクスを決定することもできます。以下のコードは、ライブ エディター タスクを使用して健全状態のスペクトル メトリクスを生成した時に自動生成されたものです。コードを実行します。

% Generate the fault bands and information for each component
[FB_Shaft1, info_Shaft1] = faultBands(90.24, 1:6, 14.56, 0:1);
[FB_Shaft2, info_Shaft2] = faultBands(14.56, [1 2 4], 2.91, 0:1);
[FB_Shaft3, info_Shaft3] = faultBands(2.91, 3);

% Combine the fault bands of each component
FB_healthy = [FB_Shaft1; ...
		FB_Shaft2; ...
		FB_Shaft3];

% Combine the information regarding the fault bands of each component
info_healthy.Centers = [info_Shaft1.Centers, ...
		info_Shaft2.Centers, ...
		info_Shaft3.Centers];
info_healthy.Labels = [info_Shaft1.Labels, ...
		info_Shaft2.Labels, ...
		info_Shaft3.Labels];
info_healthy.FaultGroups = [info_Shaft1.HarmonicGroups, ...
		info_Shaft2.HarmonicGroups, ...
		info_Shaft3.HarmonicGroups];

% Clear temporary outputs from the workspace
clear FB_Shaft1 info_Shaft1;
clear FB_Shaft2 info_Shaft2;
clear FB_Shaft3 info_Shaft3;

% Compute fault band metrics of the power spectrum healthyMagnitudes
spectralMetrics_healthy = faultBandMetrics(healthyMagnitudes, healthyFrequencies, FB_healthy)

spectralMetrics_healthy=1×85 table
    PeakAmplitude1    PeakFrequency1    BandPower1    PeakAmplitude2    PeakFrequency2    BandPower2    PeakAmplitude3    PeakFrequency3    BandPower3    PeakAmplitude4    PeakFrequency4    BandPower4    PeakAmplitude5    PeakFrequency5    BandPower5    PeakAmplitude6    PeakFrequency6    BandPower6    PeakAmplitude7    PeakFrequency7    BandPower7    PeakAmplitude8    PeakFrequency8    BandPower8    PeakAmplitude9    PeakFrequency9    BandPower9    PeakAmplitude10    PeakFrequency10    BandPower10    PeakAmplitude11    PeakFrequency11    BandPower11    PeakAmplitude12    PeakFrequency12    BandPower12    PeakAmplitude13    PeakFrequency13    BandPower13    PeakAmplitude14    PeakFrequency14    BandPower14    PeakAmplitude15    PeakFrequency15    BandPower15    PeakAmplitude16    PeakFrequency16    BandPower16    PeakAmplitude17    PeakFrequency17    BandPower17    PeakAmplitude18    PeakFrequency18    BandPower18    PeakAmplitude19    PeakFrequency19    BandPower19    PeakAmplitude20    PeakFrequency20    BandPower20    PeakAmplitude21    PeakFrequency21    BandPower21    PeakAmplitude22    PeakFrequency22    BandPower22    PeakAmplitude23    PeakFrequency23    BandPower23    PeakAmplitude24    PeakFrequency24    BandPower24    PeakAmplitude25    PeakFrequency25    BandPower25    PeakAmplitude26    PeakFrequency26    BandPower26    PeakAmplitude27    PeakFrequency27    BandPower27    PeakAmplitude28    PeakFrequency28    BandPower28    TotalBandPower
    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    ______________

       0.018807           77.106         0.044031        0.66362            90.842          2.2909        0.0077426           104.58         0.026419       0.0019168           168.13        0.0076763        0.038096           182.6          0.13879        0.0034959           192.86         0.013926        0.026784           258.24         0.11461         0.19204            270.7          0.68298         0.033746           284.07         0.12342         0.0026495           347.62          0.0099187        0.0048234           360.81          0.020787         0.0022197           375.64          0.0086089        0.018193            435.53          0.074193         0.041176            449.08           0.12665         0.018563            467.22          0.069274          0.96653            526.01           3.7305           0.91167            539.19           3.1072           0.29483            558.24           1.0806           1.0344             11.905           0.75499          4.2123             14.286           3.0377          0.076126            17.399          0.078413         0.037838            26.557          0.038039          0.75323            29.121           0.63973         0.010537            32.234          0.010979         0.0058568           55.311          0.006088          0.01419            58.425          0.011768         0.0033215           61.355          0.0034384         0.51018            8.7912           0.27612          16.528    

このコードは、新しい故障状態のデータセット用に簡単に調整できます。

% Generate the fault bands and information for each component
[FB_Shaft1, info_Shaft1] = faultBands(shaft1Speed, 1:6, shaft2Speed, 0:1);
[FB_Shaft2, info_Shaft2] = faultBands(shaft2Speed, [1 2 4], shaft3Speed, 0:1);
[FB_Shaft3, info_Shaft3] = faultBands(shaft3Speed, 3);

% Combine the fault bands of each component
FB_faulty = [FB_Shaft1; ...
		FB_Shaft2; ...
		FB_Shaft3];

% Combine the information regarding the fault bands of each component
info_faulty.Centers = [info_Shaft1.Centers, ...
		info_Shaft2.Centers, ...
		info_Shaft3.Centers];
info_faulty.Labels = [info_Shaft1.Labels, ...
		info_Shaft2.Labels, ...
		info_Shaft3.Labels];
info_faulty.FaultGroups = [info_Shaft1.HarmonicGroups, ...
		info_Shaft2.HarmonicGroups, ...
		info_Shaft3.HarmonicGroups];

% Clear temporary outputs from the workspace
clear FB_Shaft1 info_Shaft1;
clear FB_Shaft2 info_Shaft2;
clear FB_Shaft3 info_Shaft3;

% Compute fault band metrics of the power spectrum healthyMagnitudes
spectralMetrics_faulty = faultBandMetrics(faultyMagnitudes, faultyFrequencies, FB_faulty)

spectralMetrics_faulty=1×85 table
    PeakAmplitude1    PeakFrequency1    BandPower1    PeakAmplitude2    PeakFrequency2    BandPower2    PeakAmplitude3    PeakFrequency3    BandPower3    PeakAmplitude4    PeakFrequency4    BandPower4    PeakAmplitude5    PeakFrequency5    BandPower5    PeakAmplitude6    PeakFrequency6    BandPower6    PeakAmplitude7    PeakFrequency7    BandPower7    PeakAmplitude8    PeakFrequency8    BandPower8    PeakAmplitude9    PeakFrequency9    BandPower9    PeakAmplitude10    PeakFrequency10    BandPower10    PeakAmplitude11    PeakFrequency11    BandPower11    PeakAmplitude12    PeakFrequency12    BandPower12    PeakAmplitude13    PeakFrequency13    BandPower13    PeakAmplitude14    PeakFrequency14    BandPower14    PeakAmplitude15    PeakFrequency15    BandPower15    PeakAmplitude16    PeakFrequency16    BandPower16    PeakAmplitude17    PeakFrequency17    BandPower17    PeakAmplitude18    PeakFrequency18    BandPower18    PeakAmplitude19    PeakFrequency19    BandPower19    PeakAmplitude20    PeakFrequency20    BandPower20    PeakAmplitude21    PeakFrequency21    BandPower21    PeakAmplitude22    PeakFrequency22    BandPower22    PeakAmplitude23    PeakFrequency23    BandPower23    PeakAmplitude24    PeakFrequency24    BandPower24    PeakAmplitude25    PeakFrequency25    BandPower25    PeakAmplitude26    PeakFrequency26    BandPower26    PeakAmplitude27    PeakFrequency27    BandPower27    PeakAmplitude28    PeakFrequency28    BandPower28    TotalBandPower
    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    ______________

      0.0011027           75.641         0.003537        0.032586           88.095         0.095873       0.00095284          101.47         0.00395        0.00041757          158.97        0.0016883       0.0010558           174.73        0.0038404       0.00041803          190.11        0.0018164       0.0051769           249.27         0.017515        0.02861            261.54         0.12024        0.0050995           274.91         0.015488        0.0014899           336.08          0.0062536        0.0034166           350.37           0.0151          0.0014213           363.19          0.0049667        0.0022729           423.63          0.0092143        0.0058396           437.36          0.020548         0.0031547           450.37          0.010476          1.9385             511.36           6.3395           1.3398             523.81           5.1888           0.79239            539.38           2.9425           0.99793            11.538           0.82466          2.7276             13.919           1.9334           0.03098            17.033           0.03294         0.019366            25.641          0.018542          0.27042            28.205           0.26876         0.0056307           31.136          0.0060665        0.0029552           54.029          0.0028713        0.024583            56.593          0.025096         0.002738            58.974          0.0027415         0.74611            8.4249           0.40382          18.32     

健全状態と故障状態のスペクトル メトリクスの table を組み合わせることで、スペクトル データのピーク振幅と帯域パワーにおける変化が見えやすくなります。

spectralMetrics_total = [spectralMetrics_healthy; spectralMetrics_faulty]

spectralMetrics_total=2×85 table
    PeakAmplitude1    PeakFrequency1    BandPower1    PeakAmplitude2    PeakFrequency2    BandPower2    PeakAmplitude3    PeakFrequency3    BandPower3    PeakAmplitude4    PeakFrequency4    BandPower4    PeakAmplitude5    PeakFrequency5    BandPower5    PeakAmplitude6    PeakFrequency6    BandPower6    PeakAmplitude7    PeakFrequency7    BandPower7    PeakAmplitude8    PeakFrequency8    BandPower8    PeakAmplitude9    PeakFrequency9    BandPower9    PeakAmplitude10    PeakFrequency10    BandPower10    PeakAmplitude11    PeakFrequency11    BandPower11    PeakAmplitude12    PeakFrequency12    BandPower12    PeakAmplitude13    PeakFrequency13    BandPower13    PeakAmplitude14    PeakFrequency14    BandPower14    PeakAmplitude15    PeakFrequency15    BandPower15    PeakAmplitude16    PeakFrequency16    BandPower16    PeakAmplitude17    PeakFrequency17    BandPower17    PeakAmplitude18    PeakFrequency18    BandPower18    PeakAmplitude19    PeakFrequency19    BandPower19    PeakAmplitude20    PeakFrequency20    BandPower20    PeakAmplitude21    PeakFrequency21    BandPower21    PeakAmplitude22    PeakFrequency22    BandPower22    PeakAmplitude23    PeakFrequency23    BandPower23    PeakAmplitude24    PeakFrequency24    BandPower24    PeakAmplitude25    PeakFrequency25    BandPower25    PeakAmplitude26    PeakFrequency26    BandPower26    PeakAmplitude27    PeakFrequency27    BandPower27    PeakAmplitude28    PeakFrequency28    BandPower28    TotalBandPower
    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    ______________    ______________    __________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    _______________    _______________    ___________    ______________

       0.018807           77.106         0.044031         0.66362           90.842           2.2909        0.0077426          104.58         0.026419        0.0019168          168.13        0.0076763        0.038096            182.6          0.13879        0.0034959          192.86         0.013926        0.026784           258.24          0.11461        0.19204             270.7         0.68298         0.033746           284.07          0.12342        0.0026495           347.62          0.0099187        0.0048234           360.81          0.020787         0.0022197           375.64          0.0086089         0.018193           435.53           0.074193         0.041176           449.08           0.12665          0.018563           467.22          0.069274          0.96653            526.01           3.7305           0.91167            539.19           3.1072           0.29483            558.24           1.0806            1.0344            11.905           0.75499          4.2123             14.286           3.0377          0.076126            17.399          0.078413         0.037838            26.557          0.038039          0.75323            29.121           0.63973          0.010537           32.234           0.010979        0.0058568           55.311           0.006088         0.01419            58.425          0.011768         0.0033215           61.355          0.0034384         0.51018            8.7912           0.27612          16.528    
      0.0011027           75.641         0.003537        0.032586           88.095         0.095873       0.00095284          101.47          0.00395       0.00041757          158.97        0.0016883       0.0010558           174.73        0.0038404       0.00041803          190.11        0.0018164       0.0051769           249.27         0.017515        0.02861            261.54         0.12024        0.0050995           274.91         0.015488        0.0014899           336.08          0.0062536        0.0034166           350.37            0.0151         0.0014213           363.19          0.0049667        0.0022729           423.63          0.0092143        0.0058396           437.36          0.020548         0.0031547           450.37          0.010476           1.9385            511.36           6.3395            1.3398            523.81           5.1888           0.79239            539.38           2.9425           0.99793            11.538           0.82466          2.7276             13.919           1.9334           0.03098            17.033           0.03294         0.019366            25.641          0.018542          0.27042            28.205           0.26876         0.0056307           31.136          0.0060665        0.0029552           54.029          0.0028713        0.024583            56.593          0.025096          0.002738           58.974          0.0027415         0.74611            8.4249           0.40382           18.32    

たとえば、table の PeakAmplitude2 を見ると、パワー スペクトルのピークの振幅が 2.0259 から 0.0829 に落ちています。PeakFrequency2 の値を使用すると、この低下が 90 Hz 付近で発生していることがわかります。2 つのパワー スペクトルを同じ座標軸にプロットして、ライブ エディター タスクの外部で低下を可視化します。

plot(healthyFrequencies,10*log10(healthyMagnitudes),'b-'); % plot in decibels
hold on;
plot(faultyFrequencies,10*log10(faultyMagnitudes),'r-'); % plot in decibels
legend('Healthy','Faulty')
xlabel('Frequency (Hz)')
ylabel('Power Spectrum (dB)')
title('Comparison of Power Spectrums')
hold off;

メトリクスの table に示されたように、90 Hz 付近のピークは振幅が大きく落ちています。どのコンポーネント周波数がこの原因であるかを判定するために、前の [スペクトル特徴の抽出] ライブ エディター タスクを再度確認します。

90 Hz 付近の故障帯域は、最初の回転シャフトの 1 番目の高調波です。したがって、このシャフトで何かが変化しており、故障に傾きつつある可能性があるとわかります。

健全状態と故障状態のパワー スペクトルを一緒にプロットするのは、ピーク振幅の変化を強調させるのに役立つ場合があります。最初のシャフトの 1 番目の高調波に対応する 90 Hz 付近のピークに加え、180 Hz 付近にあるこのシャフトの 2 番目の高調波など、他にもピーク振幅の大きな低下が見られます。後者のピークは、故障状態のデータセットに実質上存在しません。

健全状態のデータと故障状態のデータからのピーク振幅は、棒グラフを使用して比較することもできます。

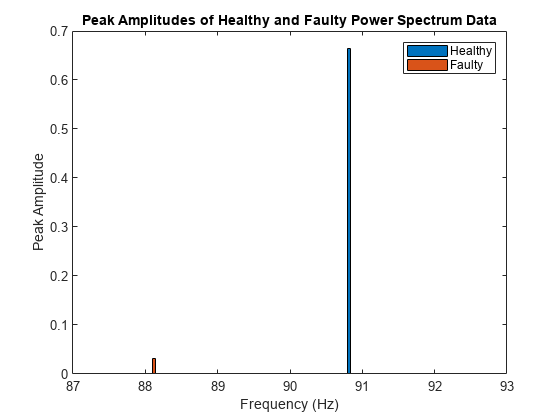
PeakFrequencies = spectralMetrics_total(:,2:3:end-1).Variables';
PeakAmplitudes = spectralMetrics_total(:,1:3:end-1).Variables';
bar(PeakFrequencies, PeakAmplitudes);
legend('Healthy','Faulty')
xlabel('Frequency (Hz)')
ylabel('Peak Amplitude')
title('Peak Amplitudes of Healthy and Faulty Power Spectrum Data') 

ズームインして、最初の回転シャフトの 1 番目の高調波におけるピーク振幅の変化を確認します。

xlim([87 93])
ylim([0 0.7])

[スペクトル特徴の抽出] ライブ エディター タスクの使用

この例で示したように、[スペクトル特徴の抽出] ライブ エディター タスクはいくつかの異なった用途で有用であることがわかります。ライブ エディター タスクを使うと、スペクトルのピークを既知のマシン コンポーネントの周波数と簡単にマッチングできます。これは、データと、データのさまざまな特徴を発生させている機械コンポーネントをより良く理解するために役立ちます。

[スペクトル特徴の抽出] ライブ エディター タスクのもう 1 つの用途は、対象とする周波数範囲でスペクトル データを特徴付けるメトリクスを生成することです。タスクでは、各故障周波数帯域のピーク振幅、ピーク周波数、および帯域パワーと、すべての故障周波数帯域の合計帯域パワーを含む、出力 table が生成されます。ただし、これらはタスクで入力したパワー スペクトル データに固有なメトリクスです。

この用法を拡張して、新規データ セットを収集しながら経時的にメトリクスを追跡できるようにするには、タスク内でパワー スペクトル データを更新するか、あるいは自動生成された MATLAB コードを使用してメトリクス テーブルを生成することができます。生成された MATLAB コードをコピーするのは、多くの新しいデータ セットについて故障帯域のメトリクスを継続的に計算するための簡単な方法です。

タスクの 3 つ目の用法は、上記 2 つの用法の利点を組み合わせたものです。タスクではさまざまな機械コンポーネントがスペクトル データのピークと関連付けられるため、どのコンポーネントがスペクトル データの大きな変化の原因となっているかを、つまり潜在的な故障をすばやく特定することができます。たとえば、スペクトル データから導出される機械故障の一般的なインジケーターとして、スペクトル ピークの振幅における変化があります。スペクトル メトリクスの table で、ピーク振幅または帯域パワーが時間とともに大きく低下するのに気付いた場合、対応するピーク周波数をプロットに戻って追跡し、どのコンポーネントの故障周波数帯域がそのピークと合致しているかを確認できます。

参考

faultBands | bearingFaultBands | gearMeshFaultBands | faultBandMetrics | スペクトル特徴の抽出

関連するトピック

• ライブ スクリプトへの対話型タスクの追加