リアプノフ指数の推定
等間隔にサンプリングされた信号のリアプノフ指数をライブ エディターで対話的に推定
説明
[リアプノフ指数の推定] タスクでは、等間隔にサンプリングされた信号のリアプノフ指数を対話的に推定できます。このタスクは、ライブ スクリプト用の MATLAB® コードを自動生成します。ライブ エディター タスク全般の詳細については、ライブ スクリプトへの対話型タスクの追加を参照してください。
リアプノフ指数を使用して、位相空間での限りなく近い軌跡の分離率を特徴付け、異なるアトラクターを区別します。リアプノフ指数は、システムにおける無秩序性のレベルの定量化に役立ち、潜在的な故障の検出に使用できます。負のリアプノフ指数は収束を示し、正のリアプノフ指数は発散や無秩序性を示します。
タスクを開く
MATLAB エディターでライブ スクリプトに [リアプノフ指数の推定] タスクを追加するには、次を行います。
[ライブ エディター] タブで、[タスク] 、 [リアプノフ指数の推定] を選択します。
スクリプトのコード ブロック内で、「
Lyapunov」や「Lyapunov exponent」などの関連するキーワードを入力します。コマンドの補完候補から[リアプノフ指数の推定]を選択します。
例
ライブ エディターで [リアプノフ指数の推定] タスクを使用して、等間隔にサンプリングされた信号のリアプノフ指数を対話的に推定します。ラグ、埋め込み次元、拡大範囲、平均周期のさまざまな値を試して、線形近似の線を元のデータのプロットに合わせます。このタスクでは、自分が選択した内容を反映するコードが自動的に生成されます。
この例では、100 Hz でサンプリングして再構成された位相空間信号 phaseSpace を含む 'lyapExpData.mat' について考えます。
load('lyapExpData.mat','phaseSpace')
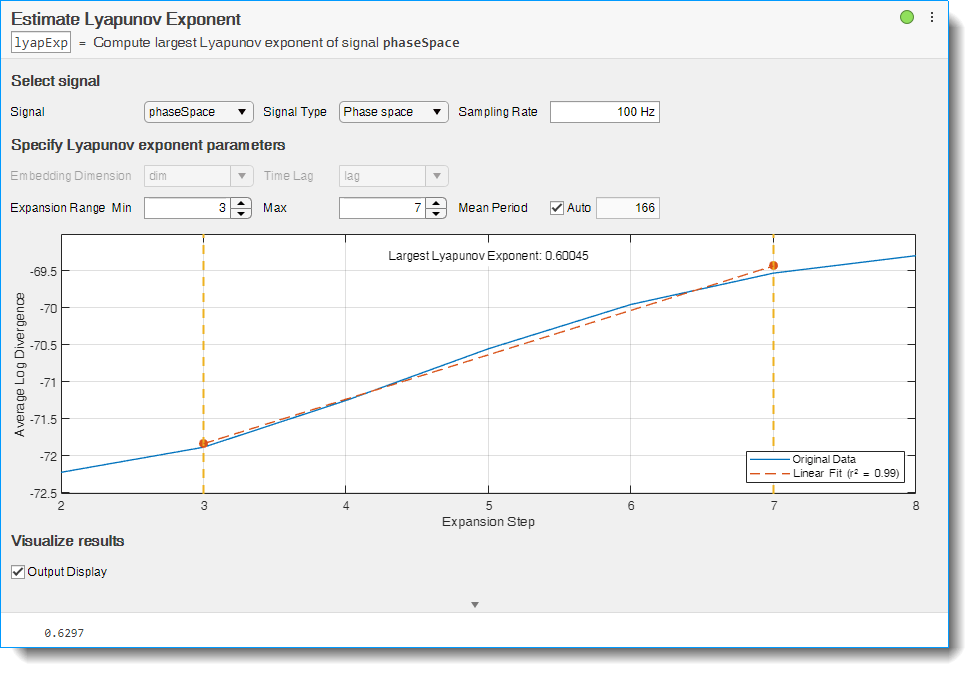
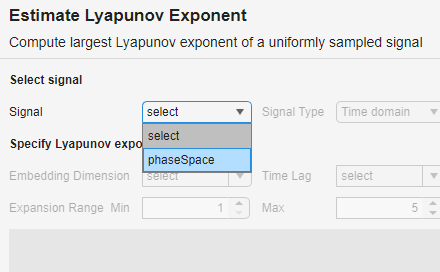
信号 phaseSpace のリアプノフ指数を推定するには、ライブ エディターで [リアプノフ指数の推定] タスクを開きます。[ライブ エディター] タブで、[タスク]、[リアプノフ指数の推定] を選択します。タスクで信号 phaseSpace を選択します。
選択した信号は位相空間信号であるため、[信号タイプ] メニューから Phase space を選択します。信号は 100 Hz でサンプリングされているため、この値を [サンプリング レート] フィールドで指定します。
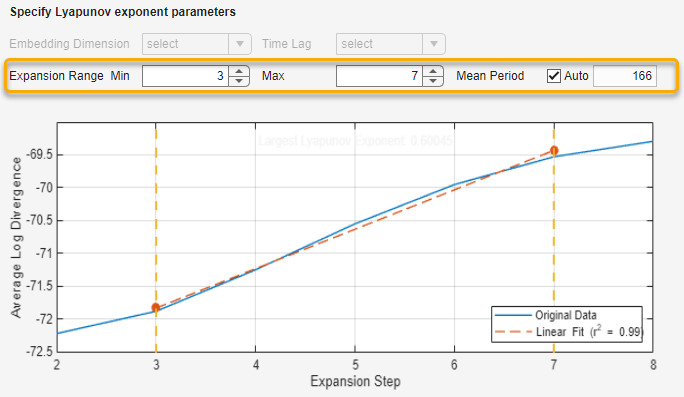
[リアプノフ指数の推定] タスクにより、埋め込み次元とラグが位相空間データから自動的に計算され、拡大範囲と平均周期には既定値を使用してリアプノフ指数のプロットが作成されます。
線形近似の線が既定の拡大範囲の値を使用すると元のデータの線と揃わない場合は、十分に揃うまで [拡大範囲] の [最小値]、[拡大範囲] の [最大値]、および [平均周期] のフィールドの値を変えて試します。この例では、最小値 3 と最大値 7 を使用すると最も揃った状態になります。平均周期については、信号 phaseSpace は既定値の 166 で適切に揃います。
ライブ エディターの出力にリアプノフ指数の値の出力を表示するかどうかは、[出力表示] オプションを使用して切り替えることができます。
このタスクは、ライブ スクリプトにコードを生成します。生成されたコードには、指定したパラメーターとオプションが反映されます。生成されたコードを確認するには、タスク パラメーター エリアの下部にある 
をクリックします。タスクが展開されて、生成されたコードが表示されます。
既定では、生成されたコードは出力変数の名前として lyapExp を使用します。別の出力変数名を指定するには、タスクの一番上にあるサマリー行に新しい名前を入力します。たとえば、名前を lExponent に変更します。
タスクによって、生成されたコードが更新されて新しい変数名が反映され、新しい変数 lExponent が MATLAB ワークスペースに表示されます。負のリアプノフ指数は収束を示し、正のリアプノフ指数は発散や無秩序性を示します。lExponent の振幅は、限りなく近い軌跡の収束または発散の速度を示す指標です。
関連する例
パラメーター
バージョン履歴
R2019b で導入
