このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

approximateEntropy

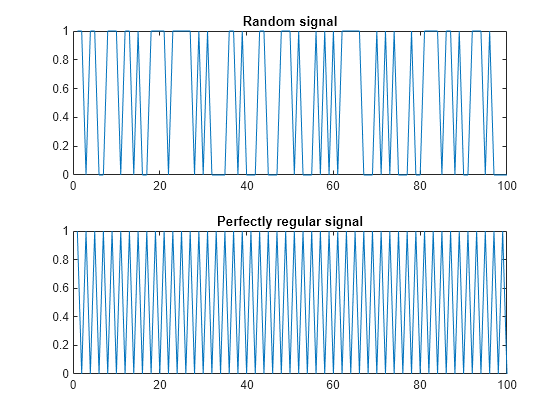
非線形時系列の規則性の測定

構文

approxEnt = approximateEntropy(X)

approxEnt = approximateEntropy(X,lag)

approxEnt = approximateEntropy(X,[],dim)

approxEnt = approximateEntropy(X,lag,dim)

approxEnt = approximateEntropy(___,Name,Value)

説明

approxEnt = approximateEntropy(X) は、位相空間を再構成することにより、等間隔にサンプリングされた時間領域信号 X の近似エントロピーを推定します。近似エントロピーは、時系列上の変動の規則性と予測不可能性を定量化する尺度です。

approxEnt = approximateEntropy(X,lag) は、時間遅延 lag に対する近似エントロピーを推定します。

approxEnt = approximateEntropy(X,[],dim) は、埋め込み次元 dim に対する近似エントロピーを推定します。

approxEnt = approximateEntropy(X,lag,dim) は、時間遅延 lag と埋め込み次元 dim に対する近似エントロピーを推定します。

approxEnt = approximateEntropy(___,Name,Value) は、1 つ以上の Name,Value ペア引数で指定された追加オプションを使用して、近似エントロピーを推定します。

例

信号の近似エントロピーの計算

この例では、比較のために 2 つの信号を生成します $-$ 乱数信号 xRand と、完全に規則的な信号 xReg です。乱数信号の再現性を高めるために rng を default に設定します。

rng('default');
xRand = double(randn(100,1)>0);
xReg = repmat([1;0],50,1);

乱数信号と規則的な信号を可視化します。

figure;
subplot(2,1,1);
plot(xRand);
title('Random signal');
subplot(2,1,2);
plot(xReg);
title('Perfectly regular signal');

このプロットから、規則的な信号の方が乱数信号よりも予測しやすいことがわかります。

2 つの信号の近似エントロピーを求めてみましょう。

valueReg = approximateEntropy(xReg)

valueReg = 5.1016e-05

valueIrreg = approximateEntropy(xRand)

valueIrreg = 0.6849

完全に規則的な信号の近似エントロピーは、乱数信号よりも著しく小さくなります。したがって、多くの反復パターンを含む完全に規則的な信号の近似エントロピーの値は比較的小さく、予測性の低い乱数信号の近似エントロピーの値は大きくなります。

データの近似エントロピーの計算

この例では、円形の軌跡をたどるクワッドコプターの位置データを考えてみましょう。ファイル uavPositionData.mat には、コプターが移動した x、y、z 方向の位置データが含まれています。

データ セットを読み込み、クワッドコプターの軌跡を 3 次元で可視化します。

load('uavPositionData.mat','xv','yv','zv');
plot3(xv,yv,zv);

この例では、x 方向の位置データのみを計算に使用します。Lag は不明であるため、phaseSpaceReconstruction を用いて遅延を推定します。'Dimension' を 3 に設定します。Dimension パラメーターと Lag パラメーターは、データの近似エントロピーを計算するために必要です。

dim = 3;
[~,lag] = phaseSpaceReconstruction(xv,[],dim)

lag = 4

前のステップで得られた Lag の値を用いて、近似エントロピーを求めます。

approxEnt = approximateEntropy(xv,lag,dim)

approxEnt = 0.1088

クワッドコプターはあらかじめ定義された半径の円形軌跡を移動するため、位置データは規則的です。したがって近似エントロピーの値は低くなります。

入力引数

X — 等間隔にサンプリングされた時間領域信号

ベクトル | 配列 | timetable

等間隔にサンプリングされた時間領域信号。ベクトル、配列、timetable のいずれかで指定します。X が複数列の場合、approximateEntropy は X を多変量信号として扱い、近似エントロピーを計算します。

X が行ベクトルとして指定された場合、approximateEntropy はこれを一変量信号として扱います。

dim — 埋め込み次元

スカラー | ベクトル

埋め込み次元。スカラーまたはベクトルとして指定します。dim は 'Dimension' の名前と値のペアと等価です。

lag — 時間遅延

スカラー | ベクトル

時間遅延。スカラーまたはベクトルとして指定します。lag は'Lag' の名前と値のペアと等価です。

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペア自体は順不同で構いません。

R2021a 以前は、名前と値をそれぞれコンマで区切り、 Name を引用符で囲みます。

例: ...,'Dimension',3

Dimension — 埋め込み次元

2 (既定値) | スカラー | ベクトル

埋め込み次元。'Dimension' とスカラーまたはベクトルで構成されるコンマ区切りのペアとして指定します。Dimension がスカラーである場合は、X の各列は、Dimension を使用して再構成されます。X の列数と同じ長さのベクトルを Dimension としたとき、列 i の再構成次元は Dimension(i) になります。

システムの次元に基づいて Dimension を指定します。埋め込み次元の詳細については、phaseSpaceReconstruction を参照してください。

Lag — 位相空間の再構成の遅延

1 (既定値) | スカラー | ベクトル

位相空間の再構成の遅延。'Lag' とスカラーで構成されるコンマ区切りのペアとして指定します。Lag がスカラーである場合は、X の各列は、Lag を使用して再構成されます。X の列数と同じ長さのベクトルを Lag としたとき、列 i の再構成の遅延は Lag(i) になります。

遅延が小さすぎると、データにランダム ノイズが入ります。一方、ラグが大きすぎると、再構成されたダイナミクスは時系列の真のダイナミクスを表しません。最適な遅延の計算の詳細については、phaseSpaceReconstruction を参照してください。

Radius — 類似性の基準

0.2*std(X) | 0.2*sqrt(trace(cov(X))) | スカラー

類似性の基準。'Radius' とスカラーで構成されるコンマ区切りのペアとして指定します。類似性の基準は、類似性の半径とも呼ばれ、データの変動が類似であると考えられる有意な範囲を特定するために使用される、調整パラメーターです。

Radius の既定値は以下のとおりです。

• X が 1 列の場合は、0.2*std(X)。

• X が複数列の場合は、0.2*sqrt(trace(cov(X)))。

出力引数

approxEnt — 非線形時系列の近似エントロピー

スカラー

非線形時系列の近似エントロピー。スカラーとして返されます。近似エントロピーは、時系列における変動の予測不可能性を定量化する規則性の統計量です。近似エントロピーの値が比較的高い場合は、観測の類似したパターンに、さらに類似した観測が続かない可能性を反映しています。

たとえば、2 つのバイナリ信号 S1 と S2 を考えてみましょう。

S1 = [0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1];

S2 = [1 1 0 1 1 1 1 0 1 0 1 0 0 0 0 1];

信号 S1 は、0 と 1 を交互に繰り返すため、完全に規則的です。つまり、前の値がわかっていれば、次の値を予測できます。しかし、信号 S2 は、前の値が前もってわかっていても、次の値を把握できません。したがって、信号 S2 は乱数信号であり、予測可能性は低いといえます。したがって、反復性の高いパターンを含む信号は approxEnt の値が相対的に小さく、予測性の低い信号は approxEnt の値が相対的に大きくなります。

規則性の尺度として approximateEntropy を使用し、時系列内の複雑度を定量化します。データ セット内の複雑度を識別する機能は、工学分野では部品の振動や音響信号を調べて故障を推定するうえで役立ちます。臨床分野では、たとえば脳波 (EEG) のパターンを観察して発作の発生確率を予測するうえで役立ちます。[2][3]

アルゴリズム

近似エントロピーは、以下の方法で計算されます。

1. まず、関数 approximateEntropy が、埋め込み次元 m とラグ τ を持つ N 個のデータ点に対して、遅延した再構成 Y_1:N を生成します。

2. 次に、点 i において、次の式で範囲内の点の数を計算します。

   $$N_i={\displaystyle \sum _{i=1,i\ne k}^{N}1\left({\Vert Y_i-Y_k\Vert }_{\infty }<R\right)}$$

   ここで、1 は指示関数、R は類似性の半径です。

3. 次に、近似エントロピーが $$approxEnt={\Phi }_m-{\Phi }_{m+1}$$ として計算されます。ここで、

   $${\Phi }_m={\left(N-m+1\right)}^{-1}{\displaystyle \sum _{i=1}^{N-m+1}\log \left(N_i\right)}$$

参照

[1] Pincus, Steven M. "Approximate entropy as a measure of system complexity." Proceedings of the National Academy of Sciences. 1991 88 (6) 2297-2301; doi:10.1073/pnas.88.6.2297.

[2] U. Rajendra Acharya, Filippo Molinari, S. Vinitha Sree, Subhagata Chattopadhyay, Kwan-Hoong Ng, Jasjit S. Suri. "Automated diagnosis of epileptic EEG using entropies." Biomedical Signal Processing and Control Volume 7, Issue 4, 2012, Pages 401-408, ISSN 1746-8094.

[3] Caesarendra, Wahyu & Kosasih, P & Tieu, Kiet & Moodie, Craig. "An application of nonlinear feature extraction-A case study for low speed slewing bearing condition monitoring and prognosis." IEEE/ASME International Conference on Advanced Intelligent Mechatronics: Mechatronics for Human Wellbeing, AIM 2013.1713-1718. 10.1109/AIM.2013.6584344.

[4] Kantz, H., and Schreiber, T. Nonlinear Time Series Analysis. Cambridge: Cambridge University Press, 2003.

拡張機能

C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。

バージョン履歴

R2018a で導入

参考

correlationDimension | phaseSpaceReconstruction | lyapunovExponent