このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

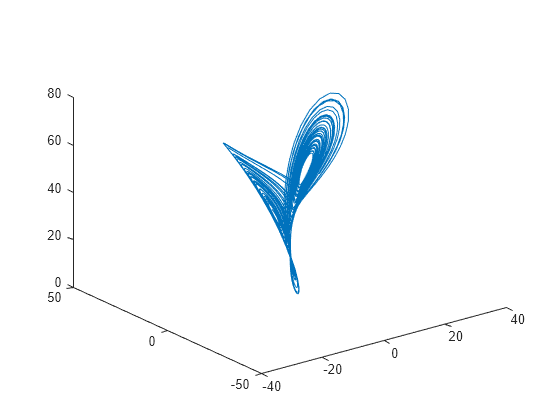
correlationDimension

無秩序な信号の複雑度の測定

構文

corDim = correlationDimension(X)

corDim = correlationDimension(X,lag)

corDim = correlationDimension(X,[],dim)

corDim = correlationDimension(X,lag,dim)

[corDim,rRange,corInt] = correlationDimension(___)

___ = correlationDimension(___,Name,Value)

correlationDimension(___)

説明

corDim = correlationDimension(X) は、等間隔にサンプリングされた時間領域信号 X の相関次元を推定します。相関次元は、一連の乱数点が占める空間の次元の尺度です。corDim は、相関積分対類似性の半径の範囲の勾配として推定されます。correlationDimension を特徴的な尺度として使用して、確定的な無秩序性とランダム ノイズを区別し、潜在的な故障を検出します。[1]

corDim = correlationDimension(X,lag) は、時間遅延 lag の等間隔にサンプリングされた時間領域信号 X の相関次元を推定します。

corDim = correlationDimension(X,[],dim) は、埋め込み次元 dim の等間隔にサンプリングされた時間領域信号 X の相関次元を推定します。

corDim = correlationDimension(X,lag,dim) は、時間遅延 lag と埋め込み次元 dim の等間隔にサンプリングされた時間領域信号 X の相関次元を推定します。

また、[corDim,rRange,corInt] = correlationDimension(___) は、等間隔にサンプリングされた時間領域信号 X の類似性の半径の範囲と相関積分を推定します。相関積分は、システムの状態が 2 つの異なる時間間隔において近い可能性の平均であり、自己相似性を反映しています。

___ = correlationDimension(___,Name,Value) は、1 つ以上の Name,Value ペア引数で指定された追加オプションを使用して、相関次元を推定します。

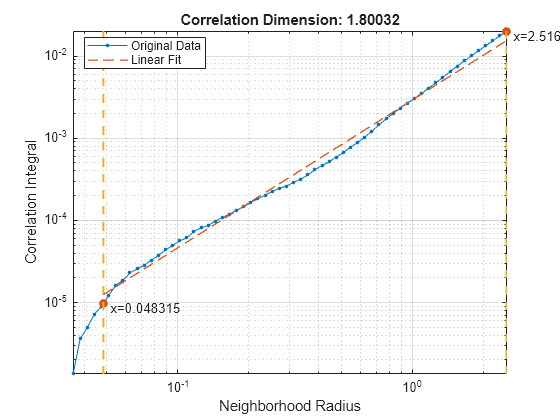
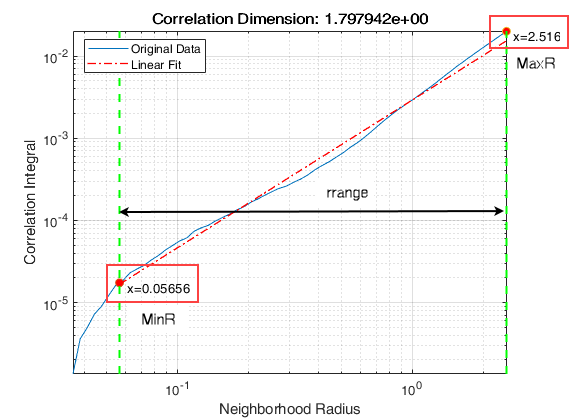
出力引数のない correlationDimension(___) は、相関積分対近傍半径のプロットを作成します。

例

データの相関次元の推定と可視化

この例では、無秩序解の一意のセットを記述するローレンツ アトラクターについて検討します。

データ セットを読み込み、ローレンツ アトラクターを 3D で可視化します。

load('lorenzAttractorExampleData.mat','data');
plot3(data(:,1),data(:,2),data(:,3));

この例では、ローレンツ アトラクターの x 方向のデータのみを使用します。lag は不明であるため、phaseSpaceReconstruction を用いて遅延を推定します。ローレンツ アトラクターは 3 次元系であるため、'Dimension' を 3 に設定します。dim パラメーターと lag パラメーターは、相関積分対近傍半径のプロットを作成するために必要です。

xdata = data(:,1);
dim = 3;
[~,lag] = phaseSpaceReconstruction(xdata,[],dim)

lag = 10

前のステップで得られた lag の値を用いて、ローレンツ アトラクターの相関積分対近傍半径のプロットを作成します。'NumPoints' に適切な値を設定して、近傍半径の適切な解像度を決定します。

Np = 100;
correlationDimension(xdata,lag,dim,'NumPoints',Np);

1 本目の緑の垂直破線 (左側) は、MinRadius の値を示し、2 本目の緑の垂直破線 (右側) は、MaxRadius を示しています。赤の破線は、計算された半径の範囲内で、相関積分対近傍半径のデータに対する線形近似線を示しています。

相関次元を計算するには、まず、正確な推定に必要な MinRadius と MaxRadius の値を決定する必要があります。

プロットで 2 本の緑の垂直破線をドラッグして、元のデータ線に線形近似線を "最適適合" させ、半径の範囲を求めます。

2 本の垂直線をドラッグして適切に適合させた後の、MinRadius と MaxRadius の新しい値を確認します。

前のステップで得られた新しい MinRadius と MaxRadius の値を用いて、ローレンツ アトラクターの相関次元を求めます。

MinR = 0.05656;
MaxR = 2.516;
corDim = correlationDimension(xdata,[],dim,'MinRadius',MinR,'MaxRadius',MaxR,'NumPoints',Np)

corDim = 1.7490

相関次元の値は、システム内の無秩序性のレベルに正比例します。つまり、corDim の値が高いほど、システム内の無秩序な複雑度が高いことを表します。

入力引数

X — 等間隔にサンプリングされた時間領域信号

ベクトル | 配列 | timetable

等間隔にサンプリングされた時間領域信号。ベクトル、配列、timetable のいずれかで指定します。X が複数列の場合、correlationDimension は X を多変量信号として扱い、相関次元を計算します。

X が行ベクトルとして指定された場合、correlationDimension はこれを一変量信号として扱います。

dim — 埋め込み次元

スカラー | ベクトル

埋め込み次元。スカラーまたはベクトルとして指定します。dim は 'Dimension' の名前と値のペアと等価です。

lag — 時間遅延

スカラー | ベクトル

時間遅延。スカラーまたはベクトルとして指定します。lag は'Lag' の名前と値のペアと等価です。

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペア自体は順不同で構いません。

R2021a 以前は、名前と値をそれぞれコンマで区切り、 Name を引用符で囲みます。

例: ...,'Dimension',3

Dimension — 埋め込み次元

2 (既定値) | スカラー | ベクトル

埋め込み次元。'Dimension' とスカラーまたはベクトルで構成されるコンマ区切りのペアとして指定します。Dimension がスカラーである場合は、X の各列は、Dimension を使用して再構成されます。X の列数と同じ長さのベクトルを Dimension としたとき、列 i の再構成次元は Dimension(i) になります。

システムの次元、つまり状態数に基づいて Dimension を指定します。埋め込み次元の詳細については、phaseSpaceReconstruction を参照してください。

Lag — 位相空間の再構成の遅延

1 (既定値) | スカラー | ベクトル

位相空間の再構成の遅延。'Lag' とスカラーまたはベクトルのいずれかで構成されるコンマ区切りのペアで指定します。Lag がスカラーである場合は、X の各列は、Lag を使用して再構成されます。X の列数と同じ長さのベクトルを Lag としたとき、列 i の再構成の遅延は Lag(i) になります。

遅延が小さすぎると、データにランダム ノイズが入ります。一方、ラグが大きすぎると、再構成されたダイナミクスは時系列の真のダイナミクスを表しません。最適な遅延の推定の詳細については、phaseSpaceReconstruction を参照してください。

MinRadius — 類似性の最小半径

MaxRadius/1000 (既定値) | スカラー

類似性の最小半径。'MinRadius' とスカラーで構成されるコンマ区切りのペアとして指定します。相関次元プロットの線形近似を調整して、MinRadius の最適値を求めます。

MaxRadius — 類似性の最大半径

0.2*sqrt(trace(cov(X))) (既定値) | スカラー

類似性の最大半径。'MaxRadius' とスカラーで構成されるコンマ区切りのペアとして指定します。相関次元プロットの線形近似を調整して、MaxRadius の最適値を求めます。

NumPoints — 計算の点の数

10 (既定値) | 正のスカラー整数

計算の点の数。'NumPoints' と正のスカラー整数で構成されるコンマ区切りのペアとして指定します。NumPoints は、MinRadius と MaxRadius の間にある点の数です。rRange に必要な分解能に基づき、NumPoints の適切な値を選択します。

NumPoints は 1 より大きい値のみを受け入れ、既定値は 10 です。

出力引数

corDim — 相関次元

スカラー

相関次元。スカラーとして返されます。corDim は、多次元位相空間における無秩序な信号の複雑度の尺度であり、相関積分対類似性の半径の範囲の勾配です。corDim は、確定的な無秩序性とランダム ノイズを区別する特徴的な尺度として、故障検出に使用されます。

rRange — 類似性の半径の範囲

配列

類似性の半径。配列として返されます。rRange は、NumPoints で定義される同数の点に分割された MaxRadius と MinRadius の差です。

corInt — 相関積分

配列

相関積分。配列として返されます。corInt は、2 つの異なる時点での状態が近い可能性の平均であり、自己相似性を反映しています。NumPoints は配列 corInt の長さを定義します。

アルゴリズム

相関次元は、以下の方法で計算されます。

1. まず、関数 correlationDimension が、埋め込み次元 m とラグ τ をもつ、遅延した再構成 Y_1:N を生成します。

2. 次に、点 i において、次の式で範囲内の点の数を計算します。

   $$N_i\left(R\right)={\displaystyle \sum _{i=1,i\ne k}^{N}1\left(\Vert Y_i-Y_k\Vert <R\right)}$$

   ここで、1 は指示関数、R は、R = exp(linspace(log(r_min), log(r_max), N)). で与えられる類似性の半径です。ここで、r_min は MinRadius、r_max は MaxRadius、N は NumPoints です。

3. 相関次元 corDim は、C(R) vs. R の勾配です。ここで、相関積分 C(R) は、

   $$C\left(R\right)=\frac{2}{N\left(N-1\right)}{\displaystyle \sum _{i=1}^N{N}_i\left(R\right)}$$

   として定義されます。

参照

[1] Caesarendra, Wahyu & Kosasih, P & Tieu, Kiet & Moodie, Craig. "An application of nonlinear feature extraction-A case study for low speed slewing bearing condition monitoring and prognosis." IEEE/ASME International Conference on Advanced Intelligent Mechatronics: Mechatronics for Human Wellbeing, AIM 2013.1713-1718. 10.1109/AIM.2013.6584344.

[2] Theiler, James. "Efficient algorithm for estimating the correlation dimension from a set of discrete points". American Physical Society. Physical Review A 1987/11/1. Volume 36. Issue 9. Pages 44-56.

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用に関するメモと制限:

• プロットを生成する構文は、コード生成ではサポートされません。

バージョン履歴

R2018a で導入

参考

approximateEntropy | phaseSpaceReconstruction | lyapunovExponent