このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

phaseSpaceReconstruction

観測された時系列の状態ベクトルへの変換

構文

XR = phaseSpaceReconstruction(X,lag,dim)

[XR,eLag,eDim] = phaseSpaceReconstruction(X)

[XR,eLag,eDim] = phaseSpaceReconstruction(X,lag)

[XR,eLag,eDim] = phaseSpaceReconstruction(X,[],dim)

[___] = phaseSpaceReconstruction(___,Name,Value)

phaseSpaceReconstruction(___)

説明

XR = phaseSpaceReconstruction(X,lag,dim) は、時間遅延 lag と埋め込み次元 dim を入力として、等間隔にサンプリングされた時間領域信号 X の再構成された位相空間 XR を返します。

phaseSpaceReconstruction を使用してシステム次数を検証し、システムのプロパティを維持したまま、すべての動的システム変数を再構成します。位相空間の再構成は、利用できるデータが限られている場合や、位相空間の次元やラグが不明な場合に有効です。非線形特徴量 approximateEntropy、correlationDimension、lyapunovExponent は、計算の最初の手順として phaseSpaceReconstruction を使用します。

[XR,eLag,eDim] = phaseSpaceReconstruction(X) は、推定された遅延 eLag と埋め込み次元 eDim とともに、再構成された位相空間 XR を返します。

[XR,eLag,eDim] = phaseSpaceReconstruction(X,lag) は、lag. によって指定された時間遅延を使用して、等間隔にサンプリングされた時間領域信号 X の再構成された位相空間 XR と埋め込み次元 eDim を返します。

[XR,eLag,eDim] = phaseSpaceReconstruction(X,[],dim) は、dim によって指定された埋め込み次元を使用して、等間隔にサンプリングされた時間領域信号 X の再構成された位相空間 XR と時間遅延 eLag を返します。

[___] = phaseSpaceReconstruction(___,Name,Value) は、1 つ以上の Name,Value ペア引数で指定された追加オプションを使用して、再構成された位相空間 XR を返します。

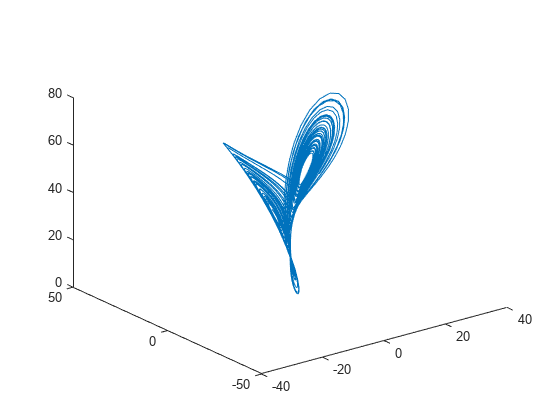
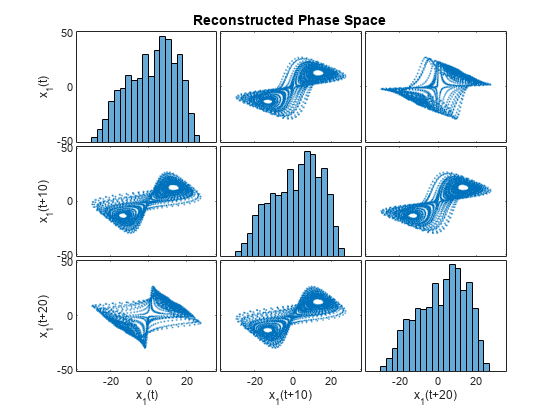
出力引数のない phaseSpaceReconstruction(___) は、対角に沿ったヒストグラム プロットとともに、再構成された位相空間のサブ座標軸の行列を作成します。

例

位相空間の再構成を使用したデータの再構成

この例では、ローレンツ アトラクターの測定値を持っているものとします。測定値は x 方向のみですが、アトラクターは 3 次元系です。この限られたデータを使用して、元のシステムのプロパティを保持するように位相空間を再構成します。

ローレンツ アトラクター データを読み込み、その x、y、z 測定値を 3 次元プロットに可視化します。

load('lorenzAttractorExampleData.mat','data');
plot3(data(:,1),data(:,2),data(:,3));

x 方向の測定値を使用してラグと次元を推定します。

xdata = data(:,1);
[~,eLag,eDim] = phaseSpaceReconstruction(xdata)

eLag = 10

eDim = 3

ローレンツ アトラクターは 3 次元データを持っているため、推定された埋め込み次元 eDim は 3 です。

推定されたラグと埋め込み次元とともに、再構成された位相空間を可視化します。

phaseSpaceReconstruction(xdata,eLag,eDim);

3 行 3 列の位相空間プロットからわかるように、アトラクターのトポロジーが回復しています。${\mathit{x}}_1\left(\mathit{t}+10\right)$ および ${\mathit{x}}_1\left(\mathit{t}+20\right)$ は、推定されたラグの値 10 で再構成された他の 2 つの状態です。対角プロット (1,1)、(2,2)、(3,3) は、それぞれ ${\mathit{x}}_1\left(\mathit{t}\right)$、${\mathit{x}}_1\left(\mathit{t}+10\right)$、${\mathit{x}}_1\left(\mathit{t}+20\right)$ データのヒストグラムを表しています。

入力引数

X — 等間隔にサンプリングされた時間領域信号

ベクトル | 配列 | timetable

等間隔にサンプリングされた時間領域信号。ベクトル、配列、timetable のいずれかで指定します。X に複数の列が存在する場合は、各列は独立した時系列として扱われます。

X が行ベクトルとして指定された場合、phaseSpaceReconstruction はこれを一変量信号として扱います。

dim — 埋め込み次元

スカラー | ベクトル

埋め込み次元。スカラーまたはベクトルとして指定します。dim は、測定から始まる位相図を再構成する空間の次元です。

dim がスカラーである場合は、X の各列は、dim を使用して再構成されます。X の列数と同じ長さのベクトルを dim としたとき、列 i の再構成次元は dim(i) になります。

lag — 位相空間の再構成で使用される遅延の値

スカラー | ベクトル

位相空間の再構成で使用される遅延の値。スカラーまたはベクトルとして指定します。lag がスカラーである場合は、X の各列は、lag を使用して再構成されます。X の列数と同じ長さのベクトルを lag としたとき、列 i の再構成の遅延は lag(i) になります。

時間遅延が小さすぎると、状態にランダム ノイズが入ります。一方、ラグが大きすぎると、再構成されたダイナミクスは時系列の真のダイナミクスを表しません。

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペア自体は順不同で構いません。

R2021a 以前は、名前と値をそれぞれコンマで区切り、 Name を引用符で囲みます。

例: …'HistogramBins',12

HistogramBins — 離散化用ビン数

10 (既定値) | スカラー

離散化用ビン数。'HistogramBins' とスカラーで構成されるコンマ区切りのペアとして指定します。HistogramBins は、遅延 eLag を推定するために平均相互情報量 (AMI) を計算する必要があります。

X の長さを基準に HistogramBins の値を設定します。

MaxLag — ラグの最大値

10 (既定値) | スカラー

ラグの最大値。'MaxLag' とスカラーで構成されるコンマ区切りのペアとして指定します。MaxLag は、平均相互情報量 (AMI) アルゴリズムを使用して遅延 est_delay を推定するために使用されます。

PercentFalseNeighbors — 埋め込み次元を決定する係数

0.1 (既定値) | スカラー

埋め込み次元を決定する係数。'PercentFalseNeighbors' とスカラーで構成されるコンマ区切りのペアとして指定します。ある次元 d において、偽最近傍の割合が調整パラメーター PercentFalseNeighbors を下回ると、d が埋め込み次元と見なされます。

PercentFalseNeighbors の既定値は 0.1 であり、許容可能な値は 0 ～ 1 の範囲内にあります。

DistanceThreshold — 偽近傍と判定するための距離しきい値

10 (既定値) | スカラー

偽近傍と判定するための距離しきい値。'DistanceThreshold' とスカラーで構成されるコンマ区切りのペアとして指定します。DistanceThreshold は、再構成された位相空間において、偽最近傍となる点の数を決定するための調整パラメーターです。

DistanceThreshold の既定値は 10 であり、推奨値は 10 ～ 50 の範囲内にあります。

MaxDim — 埋め込み次元の最大値

5 (既定値) | スカラー

埋め込み次元の最大値。'MaxDim' とスカラーで構成されるコンマ区切りのペアとして指定します。

システムの状態数が 5 を超える場合は、MaxDim の値を変更します。

出力引数

XR — 再構成された位相空間

配列 | timetable

再構成された位相空間。配列または timetable として返されます。XR には、埋め込み次元とラグの値に基づいた状態ベクトルが含まれます。

eLag — 推定された時間遅延

スカラー

推定された時間遅延。X のサイズに関係なく、スカラーとして返されます。

eLag は、平均相互情報量 (AMI) アルゴリズムを使用して推定されます。詳細については、アルゴリズムを参照してください。

eDim — 推定された埋め込み次元

スカラー

推定された埋め込み次元。X のサイズに関係なく、スカラーとして返されます。

eDim は、偽最近傍 (FNN) アルゴリズムを使用して推定されます。詳細については、アルゴリズムを参照してください。

アルゴリズム

位相空間の再構成

等間隔にサンプリングされた一変量時間信号 $$X_1={\left(x_{1,1},x_{1,2},\mathrm{...},x_{1,N}\right)}^T$$ に対して、phaseSpaceReconstruction は、遅延した再構成

$$X_{1,i}^r=\left(x_{1,i},x_{1,i+{\tau }_1},\mathrm{...},x_{1,i+\left(m_1-1\right){\tau }_1}\right),i=1,2,\mathrm{...},N-\left(m_1-1\right){\tau }_1$$

を計算します。ここで、N は時系列の長さ、τ₁ はラグ、m₁ は X₁ の埋め込み次元です。

同様に、多変量時系列 X が与えられた場合は、

$$X=\left[X_1,X_2,\mathrm{...},X_S\right]=\left[\begin{array}{cc}\begin{array}{cc}\begin{array}{l}{x}_{1,1}\\ ⋮\\ x_{1,N}\end{array}& \begin{array}{l}\dots \\ \ddots \\ \cdots \end{array}\end{array}& \begin{array}{l}{x}_{S,1}\\ ⋮\\ x_{S,N}\end{array}\end{array}\right]$$

phaseSpaceReconstruction は各時系列に対して、以下のように再構成を計算します。

$$X_i^r=\left(X_{1,i}^r,X_{2,i}^r,\mathrm{...},X_{S,i}^r\right),i=1,2,\mathrm{...},N-\left(\max \left\{m_i\right\}-1\right)\left(\max \left\{{\tau }_i\right\}\right)$$

ここで、S は測定値の数、N は時系列の長さです。

遅延の推定

位相空間の再構成の遅延は、平均相互情報量 (AMI) アルゴリズムを使用して推定されます。再構成の場合は、時間遅延は AMI の最初の局所的最小値となるように設定されます。

平均相互情報量は、以下のように計算されます。

$$AMI\left(T\right)={\displaystyle \sum _{i=1}^{N}p\left(x_i,x_{i+T}\right){\log }_2\left[\frac{p\left(x_i,x_{i+T}\right)}{p\left(x_i\right)p\left(x_{i+T}\right)}\right]}$$

ここで、N は、時系列の長さであり、Τ = 1:MaxLag です。

埋め込み次元の推定

位相空間の再構成の埋め込み次元は、偽最近傍 (FNN) アルゴリズムを使用して推定されます。

• 次元 d の点 i に対して、再構成された位相空間 {X^r_i}, i = 1:N の点 X^r_i とその最近接点 X^r*_i は、以下の場合に偽近傍です。

  $$\sqrt{\frac{R_i^2\left(d+1\right)-R_i^2\left(d\right)}{R_i^2\left(d\right)}}>DistanceThreshold$$

  ここで、$$R_i^2\left(d\right)={\Vert X_i^r-X_i^{r*}\Vert }^2$$ は距離計量です。

• 推定された埋め込み次元 d は、条件 p_fnn < PercentFalseNeighbors を満たす最小値であり、ここで、p_fnn は再構成された位相空間の点の合計数に対する FNN 点の比率を表します。

参照

[1] Rhodes, Carl & Morari, Manfred. "False Nearest Neighbors Algorithm and Noise Corrupted Time Series." Physical Review. E. 55.10.1103/PhysRevE.55.6162.

[2] Kliková, B., and Aleš Raidl. "Reconstruction of phase space of dynamical systems using method of time delay." Proceedings of the 20th Annual Conference of Doctoral Students WDS 2011.

[3] I. Vlachos, D. Kugiumtzis, "State Space Reconstruction for Multivariate Time Series Prediction", Nonlinear Phenomena in Complex Systems, Vol 11, No 2, pp 241-249, 2008.

[4] Kantz, H., and Schreiber, T. Nonlinear Time Series Analysis. Cambridge: Cambridge University Press, Vol. 7, 2004.

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用に関するメモと制限:

• プロットを生成する構文は、コード生成ではサポートされません。

バージョン履歴

R2018a で導入

参考

approximateEntropy | lyapunovExponent | correlationDimension