lyapunovExponent

限りなく近い軌跡の分離率の特徴付け

構文

lyapExp = lyapunovExponent(X,fs)

lyapExp = lyapunovExponent(X,fs,lag)

lyapExp = lyapunovExponent(X,fs,[],dim)

lyapExp = lyapunovExponent(X,fs,lag,dim)

[lyapExp,estep,ldiv] = lyapunovExponent(___)

___ = lyapunovExponent(___,Name,Value)

lyapunovExponent(___)

説明

lyapExp = lyapunovExponent(X,fs) は、サンプリング周波数 fs を使用して、等間隔にサンプリングされた時間領域信号 X のリアプノフ指数を推定します。lyapunovExponent を使用して、位相空間での限りなく近い軌跡の分離率を特徴付け、異なるアトラクターを区別します。リアプノフ指数は、システムにおける無秩序性のレベルの定量化に役立ち、潜在的な故障の検出に使用できます。

lyapExp = lyapunovExponent(X,fs,lag) は、時間遅延 lag に対するリアプノフ指数を推定します。

lyapExp = lyapunovExponent(X,fs,[],dim) は、埋め込み次元 dim に対するリアプノフ指数を推定します。

lyapExp = lyapunovExponent(X,fs,lag,dim) は、時間遅延 lag と埋め込み次元 dim に対するリアプノフ指数を推定します。

[lyapExp,estep,ldiv] = lyapunovExponent(___) は、等間隔にサンプリングされた時間領域信号 X のリアプノフ指数、拡大ステップ、および対応する対数発散を推定します。信号の診断には、拡大ステップ estep と、対応する対数発散 ldiv を使用します。

___ = lyapunovExponent(___,Name,Value) は、1 つ以上の Name,Value ペア引数で指定された追加オプションを使用して、リアプノフ指数を推定します。

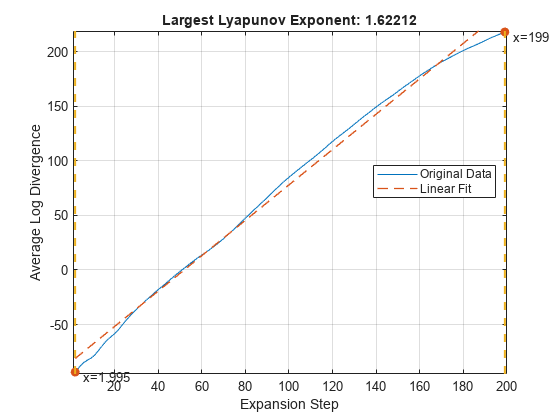
出力引数のない lyapunovExponent(___) は、平均対数発散対拡大ステップのプロットを作成します。

生成された対話型プロットを使って、適切な ExpansionRange を探します。

例

リアプノフ指数の可視化と推定

この例では、無秩序解の一意のセットを記述するローレンツ アトラクターについて検討します。

データ セットとサンプリング周波数 fs をワークスペースに読み込み、ローレンツ アトラクターを 3-D で可視化します。

load('lorenzAttractorExampleData.mat','data','fs');
plot3(data(:,1),data(:,2),data(:,3));

この例では、ローレンツ アトラクターの x 方向のデータを使用します。Lag は不明であるため、phaseSpaceReconstruction を用いて遅延を推定します。ローレンツ アトラクターは 3 次元系であるため、次元を 3 に設定します。dim パラメーターと lag パラメーターは、平均対数発散対拡大ステップのプロットを作成するために必要です。

xdata = data(:,1);
dim = 3;
[~,lag] = phaseSpaceReconstruction(xdata,[],dim)

lag = 10

前のステップで得られた lag の値を用いて、ローレンツ アトラクターの平均対数発散対拡大ステップのプロットを作成します。すべての拡大ステップをキャプチャするために、十分に大きな拡大範囲を設定します。

eRange = 200;
lyapunovExponent(xdata,fs,lag,dim,'ExpansionRange',eRange)

1 本目の緑の垂直破線 (左側) は、拡大範囲を推定するための最小ステップ数、2 本目の緑の垂直破線 (右側) は、最大ステップ数を示しています。1 本目と 2 本目の垂直線は、2 本合わせて拡大範囲を示しています。赤の破線は、拡大範囲内で、データに対する線形近似線を示しています。

最大のリアプノフ指数を計算するには、まず、正確な推定に必要な拡大範囲を決定する必要があります。

プロットで 2 本の緑の垂直破線をドラッグして、元のデータ線に線形近似線を "最適適合" させ、拡大範囲 ${\mathit{K}}_{\min }$ と ${\mathit{K}}_{\max }$ を求めます。

2 本の垂直線をドラッグして適切に適合させた後の、拡大範囲の新しい値を確認します。

拡大範囲は 0 または正の整数でしか指定できないため、${\mathit{K}}_{\min }$ と ${\mathit{K}}_{\max }$ を丸めて最も近い整数を指定します。新しい拡大範囲の値を用いて、ローレンツ アトラクターの最大のリアプノフ指数を求めます。

Kmin = 21;
Kmax = 161;
lyapExp = lyapunovExponent(xdata,fs,lag,dim,'ExpansionRange',[Kmin Kmax])

lyapExp = 1.6834

負のリアプノフ指数は収束を示し、正のリアプノフ指数は発散や無秩序性を示します。lyapExp の振幅は、限りなく近い軌跡の収束または発散の速度を示す指標です。

入力引数

X — 等間隔にサンプリングされた時間領域信号

ベクトル | 配列 | timetable

等間隔にサンプリングされた時間領域信号。ベクトル、配列、timetable のいずれかで指定します。X が複数列の場合、lyapunovExponent は X を多変量信号として扱い、最大リアプノフ指数を計算します。

X が行ベクトルとして指定された場合、lyapunovExponent はこれを一変量信号として扱います。

fs — サンプリング周波数

スカラー

サンプリング周波数。スカラーとして指定します。サンプリング周波数またはサンプル レートは、1 秒間に得られるサンプルの平均数です。

fs が渡されない場合は、正規化周波数 2π がリアプノフ指数の計算に使用されます。X が timetable として指定された場合は、そこからサンプリング時間が推定されます。

dim — 埋め込み次元

スカラー | ベクトル

埋め込み次元。スカラーまたはベクトルとして指定します。dim は 'Dimension' の名前と値のペアと等価です。

lag — 時間遅延

スカラー | ベクトル

時間遅延。スカラーまたはベクトルとして指定します。lag は'Lag' の名前と値のペアと等価です。

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペア自体は順不同で構いません。

R2021a 以前は、名前と値をそれぞれコンマで区切り、 Name を引用符で囲みます。

例: …,'Dimension',3

Dimension — 埋め込み次元

2 (既定値) | スカラー | ベクトル

埋め込み次元。'Dimension' とスカラーまたはベクトルのいずれかで構成されるコンマ区切りのペアとして指定します。Dimension がスカラーである場合は、X の各列は、Dimension を使用して再構成されます。X の列数と同じ長さのベクトルを Dimension としたとき、列 i の再構成次元は Dimension(i) になります。

システムの次元、つまり状態数に基づいて Dimension を指定します。埋め込み次元の詳細については、phaseSpaceReconstruction を参照してください。

Lag — 位相空間の再構成の遅延

1 (既定値) | スカラー | ベクトル

位相空間の再構成の遅延。'Lag' とスカラーまたはベクトルのいずれかで構成されるコンマ区切りのペアで指定します。Lag がスカラーである場合は、X の各列は、Lag を使用して再構成されます。X の列数と同じ長さのベクトルを Lag としたとき、列 i の再構成の遅延は Lag(i) になります。

Lag の既定値は 1 です。

遅延が小さすぎると、データにランダム ノイズが入ります。一方、ラグが大きすぎると、再構成されたダイナミクスは時系列の真のダイナミクスを表しません。最適な遅延の推定の詳細については、phaseSpaceReconstruction を参照してください。

MinSeparation — 平均周期

ceil(fs/max(meanfreq(X,fs))) (既定値) | 正のスカラー整数

平均周期。'MinSeparation' と正のスカラー整数で構成されるコンマ区切りのペアとして指定します。

MinSeparation は、最大リアプノフ指数を推定するために、点 i の最近傍 i^* を見つけるために使用されるしきい値です。

MinSeparation の既定値は ceil(fs/max(meanfreq(X,fs))) です。

ExpansionRange — 拡大ステップの範囲

[1, 5] (既定値) | 1 行 2 列の正の整数配列 | 正のスカラー整数

拡大ステップの範囲。'ExpansionRange' と 1 行 2 列の正の整数配列または正のスカラー整数のいずれかで構成されるコンマ区切りのペアとして指定します。

ExpansionRate の最小値と最大値は、リアプノフ指数を計算するローカルの拡大率の推定に使用されます。

ExpansionRange がスカラー M で指定された場合は、その範囲は [1, M] に設定されます。ExpansionRange は正の整数のみで指定でき、既定値は [1, 5] です。

出力引数

lyapExp — 最大リアプノフ指数

スカラー

最大リアプノフ指数。スカラーとして返されます。lyapExp は、位相空間における限りなく近い軌跡の発散および収束率を定量化します。

負のリアプノフ指数は収束を示し、正のリアプノフ指数は発散や無秩序性を示します。lyapExp の振幅は、限りなく近い軌跡の収束または発散の速度を示す指標です。

データ セット内の発散を識別する機能は、工学分野では部品の振動や音響信号を調べて故障を推定したり、船の動きから転覆を予測したりするうえで役立ちます。[2][3]

estep — 推定に使用される拡大ステップ

配列

推定に使用される拡大ステップ。配列として返されます。estep は、ExpansionRange の最大値で定義される同数のポイントに分割された拡大範囲の最大値と最小値の差です。

ldiv — 対数発散

配列

対数発散。estep と同じ大きさの配列として返されます。ldiv の各値の大きさは、estep の各点の対数収束または対数発散に対応します。

アルゴリズム

リアプノフ指数は、以下の方法で計算されます。

1. まず、関数 lyapunovExponent が、埋め込み次元 m とラグ τ を持つ、遅延した再構成 Y_1:N を生成します。

2. ある点 i に対して、平均周期 MinSeparation を平均周波数の逆数としたとき、$$\left|i-i^{*}\right|>MinSeparation$$ となるような $$\underset{i^{*}}{\min }\Vert Y_i-Y_{i^{*}}\Vert$$ を満たす最近傍点 i^* を求めます。

3. [1]は、全拡大範囲のリアプノフ指数を次のように計算します。

   $$\lambda (i)=\frac{1}{\left(K_{\max }-K_{\min }+1\right)dt}{\displaystyle \sum _{K=K_{\min }}^{K_{\max }}\frac{1}{K}\ln \frac{\Vert Y_{i+K}-Y_{i^{*}+K}\Vert }{\Vert Y_i-Y_{i^{*}}\Vert }}$$

   ここで、K_min および K_max は ExpansionRange、dt はサンプリング時間を表し、次の式が成り立ちます。$$ldiv=\ln \frac{\Vert Y_{i+K}-Y_{i^{*}+K}\Vert }{\Vert Y_i-Y_{i^{*}}\Vert }$$

4. リアプノフ指数の 1 つの値は、polyfit コマンドを使用して、前の手順から次のように計算されます。

   $$lyapExp\text{ = }polyfit\left(\left[K_{\min }{K}_{\max }\right],\lambda (i)\right)$$

参照

[1] Michael T. Rosenstein , James J. Collins , Carlo J. De Luca. "A practical method for calculating largest Lyapunov exponents from small data sets ". Physica D 1993. Volume 65. Pages 117-134.

[2] Caesarendra, Wahyu & Kosasih, P & Tieu, Kiet & Moodie, Craig. "An application of nonlinear feature extraction-A case study for low speed slewing bearing condition monitoring and prognosis." IEEE/ASME International Conference on Advanced Intelligent Mechatronics: Mechatronics for Human Wellbeing, AIM 2013.1713-1718. 10.1109/AIM.2013.6584344.

[3] McCue, Leigh & W. Troesch, Armin. (2011). "Use of Lyapunov Exponents to Predict Chaotic Vessel Motions". Fluid Mechanics and its Applications. 97. 415-432. 10.1007/978-94-007-1482-3_23.

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用に関するメモと制限:

• プロットを生成する構文は、コード生成ではサポートされません。

バージョン履歴

R2018a で導入

参考

approximateEntropy | correlationDimension | phaseSpaceReconstruction