このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

pagesvd

ページ単位の特異値分解

R2021b 以降

構文

S = pagesvd(X)

[U,S,V] = pagesvd(X)

[___] = pagesvd(X,"econ")

[___] = pagesvd(___,outputForm)

説明

S = pagesvd(X) は、多次元配列の各ページの特異値を返します。出力の各ページ S(:,:,i) は、X(:,:,i) の特異値を降順に格納した列ベクトルです。X の各ページが m 行 n 列の行列の場合、S の各ページで返される特異値の数は min(m,n) です。

[U,S,V] = pagesvd(X) は、多次元配列の各ページの特異値分解を計算します。出力配列のページは U(:,:,i) * S(:,:,i) * V(:,:,i)' = X(:,:,i) を満たします。

S のサイズは X と同じで、S の各ページは非負の特異値の降順の対角行列です。U と V のページはユニタリ行列です。

X が 3 次元より大きい場合、pagesvd は U(:,:,i,j,k) * S(:,:,i,j,k) * V(:,:,i,j,k)' = X(:,:,i,j,k) のように同じ次元数の配列を返します。

[___] = pagesvd(X,"econ") は、前述の出力引数のいずれかの組み合わせを使用して、X のページのエコノミーサイズの分解を生成します。X が m×n×p の配列の場合、次のようになります。

• m > n — U の各ページの最初の n 列のみが計算され、S のサイズは n×n×p になります。

• m = n — pagesvd(X,"econ") は pagesvd(X) と等価です。

• m < n — V の各ページの最初の m 列のみが計算され、S のサイズは m×m×p になります。

エコノミーサイズの分解により、S の特異値のページにある余分なゼロの行または列が、式 U(:,:,i) * S(:,:,i) * V(:,:,i)' でこれらのゼロに乗算される U または V の列とともに削除されます。これらのゼロと列を削除すると、分解の精度を損なわずに、実行時間を改善してストレージ要件を低減することができます。

[___] = pagesvd(___,outputForm) は、S で返される特異値の出力形式を指定します。このオプションは、前述のすべての入力引数または出力引数の組み合わせで使用できます。S の各ページを列ベクトルとして返す場合は "vector"、S の各ページを対角行列として返す場合は "matrix" を指定します。

例

配列ページの特異値

6 行 6 列の行列を 2 つ作成します。関数 cat を使用して、それらを 3 番目の次元に沿って 6×6×2 の配列に連結します。

A = magic(6);
B = hilb(6);
X = cat(3,A,B);

出力を 1 つ指定して pagesvd を呼び出し、各ページの特異値を計算します。

S = pagesvd(X)

S = 
S(:,:,1) =

  111.0000
   50.6802
   34.3839
   10.1449
    5.5985
    0.0000


S(:,:,2) =

    1.6189
    0.2424
    0.0163
    0.0006
    0.0000
    0.0000

配列ページの特異値分解

5 行 5 列の行列を 2 つ作成します。関数 cat を使用して、それらを 3 番目の次元に沿って 5×5×2 の配列に連結します。

A = magic(5);
B = hilb(5);
X = cat(3,A,B);

各配列ページの特異値を計算します。

s = pagesvd(X)

s = 
s(:,:,1) =

   65.0000
   22.5471
   21.6874
   13.4036
   11.9008


s(:,:,2) =

    1.5671
    0.2085
    0.0114
    0.0003
    0.0000

各配列ページに対して完全な特異値分解を実行します。

[U,S,V] = pagesvd(X)

U = 
U(:,:,1) =

   -0.4472   -0.5456    0.5117    0.1954   -0.4498
   -0.4472   -0.4498   -0.1954   -0.5117    0.5456
   -0.4472   -0.0000   -0.6325    0.6325    0.0000
   -0.4472    0.4498   -0.1954   -0.5117   -0.5456
   -0.4472    0.5456    0.5117    0.1954    0.4498


U(:,:,2) =

   -0.7679    0.6019   -0.2142    0.0472    0.0062
   -0.4458   -0.2759    0.7241   -0.4327   -0.1167
   -0.3216   -0.4249    0.1205    0.6674    0.5062
   -0.2534   -0.4439   -0.3096    0.2330   -0.7672
   -0.2098   -0.4290   -0.5652   -0.5576    0.3762

S = 
S(:,:,1) =

   65.0000         0         0         0         0
         0   22.5471         0         0         0
         0         0   21.6874         0         0
         0         0         0   13.4036         0
         0         0         0         0   11.9008


S(:,:,2) =

    1.5671         0         0         0         0
         0    0.2085         0         0         0
         0         0    0.0114         0         0
         0         0         0    0.0003         0
         0         0         0         0    0.0000

V = 
V(:,:,1) =

   -0.4472   -0.4045    0.2466   -0.6627    0.3693
   -0.4472   -0.0056    0.6627    0.2466   -0.5477
   -0.4472    0.8202   -0.0000   -0.0000    0.3568
   -0.4472   -0.0056   -0.6627   -0.2466   -0.5477
   -0.4472   -0.4045   -0.2466    0.6627    0.3693


V(:,:,2) =

   -0.7679    0.6019   -0.2142    0.0472    0.0062
   -0.4458   -0.2759    0.7241   -0.4327   -0.1167
   -0.3216   -0.4249    0.1205    0.6674    0.5062
   -0.2534   -0.4439   -0.3096    0.2330   -0.7672
   -0.2098   -0.4290   -0.5652   -0.5576    0.3762

各配列ページについて、マシンの精度内で $\mathit{X}=\mathit{U}\mathit{S}{\mathit{V}}^{\mathit{H}}$ の関係が成り立つことを確認します。

e1 = norm(X(:,:,1) - U(:,:,1)*S(:,:,1)*V(:,:,1)',"fro")

e1 = 7.4110e-14

e2 = norm(X(:,:,2) - U(:,:,2)*S(:,:,2)*V(:,:,2)',"fro")

e2 = 4.3111e-16

あるいは、pagemtimes を使用して両方のページの関係を同時に確認することもできます。

US = pagemtimes(U,S);
USV = pagemtimes(US,"none",V,"ctranspose");
e = max(abs(X - USV),[],"all")

e = 2.9310e-14

特異値の出力形式の制御

6 行 6 列の行列を 2 つ作成します。関数 cat を使用して、それらを 3 番目の次元に沿って 6×6×2 の配列に連結します。

A = magic(6);
B = hilb(6);
X = cat(3,A,B);

各配列ページの SVD を計算します。既定では、出力を複数指定した場合、pagesvd は特異値の各ページを対角行列として返します。

[U,S,V] = pagesvd(X)

U = 
U(:,:,1) =

   -0.4082    0.5574    0.0456   -0.4182    0.3092    0.5000
   -0.4082   -0.2312    0.6301   -0.2571   -0.5627    0.0000
   -0.4082    0.4362    0.2696    0.5391    0.1725   -0.5000
   -0.4082   -0.3954   -0.2422   -0.4590    0.3971   -0.5000
   -0.4082    0.1496   -0.6849    0.0969   -0.5766    0.0000
   -0.4082   -0.5166   -0.0182    0.4983    0.2604    0.5000


U(:,:,2) =

   -0.7487    0.6145   -0.2403   -0.0622    0.0111   -0.0012
   -0.4407   -0.2111    0.6977    0.4908   -0.1797    0.0356
   -0.3207   -0.3659    0.2314   -0.5355    0.6042   -0.2407
   -0.2543   -0.3947   -0.1329   -0.4170   -0.4436    0.6255
   -0.2115   -0.3882   -0.3627    0.0470   -0.4415   -0.6898
   -0.1814   -0.3707   -0.5028    0.5407    0.4591    0.2716

S = 
S(:,:,1) =

  111.0000         0         0         0         0         0
         0   50.6802         0         0         0         0
         0         0   34.3839         0         0         0
         0         0         0   10.1449         0         0
         0         0         0         0    5.5985         0
         0         0         0         0         0    0.0000


S(:,:,2) =

    1.6189         0         0         0         0         0
         0    0.2424         0         0         0         0
         0         0    0.0163         0         0         0
         0         0         0    0.0006         0         0
         0         0         0         0    0.0000         0
         0         0         0         0         0    0.0000

V = 
V(:,:,1) =

   -0.4082    0.6234   -0.3116    0.2495    0.2511    0.4714
   -0.4082   -0.6282    0.3425    0.1753    0.2617    0.4714
   -0.4082   -0.4014   -0.7732   -0.0621   -0.1225   -0.2357
   -0.4082    0.1498    0.2262   -0.4510    0.5780   -0.4714
   -0.4082    0.1163    0.2996    0.6340   -0.3255   -0.4714
   -0.4082    0.1401    0.2166   -0.5457   -0.6430    0.2357


V(:,:,2) =

   -0.7487    0.6145   -0.2403   -0.0622    0.0111   -0.0012
   -0.4407   -0.2111    0.6977    0.4908   -0.1797    0.0356
   -0.3207   -0.3659    0.2314   -0.5355    0.6042   -0.2407
   -0.2543   -0.3947   -0.1329   -0.4170   -0.4436    0.6255
   -0.2115   -0.3882   -0.3627    0.0470   -0.4415   -0.6898
   -0.1814   -0.3707   -0.5028    0.5407    0.4591    0.2716

"vector" オプションを指定して、特異値の各ページを列ベクトルとして返します。

[U,S,V] = pagesvd(X,"vector")

U = 
U(:,:,1) =

   -0.4082    0.5574    0.0456   -0.4182    0.3092    0.5000
   -0.4082   -0.2312    0.6301   -0.2571   -0.5627    0.0000
   -0.4082    0.4362    0.2696    0.5391    0.1725   -0.5000
   -0.4082   -0.3954   -0.2422   -0.4590    0.3971   -0.5000
   -0.4082    0.1496   -0.6849    0.0969   -0.5766    0.0000
   -0.4082   -0.5166   -0.0182    0.4983    0.2604    0.5000


U(:,:,2) =

   -0.7487    0.6145   -0.2403   -0.0622    0.0111   -0.0012
   -0.4407   -0.2111    0.6977    0.4908   -0.1797    0.0356
   -0.3207   -0.3659    0.2314   -0.5355    0.6042   -0.2407
   -0.2543   -0.3947   -0.1329   -0.4170   -0.4436    0.6255
   -0.2115   -0.3882   -0.3627    0.0470   -0.4415   -0.6898
   -0.1814   -0.3707   -0.5028    0.5407    0.4591    0.2716

S = 
S(:,:,1) =

  111.0000
   50.6802
   34.3839
   10.1449
    5.5985
    0.0000


S(:,:,2) =

    1.6189
    0.2424
    0.0163
    0.0006
    0.0000
    0.0000

V = 
V(:,:,1) =

   -0.4082    0.6234   -0.3116    0.2495    0.2511    0.4714
   -0.4082   -0.6282    0.3425    0.1753    0.2617    0.4714
   -0.4082   -0.4014   -0.7732   -0.0621   -0.1225   -0.2357
   -0.4082    0.1498    0.2262   -0.4510    0.5780   -0.4714
   -0.4082    0.1163    0.2996    0.6340   -0.3255   -0.4714
   -0.4082    0.1401    0.2166   -0.5457   -0.6430    0.2357


V(:,:,2) =

   -0.7487    0.6145   -0.2403   -0.0622    0.0111   -0.0012
   -0.4407   -0.2111    0.6977    0.4908   -0.1797    0.0356
   -0.3207   -0.3659    0.2314   -0.5355    0.6042   -0.2407
   -0.2543   -0.3947   -0.1329   -0.4170   -0.4436    0.6255
   -0.2115   -0.3882   -0.3627    0.0470   -0.4415   -0.6898
   -0.1814   -0.3707   -0.5028    0.5407    0.4591    0.2716

S = pagesvd(X) のように出力引数を 1 つ指定した場合、pagesvd の動作が切り替わり、既定では列ベクトルで特異値の各ページが返されます。その場合は、"matrix" オプションを指定すると、特異値の各ページを対角行列として返すことができます。

方形行列のエコノミーサイズの分解

ランダムな整数の要素をもつ 10 行 3 列の行列を作成します。

X = randi([0 3],10,3);

行列に対して完全な分解とエコノミーサイズの分解の両方を実行します。

[U,S,V] = pagesvd(X)

U = 10×10

   -0.2554   -0.1828    0.6086   -0.6120   -0.0623   -0.2365   -0.1841    0.0165   -0.2369   -0.0792
   -0.3408    0.4291    0.0365    0.1237   -0.2953    0.3040    0.0346   -0.3966   -0.3014   -0.5041
   -0.3018   -0.3274   -0.6272   -0.0847   -0.3313   -0.3920   -0.2374   -0.2006   -0.1896    0.0717
   -0.3560   -0.2919    0.3996    0.7531   -0.0136   -0.1963   -0.1046    0.0518   -0.0521    0.0788
   -0.3711   -0.0109   -0.1957   -0.0519    0.8784    0.0025   -0.0413   -0.1224   -0.1273   -0.1289
   -0.1298   -0.5635   -0.0331   -0.0842   -0.0685    0.7933   -0.1005    0.0004   -0.0259    0.1119
   -0.2002   -0.2327   -0.0099   -0.0782   -0.0595   -0.0962    0.9398   -0.0274   -0.0524    0.0117
   -0.3278    0.1769   -0.1847   -0.0238   -0.0987    0.0714   -0.0078    0.8775   -0.1186   -0.1662
   -0.4273    0.0534    0.0145   -0.1222   -0.0872   -0.0131   -0.0467   -0.0828    0.8772   -0.1140
   -0.3408    0.4291    0.0365   -0.0661   -0.0416    0.1247    0.0203   -0.0831   -0.1055    0.8114

S = 10×3

   10.9594         0         0
         0    4.6820         0
         0         0    3.4598
         0         0         0
         0         0         0
         0         0         0
         0         0         0
         0         0         0
         0         0         0
         0         0         0

V = 3×3

   -0.6167    0.3011    0.7274
   -0.6282    0.3686   -0.6852
   -0.4744   -0.8795   -0.0382

[Ue,Se,Ve] = pagesvd(X,"econ")

Ue = 10×3

   -0.2554   -0.1828    0.6086
   -0.3408    0.4291    0.0365
   -0.3018   -0.3274   -0.6272
   -0.3560   -0.2919    0.3996
   -0.3711   -0.0109   -0.1957
   -0.1298   -0.5635   -0.0331
   -0.2002   -0.2327   -0.0099
   -0.3278    0.1769   -0.1847
   -0.4273    0.0534    0.0145
   -0.3408    0.4291    0.0365

Se = 3×3

   10.9594         0         0
         0    4.6820         0
         0         0    3.4598

Ve = 3×3

   -0.6167    0.3011    0.7274
   -0.6282    0.3686   -0.6852
   -0.4744   -0.8795   -0.0382

エコノミーサイズの分解では、pagesvd で Ue の最初の 3 列のみが計算され、Se は 3 行 3 列になります。

入力引数

X — 入力配列

行列 | 多次元配列

入力配列。行列または多次元配列として指定します。

データ型: single | double
複素数のサポート: あり

outputForm — 特異値の出力形式

"vector" | "matrix"

特異値の出力形式。次の値のいずれかとして指定します。

• "vector" — S の各ページは列ベクトルになります。これは、S = pagesvd(X) のように出力を 1 つ指定する場合の既定の動作です。

• "matrix" — S の各ページは対角行列になります。これは、[U,S,V] = pagesvd(X) のように出力を複数指定する場合の既定の動作です。

例: [U,S,V] = pagesvd(X,"vector") は、S のページを対角行列ではなく列ベクトルとして返します。

例: S = pagesvd(X,"matrix") は、S のページを列ベクトルではなく対角行列として返します。

データ型: char | string

出力引数

U — 左特異ベクトル

多次元配列

左特異ベクトル。多次元配列として返されます。各ページ U(:,:,i) は、X(:,:,i) の左特異ベクトルを列の要素とする行列です。

• m 行 n 列の行列 X(:,:,i) で m > n の場合、エコノミーサイズの分解 pagesvd(X,"econ") は、U の各ページの最初の n 列のみを計算します。この場合、U(:,:,i) の列は直交であり、U(:,:,i) は $$U^{H}U=I_n$$ を満たす m 行 n 列の行列です。

• それ以外の場合、pagesvd(X) は各ページ U(:,:,i) を $$U{U}^H=U^{H}U=I_m$$ を満たす m 行 m 列のユニタリ行列として返します。非ゼロの特異値に対応する U(:,:,i) の列は、X(:,:,i) の値域に対応する一連の正規直交基底ベクトルを構成します。

マシンや MATLAB^® のリリースが異なると、異なった特異ベクトルが生成されることがありますが、数値的にはいずれも正確です。U(:,:,i) と V(:,:,i) の対応する列で符号が反転する場合がありますが、これは、反転しても式 U(:,:,i) * S(:,:,i) * V(:,:,i)' の値には影響がないためです。

S — 特異値

多次元配列

特異値。多次元配列として返されます。各ページ S(:,:,i) に X(:,:,i) の特異値が降順に格納されます。

m 行 n 列の行列 X(:,:,i) の場合、次のようになります。

• エコノミーサイズの分解 [U,S,V] = pagesvd(X,"econ") は、次数 min([m,n]) の正方行列 S(:,:,i) を返します。

• 完全な分解 [U,S,V] = pagesvd(X) は、X と同じサイズの S を返します。

さらに、S の各ページの特異値は、pagesvd の呼び出し方法と outputForm オプションの指定に応じて列ベクトルまたは対角行列のいずれかとして返されます。

• pagesvd の呼び出しで出力を 1 つ指定した場合または "vector" オプションを指定した場合、S の各ページは列ベクトルになります。

• pagesvd の呼び出しで出力を複数指定した場合または "matrix" オプションを指定した場合、S の各ページは対角行列になります。

V — 右特異ベクトル

多次元配列

右特異ベクトル。多次元配列として返されます。各ページ V(:,:,i) は、X(:,:,i) の右特異ベクトルを列の要素とする行列です。

• m 行 n 列の行列 X(:,:,i) で m < n の場合、エコノミーサイズの分解 pagesvd(X,"econ") は、V の各ページの最初の m 列のみを計算します。この場合、V(:,:,i) の列は直交であり、V(:,:,i) は $$V^{H}V=I_m$$ を満たす n 行 m 列の行列です。

• それ以外の場合、pagesvd(X) は各ページ V(:,:,i) を $$V{V}^H=V^{H}V=I_n$$ を満たす n 行 n 列のユニタリ行列として返します。非ゼロの特異値に "対応しない" V(:,:,i) の列は、X(:,:,i) のヌル空間の一連の正規直交基底ベクトルを構成します。

マシンや MATLAB のリリースが異なると、異なった特異ベクトルが生成されることがありますが、数値的にはいずれも正確です。U(:,:,i) と V(:,:,i) の対応する列で符号が反転する場合がありますが、これは、反転しても式 U(:,:,i) * S(:,:,i) * V(:,:,i)' の値には影響がないためです。

詳細

配列ページ

pagesvd のようなページ単位関数は、多次元配列に配置された 2 次元行列を処理します。たとえば 3-D 配列では、配列の 3 番目の次元にある要素は、本のページのようにお互いの上に積み重なるため、一般に "ページ" と呼ばれています。各ページは関数によって処理される行列です。

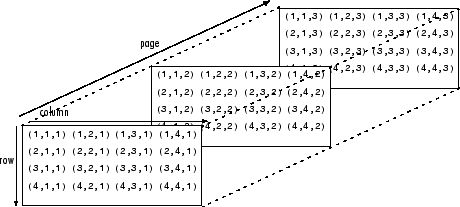
2 次元行列の集合から、4 次元配列または 5 次元配列のような、より高い次元の配列も作成できます。この場合でも、pagesvd は配列の基本単位を X(:,:,i,j,k,l) などの処理される 2 次元行列として扱います。

関数 cat は、行列の集合から多次元配列を作成するのに便利です。関数 zeros は、多次元配列を事前に割り当てるのに便利です。

ヒント

• pagesvd を使用して取得した結果は、for ループで同じ行列のそれぞれの特異値分解を計算することと数値的に等価です。ただし、浮動小数点の丸め誤差のため、2 つの結果が若干異なることがあります。

拡張機能

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

使用上の注意事項および制限事項:

• 入力配列の行と列のサイズは 32 まででなければなりません。

詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

分散配列

Parallel Computing Toolbox™ を使用して、クラスターの結合メモリ上で大きなアレイを分割します。

この関数は分散配列を完全にサポートしています。詳細については、分散配列を使用した MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2021b で導入

参考

svd | pagemtimes | pagetranspose | pagectranspose

トピック

• 特異値
• 多次元配列