特異値

方形行列 A の "特異値" と対応する "特異ベクトル" は、スカラー σ と u と v の 1 組のベクトルで表され、次の式を満たします。

$$\begin{array}{l}Av=\sigma u\\ A^{H}u=\sigma v,\end{array}$$

ここで、$$A^H$$ は A のエルミート転置です。通常、特異ベクトル u と v はノルムが 1 になるようにスケーリングされます。また、u と v が A の特異ベクトルである場合は、-u と -v も A の特異ベクトルです。

特異値 σ は、A が複素数であっても、常に非負の実数です。対角行列 Σ に特異値を配置します。これに対応する特異ベクトルは 2 つの直交行列 U と V の列からなり、次のような方程式が導出されます。

$$\begin{array}{l}AV=U\Sigma \\ A^{H}U=V\Sigma .\end{array}$$

U と V はユニタリ行列であるため、最初の方程式に右側から $$V^H$$ を乗算すると、特異値分解の方程式が導出されます。

$$A=U\Sigma V^H.$$

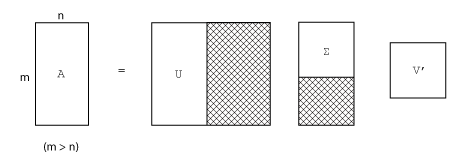
m 行 n 列の行列の完全な特異値分解は、次で表されます。

• m 行 m 列の行列 U

• m 行 n 列の行列 Σ

• n 行 n 列の行列 V

言い換えれば U と V は共に正方で、Σ は A と同じサイズです。A の行数が列数よりずっと多い場合 (m > n)、結果の m 行 m 列の行列 U は大きくなります。ただし、U のほとんどの列は Σ のゼロで乗算されます。このような場合 "エコノミー サイズ" で分解すると、m 行 n 列の U、n 行 n 列の Σ、同じ V が作成され、計算時間もメモリ サイズも節約されます。

常微分方程式を表現する場合ように、あるベクトル空間内でマッピングを行う場合、固有値分解はその行列の解析に適切な方法になります。ただし、あるベクトル空間から他のベクトル空間へマッピングする行列を解析する場合は特異値分解が適切な方法になります。特異値分解は異なる次元についても扱えます。ほとんどの連立線形方程式は、この 2 番目の方法のカテゴリに入ります。

A が正方、対称、かつ正定値の場合は、この固有値分解と特異値分解は等しくなります。ただし A が対称および正定値でない場合、2 つの分解の結果のズレは大きくなります。特に実数行列の特異値分解は常に実数ですが、実数の非対称行列の固有値分解は複素数になることもあります。

例として行列を作成します。

A = [9     4
     6     8
     2     7];

A に対して非スパースな特異値分解は次のようになります。

[U,S,V] = svd(A)

U =

   -0.6105    0.7174    0.3355
   -0.6646   -0.2336   -0.7098
   -0.4308   -0.6563    0.6194


S =

   14.9359         0
         0    5.1883
         0         0


V =

   -0.6925    0.7214
   -0.7214   -0.6925

U*S*V' が丸め誤差の範囲内で A に等しいことが確かめられます。このような小さな行列の問題をエコノミー サイズで分解すると、わずかですが使用メモリ サイズを小さくできます。

[U,S,V] = svd(A,"econ")

U =

   -0.6105    0.7174
   -0.6646   -0.2336
   -0.4308   -0.6563


S =

   14.9359         0
         0    5.1883


V =

   -0.6925    0.7214
   -0.7214   -0.6925

U*S*V' が丸め誤差の範囲内で A に等しいことを再確認できます。

SVD 計算のバッチ処理

同じサイズの行列の大規模な集合を分解する必要がある場合、svd を使用してすべての分解をループで実行するのは非効率的です。代わりに、すべての行列を多次元配列に連結して pagesvd を使用すると、単一の関数呼び出しですべての配列ページの特異値分解を実行できます。

関数	使用方法
pagesvd	関数 pagesvd を使用して、多次元配列のページで特異値分解を実行します。これは、すべて同じサイズの行列の大規模な集合で SVD を実行する効率的な方法です。

たとえば、2 行 2 列の 3 つの行列の集合について考えてみます。関数 cat を使用して、行列を 2 x 2 x 3 の配列に連結します。

A = [0 -1; 1 0];
B = [-1 0; 0 -1];
C = [0 1; -1 0];
X = cat(3,A,B,C);

次に、pagesvd を使用して、3 つの分解を同時に実行します。

[U,S,V] = pagesvd(X);

X の各ページに、出力 U、S、および V の対応するページがあります。たとえば、行列 A は X の最初のページにあり、その分解は U(:,:,1)*S(:,:,1)*V(:,:,1)' で与えられます。

SVD による低ランク近似

大規模なスパース行列では、svd を使用して "すべて" の特異値と特異ベクトルを計算することは、必ずしも現実的ではありません。たとえば、最も大きい特異値をいくつかだけ知る必要がある場合に、5000 行 5000 列のスパース行列の特異値をすべて計算するのは余分な作業となります。

特異値と特異ベクトルのサブセットのみが必要な場合は、関数 svd よりも、関数 svds と関数 svdsketch が推奨されます。

関数	使用方法
svds	svds を使用して、SVD によるランク k の近似を計算します。特異値のサブセットを最大にするか、最小にするか、特定の数に最も近くするかを指定できます。svds は一般的に、ランク k の最適な近似を計算します。
svdsketch	svdsketch を使用して、指定された許容誤差を満たす、入力行列の部分的な SVD を計算します。svds ではランクを指定する必要がありますが、svdsketch では指定された許容誤差に基づき、行列スケッチのランクが適応的に特定されます。svdsketch が最終的に使用するランク k の近似は許容誤差を満たしますが、svds と異なり、最適なものであることは保証されません。

たとえば、密度が約 30% である、1000 行 1000 列のランダムなスパース行列について考えてみます。

n = 1000;
A = sprand(n,n,0.3);

6 つの最大特異値は次のようになります。

S = svds(A)

S =

  130.2184
   16.4358
   16.4119
   16.3688
   16.3242
   16.2838

また、6 つの最小特異値は次のようになります。

S = svds(A,6,"smallest")

S =

    0.0740
    0.0574
    0.0388
    0.0282
    0.0131
    0.0066

行列が比較的小さく、完全な行列 full(A) としてメモリに収まる場合は、svds や svdsketch よりも svd(full(A)) を使用するほうが依然として高速になることがあります。ただし、非常に大規模なスパース行列の場合は、svds や svdsketch の使用が必要になります。

参考

svd | svds | svdsketch | gsvd | pagesvd

トピック

• MATLAB 環境の行列
• 分解
• 固有値