fsurf

3 次元表面をプロット

• 

×

構文

fsurf(f)

fsurf(f,xyinterval)

fsurf(funx,funy,funz)

fsurf(funx,funy,funz,uvinterval)

fsurf(___,LineSpec)

fsurf(___,Name,Value)

fsurf(ax,___)

fs = fsurf(___)

説明

fsurf(f) は、x と y の既定の区間 [-5 5] に関数 z = f(x,y) の表面プロットを作成します。

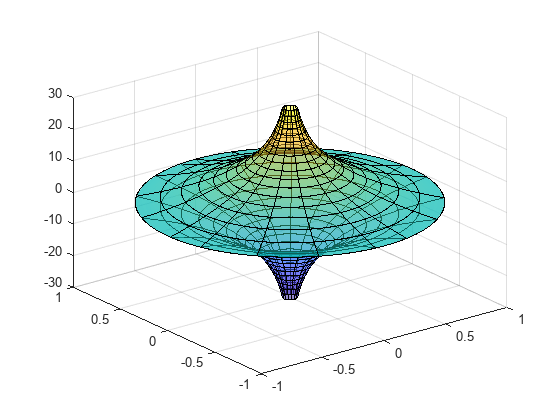
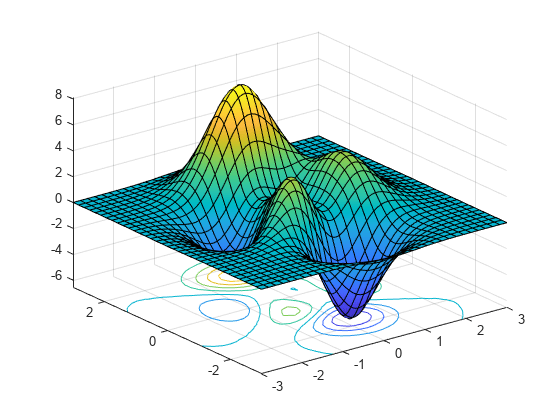
fsurf(f,xyinterval) は、指定された区間にプロットします。x と y の両方で同じ区間を使用するには、[min max] の形式をもつ 2 要素ベクトルとして xyinterval を指定します。異なる区間を使用するには、[xmin xmax ymin ymax] の形式をもつ 4 要素ベクトルを指定します。

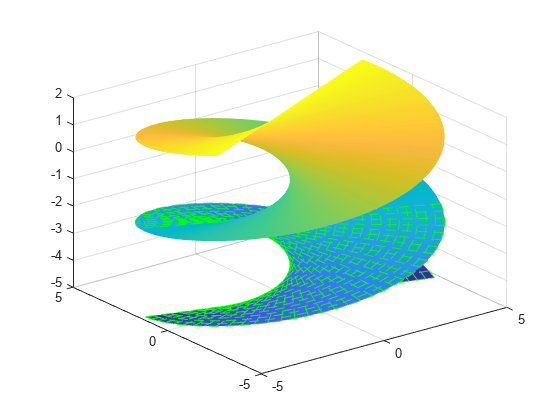
fsurf(funx,funy,funz) は、u と v の既定の区間 [-5 5] に、x = funx(u,v)、y = funy(u,v) および z = funz(u,v) で定義されたパラメトリックな表面をプロットします。

fsurf(funx,funy,funz,uvinterval) は、指定された区間にプロットします。u と v の両方で同じ区間を使用するには、[min max] の形式をもつ 2 要素ベクトルとして uvinterval を指定します。異なる区間を使用するには、[umin umax vmin vmax] の形式をもつ 4 要素ベクトルを指定します。

fsurf(___,LineSpec) は、ライン スタイル、マーカー記号および表面の色を設定します。たとえば、'-r' は赤のラインを指定します。このオプションは、前述した任意の入力引数の組み合わせの後に使用します。

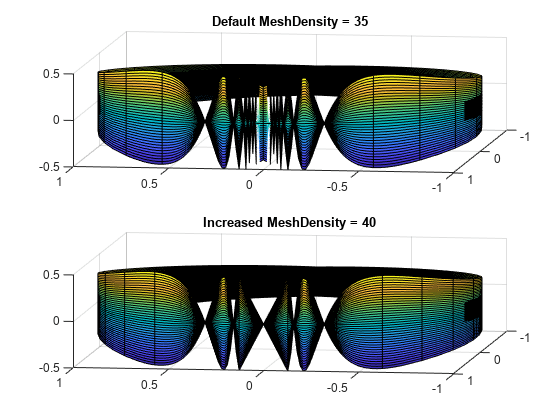
fsurf(___,Name,Value) は、1 つ以上の名前と値のペアの引数を使用して、表面のプロパティを指定します。このオプションは、前述の構文における任意の入力引数が組み合わされてから使用します。

fsurf(ax,___) は、現在の座標軸 (gca) ではなく ax で指定される座標軸にプロットします。

fs = fsurf(___) は、入力に応じて FunctionSurface オブジェクトまたは ParameterizedFunctionSurface オブジェクトを返します。特定の表面のプロパティについてクエリや変更を行うには、fs を使用します。プロパティの一覧については、FunctionSurface のプロパティ または ParameterizedFunctionSurface のプロパティ を参照してください。

例

式の 3 次元表面プロット

既定の区間 $$-5<x<5$$ および $$-5<y<5$$ に式 $$\sin (x)+\cos (y)$$ をプロットします。

fsurf(@(x,y) sin(x)+cos(y))

表面プロットの区間を指定して区分的な式をプロット

区分的な式

$$\begin{array}{cc}erf(x)+\cos (y)& -5<x<0\\ \sin (x)+\cos (y)& 0<x<5\end{array}$$

を $$-5<y<5.$$ にプロットします。

プロット区間を fsurf の 2 番目の入力引数として指定します。同じ座標軸の異なる区間に複数の表面をプロットする場合、すべてのデータが含まれるように軸の範囲が調整されます。

f1 = @(x,y) erf(x)+cos(y);
fsurf(f1,[-5 0 -5 5])
hold on
f2 = @(x,y) sin(x)+cos(y);
fsurf(f2,[0 5 -5 5])
hold off

パラメーター化された表面プロット

パラメーター化された表面

$$\begin{array}{c}x=r\cos (u)\sin (v)\\ y=r\sin (u)\sin (v)\\ z=r\cos (v)\\ wherer=2+\sin (7u+5v)\end{array}$$

を $$0<u<2\pi$$ かつ $$0<v<\pi$$ についてテストします。camlight を使用して表面にライトを追加します。

r = @(u,v) 2 + sin(7.*u + 5.*v);
funx = @(u,v) r(u,v).*cos(u).*sin(v);
funy = @(u,v) r(u,v).*sin(u).*sin(v);
funz = @(u,v) r(u,v).*cos(v);
fsurf(funx,funy,funz,[0 2*pi 0 pi]) 
camlight

タイトルと軸ラベルを追加して目盛りの書式を設定

$$x$$ と $$y$$ について $$-2\pi$$ から $$2\pi$$ まで、3 次元表面 $$y\sin (x)-x\cos (y)$$ をプロットします。タイトルおよび軸ラベルを追加し、座標軸の外枠を表示します。

fsurf(@(x,y) y.*sin(x)-x.*cos(y),[-2*pi 2*pi])
title('ysin(x) - xcos(y) for x and y in [-2\pi,2\pi]')
xlabel('x');
ylabel('y');
zlabel('z');
box on

axes オブジェクトの XTickLabel プロパティと XTick プロパティを使用して、x 軸の目盛り値および関連するラベルを設定します。gca を使用して axes オブジェクトにアクセスします。同様に、y 軸の目盛り値および対応するラベルを設定します。

ax = gca;
ax.XTick = -2*pi:pi/2:2*pi;
ax.XTickLabel = {'-2\pi','-3\pi/2','-\pi','-\pi/2','0',...
    '\pi/2','\pi','3\pi/2','2\pi'};

ax.YTick = -2*pi:pi/2:2*pi;
ax.YTickLabel = {'-2\pi','-3\pi/2','-\pi','-\pi/2','0',...
    '\pi/2','\pi','3\pi/2','2\pi'};

表面のプロパティの指定

異なる $$v$$ 値に異なるライン スタイルを使用して、パラメトリックな表面 $$x=u\sin (v)$$、$$y=-u\cos (v)$$、$$z=v$$ をプロットします。$$-5<v<-2$$ では、表面のエッジに緑の破線を使用します。$$-2<v<2$$ では、EdgeColor プロパティを 'none' に設定してエッジをオフにします。

funx = @(u,v) u.*sin(v);
funy = @(u,v) -u.*cos(v);
funz = @(u,v) v;

fsurf(funx,funy,funz,[-5 5 -5 -2],'--','EdgeColor','g')
hold on
fsurf(funx,funy,funz,[-5 5 -2 2],'EdgeColor','none')
hold off

作成後に表面を変更

次のパラメトリックな表面をプロットします。

$$\begin{array}{c}x=e^{-|u|/10}\sin (5|v|)\\ y=e^{-|u|/10}\cos (5|v|)\\ z=u.\end{array}$$

パラメーター化された関数 surface オブジェクトを変数に割り当てます。

x = @(u,v) exp(-abs(u)/10).*sin(5*abs(v));
y = @(u,v) exp(-abs(u)/10).*cos(5*abs(v));
z = @(u,v) u;
fs = fsurf(x,y,z)

fs = 
  ParameterizedFunctionSurface with properties:

    XFunction: @(u,v)exp(-abs(u)/10).*sin(5*abs(v))
    YFunction: @(u,v)exp(-abs(u)/10).*cos(5*abs(v))
    ZFunction: @(u,v)u
    EdgeColor: [0 0 0]
    LineStyle: '-'
    FaceColor: 'interp'

  Use GET to show all properties

オブジェクトの URange プロパティを設定して、u のプロット区間を [-30 30] に変更します。FaceAlpha プロパティを 0 (透明) から 1 (不透明) の間の値に設定して、表面に透明度を加えます。

fs.URange = [-30 30];
fs.FaceAlpha = .5;

表面プロットの下に等高線を表示

'ShowContours' オプションを 'on' に設定して、表面プロットの下に等高線を表示します。

f = @(x,y) 3*(1-x).^2.*exp(-(x.^2)-(y+1).^2)...
    - 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2)...
    - 1/3*exp(-(x+1).^2 - y.^2);
fsurf(f,[-3 3],'ShowContours','on')

表面プロットの解像度を制御

'MeshDensity' オプションを使用して、表面プロットの解像度を制御します。'MeshDensity' を大きくするとより滑らかで正確なプロットが得られますが、この値を小さくするとプロットの速度が上がります。

タイル表示チャート レイアウトで 2 つのプロットを作成します。最初のプロットで、パラメトリックな表面 $$x=\sin (s)$$、$$y=\cos (s)$$、$$z=(t/10)\sin (1/s)$$ を表示します。表面には大きな隙間があります。2 番目のプロットでは 'MeshDensity' を 40 に増加して、この問題を修正します。fsurf が隙間を埋め、'MeshDensity' の増加によって解像度が上がったことが示されます。

tiledlayout(2,1)
nexttile
fsurf(@(s,t) sin(s), @(s,t) cos(s), @(s,t) t/10.*sin(1./s))
view(-172,25)
title('Default MeshDensity = 35')

nexttile
fsurf(@(s,t) sin(s), @(s,t) cos(s),...
    @(s,t) t/10.*sin(1./s),'MeshDensity',40)

view(-172,25)
title('Increased MeshDensity = 40')

入力引数

f — プロット対象の 3 次元関数

関数ハンドル

プロット対象の 3 次元関数。名前付き関数または無名関数の関数ハンドルとして指定します。

z = f(x,y) の形式の関数を指定します。関数は 2 つの行列の入力引数を受け入れ、同じサイズの行列の出力引数を 1 つ返さなければなりません。最高のパフォーマンスを得るには、行列演算子ではなく、配列演算子を使用します。たとえば、* (mtimes) ではなく .* (times) を使用します。

例: f = @(x,y) sin(x) + cos(y);

xyinterval — x および y のプロット区間

[-5 5 -5 5] (既定値) | [min max] 形式のベクトル | [xmin xmax ymin ymax] 形式のベクトル

x および y のプロット区間。次のいずれかの形式で指定します。

• [min max] 形式のベクトル — x および y の両方に区間 [min max] を使用します。

• [xmin xmax ymin ymax] 形式のベクトル — x に区間 [xmin xmax]、y に区間 [ymin ymax] を使用します。

funx — x 座標のパラメトリック関数

関数ハンドル

x 座標のパラメトリック関数。名前付き関数または無名関数の関数ハンドルとして指定します。

x = funx(u,v) の形式の関数を指定します。関数は 2 つの行列の入力引数を受け入れ、同じサイズの行列の出力引数を 1 つ返さなければなりません。最高のパフォーマンスを得るには、行列演算子ではなく、配列演算子を使用します。たとえば、* (mtimes) ではなく .* (times) を使用します。

例: funx = @(u,v) u.*sin(v);

funy — y 座標のパラメトリック関数

関数ハンドル

y 座標のパラメトリック関数。名前付き関数または無名関数の関数ハンドルとして指定します。

y = funy(u,v) の形式の関数を指定します。関数は 2 つの行列の入力引数を受け入れ、同じサイズの行列の出力引数を 1 つ返さなければなりません。最高のパフォーマンスを得るには、行列演算子ではなく、配列演算子を使用します。たとえば、* (mtimes) ではなく .* (times) を使用します。

例: funy = @(t) @(u,v) -u.*cos(v);

funz — z 座標のパラメトリック関数

関数ハンドル

z 座標のパラメトリック関数。名前付き関数または無名関数の関数ハンドルとして指定します。

z = funz(u,v) の形式の関数を指定します。関数は 2 つの行列の入力引数を受け入れ、同じサイズの行列の出力引数を 1 つ返さなければなりません。最高のパフォーマンスを得るには、行列演算子ではなく、配列演算子を使用します。たとえば、* (mtimes) ではなく .* (times) を使用します。

例: funz = @(u,v) v;

uvinterval — u および v のプロット区間

[-5 5 -5 5] (既定値) | [min max] 形式のベクトル | [umin umax vmin vmax] 形式のベクトル

u および v のプロット区間。次のいずれかの形式で指定します。

• [min max] 形式のベクトル — u および v の両方に区間 [min max] を使用します。

• [umin umax vmin vmax] 形式のベクトル — u に区間 [umin umax]、v に区間 [vmin vmax] を使用します。

ax — axes オブジェクト

axes オブジェクト

axes オブジェクト。axes オブジェクトを指定しない場合、fsurf は現在の座標軸を使用します。

LineSpec — ライン スタイル、マーカー、色

string スカラー | 文字ベクトル

ライン スタイル、マーカー、および色。記号を含む string スカラーまたは文字ベクトルとして指定します。記号の順番は任意です。3 つの特性 (ライン スタイル、マーカーおよび色) をすべて指定する必要はありません。たとえば、ライン スタイルを省略してマーカーを指定する場合、プロットはラインなしでマーカーのみを表示します。

例: "--or" は円形マーカー付きの赤い破線です。

ライン スタイル	説明	結果として得られる線
"-"	実線
"--"	破線
":"	点線
"-."	一点鎖線

マーカー	説明	結果のマーカー
"o"	円
"+"	プラス記号
"*"	アスタリスク
"."	点
"x"	十字
"_"	水平線
"|"	垂直線
"square"	正方形
"diamond"	菱形
"^"	上向き三角形
"v"	下向き三角形
">"	右向き三角形
"<"	左向き三角形
"pentagram"	星形五角形
"hexagram"	星形六角形

色名	省略名	RGB 3 成分	外観
"red"	"r"	[1 0 0]
"green"	"g"	[0 1 0]
"blue"	"b"	[0 0 1]
"cyan"	"c"	[0 1 1]
"magenta"	"m"	[1 0 1]
"yellow"	"y"	[1 1 0]
"black"	"k"	[0 0 0]
"white"	"w"	[1 1 1]

名前と値の引数

引数のオプションのペアを Name1=Value1,...,NameN=ValueN として指定します。ここで Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後になければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、コンマを使用してそれぞれの名前と値を区切り、Name を引用符で囲みます。

例: 'Marker','o','MarkerFaceColor','red'

ここでは、プロパティの一部だけを紹介しています。完全な一覧については、FunctionSurface のプロパティ または ParameterizedFunctionSurface のプロパティ を参照してください。

MeshDensity — 方向ごとの評価点の数

35 (既定値) | 数値

方向ごとの評価点の数。数値として指定します。既定値は 35 です。fsurf オブジェクトでは適応評価を使用するため、評価点の実際の数はそれより多くなります。

例: 100

ShowContours — プロットの下に等高線図を表示

'off' (既定値) | on/off logical 値

プロットの下への等高線図の表示。'on' または 'off'、もしくは数値または logical 1 (true) または 0 (false) として指定します。'on' の値は true と等価であり、'off' は false と等価です。したがって、このプロパティの値を logical 値として使用できます。値は matlab.lang.OnOffSwitchState 型の on/off logical 値として格納されます。

EdgeColor — ラインの色

[0 0 0] (既定値) | 'interp' | RGB 3 成分 | 16 進数カラー コード | 'r' | 'g' | 'b' | ...

ラインの色。'interp'、RGB 3 成分、16 進数カラー コード、色名、または省略名として指定します。既定の RGB 3 成分の値 [0 0 0] は、黒に相当します。'interp' 値では、ZData の値に基づいてエッジに着色します。

カスタム色を使用する場合は、RGB 3 成分または 16 進数カラー コードを指定します。

• RGB 3 成分は、色の赤、緑、青成分の強度を指定する 3 成分の行ベクトルです。強度値は [0,1] の範囲でなければなりません。たとえば [0.4 0.6 0.7] のようになります。

• 16 進数カラー コードは、ハッシュ記号 (#) で始まり、3 桁または 6 桁の 0 から F までの範囲の 16 進数が続く string スカラーまたは文字ベクトルです。この値は大文字と小文字を区別しません。したがって、カラー コード "#FF8800"、"#ff8800"、"#F80"、および "#f80" は等価です。

あるいは、名前を使用して一部の一般的な色を指定できます。次の表に、名前の付いた色オプション、等価の RGB 3 成分、および 16 進数カラー コードを示します。

色名	省略名	RGB 3 成分	16 進数カラー コード	外観
"red"	"r"	[1 0 0]	"#FF0000"
"green"	"g"	[0 1 0]	"#00FF00"
"blue"	"b"	[0 0 1]	"#0000FF"
"cyan"	"c"	[0 1 1]	"#00FFFF"
"magenta"	"m"	[1 0 1]	"#FF00FF"
"yellow"	"y"	[1 1 0]	"#FFFF00"
"black"	"k"	[0 0 0]	"#000000"
"white"	"w"	[1 1 1]	"#FFFFFF"
"none"	該当なし	該当なし	該当なし	色なし

MATLAB^® の多くのタイプのプロットで使用されている既定の色の RGB 3 成分および 16 進数カラー コードを次に示します。

RGB 3 成分	16 進数カラー コード	外観
[0 0.4470 0.7410]	"#0072BD"
[0.8500 0.3250 0.0980]	"#D95319"
[0.9290 0.6940 0.1250]	"#EDB120"
[0.4940 0.1840 0.5560]	"#7E2F8E"
[0.4660 0.6740 0.1880]	"#77AC30"
[0.3010 0.7450 0.9330]	"#4DBEEE"
[0.6350 0.0780 0.1840]	"#A2142F"

LineStyle — ライン スタイル

"-" (既定値) | "--" | ":" | "-." | "none"

ライン スタイル。次の表にリストされたオプションのいずれかとして指定します。

ライン スタイル	説明	結果として得られる線
"-"	実線
"--"	破線
":"	点線
"-."	一点鎖線
"none"	ラインなし	ラインなし

LineWidth — ライン幅

0.5 (既定値) | 正の値

ライン幅。ポイント単位の正の値として指定します。1 ポイントは 1/72 インチです。ラインがマーカーをもつ場合、ライン幅はマーカー エッジにも影響します。

ライン幅をピクセルの幅より細くすることはできません。システムでライン幅をピクセルの幅より細い値に設定すると、ラインは 1 ピクセル幅で表示されます。

Marker — マーカー記号

"none" (既定値) | "o" | "+" | "*" | "." | ...

マーカー記号。次の表に挙げる値のいずれかとして指定します。既定では、オブジェクトはマーカーを表示しません。マーカー記号を指定すると、各データ点または各頂点にマーカーが追加されます。

マーカー	説明	結果のマーカー
"o"	円
"+"	プラス記号
"*"	アスタリスク
"."	点
"x"	十字
"_"	水平線
"|"	垂直線
"square"	正方形
"diamond"	菱形
"^"	上向き三角形
"v"	下向き三角形
">"	右向き三角形
"<"	左向き三角形
"pentagram"	星形五角形
"hexagram"	星形六角形
"none"	マーカーなし	該当なし

MarkerSize — マーカー サイズ

6 (既定値) | 正の値

マーカー サイズ。ポイント単位の正の値として指定します。1 ポイントは 1/72 インチです。

出力引数

fs — 1 つ以上の FunctionSurface オブジェクトまたは ParameterizedFunctionSurface オブジェクト

スカラー | ベクトル

1 つ以上の FunctionSurface オブジェクトまたは ParameterizedFunctionSurface オブジェクト。スカラーまたはベクトルとして返されます。

• fsurf(f) の構文、あるいはこの構文の変形を使用した場合、fsurf は FunctionSurface オブジェクトを返します。

• fsurf(funx,funy,funz) の構文、あるいはこの構文の変形を使用した場合、fsurf は ParameterizedFunctionSurface オブジェクトを返します。

これらのオブジェクトは、特定表面のプロパティのクエリと変更に使用できます。プロパティの一覧については、FunctionSurface のプロパティ および ParameterizedFunctionSurface のプロパティ を参照してください。

バージョン履歴

R2016a で導入

参考

関数

• fcontour | fmesh | fplot | fplot3 | title | hold | fimplicit3

プロパティ

• FunctionSurface のプロパティ | ParameterizedFunctionSurface のプロパティ