ロマプリータ地震の解析
この例では、タイムスタンプ付きの地震データを timetable に保存する方法と、timetable 関数を使用してデータを解析し可視化する方法を説明します。
地震データの読み込み
この例のファイル quake.mat には、1989 年 10 月 17 日、Santa Cruz 山脈で発生したロマプリータ (Loma Prieta) 地震の 200 Hz のデータが含まれています。このデータは、Santa Cruz の California 大学、Charles F. Richter 地震学研究所の Joel Yellin 氏から提供されています。
データの読み込みから始めます。
load quake whos e n v
Name Size Bytes Class Attributes e 10001x1 80008 double n 10001x1 80008 double v 10001x1 80008 double
ワークスペースには、UC Santa Cruz の自然科学棟にある加速度計で記録された時間波形を含む 3 つの変数があります。加速度計は、地震波の本震の振幅を記録しました。変数 n、e、v は、断層に平行に配置され、その N 方向が Sacramento の方向を示す機器で測定された 3 つの方向成分を参照します。データは、機器の応答に対する補正はされていません。
他のベクトルと同じ長さをもつ、200Hz でサンプリングされたタイムスタンプを含む変数 Time を作成します。関数 seconds と乗算によって正しい単位を表し、Hz () のサンプリング レートを得ます。この結果が、経過時間を表すのに役立つ変数durationになります。
Time = (1/200)*seconds(1:length(e))';
whos TimeName Size Bytes Class Attributes Time 10001x1 80010 duration
timetable でのデータの編成
個々の変数をtableやtimetableに整理するとさらに便利です。timetable には、タイムスタンプ付きデータを操作するための柔軟性と機能が備わっています。時間変数および 3 つの加速度変数を使用して timetable を作成し、より意味のある変数名を指定します。関数 head を使用して最初の 8 行を表示します。
varNames = ["EastWest","NorthSouth","Vertical"]; quakeData = timetable(Time,e,n,v,VariableNames=varNames)
quakeData=10001×3 timetable
Time EastWest NorthSouth Vertical
_________ ________ __________ ________
0.005 sec 5 3 0
0.01 sec 5 3 0
0.015 sec 5 2 0
0.02 sec 5 2 0
0.025 sec 5 2 0
0.03 sec 5 2 0
0.035 sec 5 1 0
0.04 sec 5 1 0
0.045 sec 5 1 0
0.05 sec 5 0 0
0.055 sec 5 0 0
0.06 sec 5 0 0
0.065 sec 5 0 0
0.07 sec 5 0 0
0.075 sec 5 0 0
0.08 sec 5 0 0
⋮
ドット表記を使用して timetable の変数にアクセスし、データを調べます。(ドット表記の詳細については、table 内のデータへのアクセスを参照してください。)East-West の振幅を選択し、それを持続時間の関数としてプロット (plot) します。
plot(quakeData.Time,quakeData.EastWest)
title("East-West Acceleration")
データのスケーリング
重力加速度でデータをスケーリングします。つまり、テーブル内の各変数に定数を乗じます。変数はすべて同じ型 (double) であるため、次元名 Variables を使用してすべての変数にアクセスできます。quakeData.Variables を使用すると timetable 内の数値を直接変更できることに注目してください。
quakeData.Variables = 0.098*quakeData.Variables;
調査対象のデータのサブセットの選択
衝撃波の振幅がゼロ近くから最大レベルまで増加し始める時間領域を調べます。上記のプロットを見ると、8 秒から 15 秒までの時間区間が該当の時間であることがわかります。より見やすくなるよう、選択した時点に黒い線を引いてこの区間を目立たせます。後のすべての計算にこの区間が関わってきます。
t1 = seconds(8); t2 = seconds(15); xline(t1,LineWidth=2) xline(t2,LineWidth=2)

対象データの保存
この区間のデータを使用して別の timetable を作成します。対象の行を選択するには、timerangeを使用します。
tr = timerange(t1,t2); quakeData8to15 = quakeData(tr,:)
quakeData8to15=1400×3 timetable
Time EastWest NorthSouth Vertical
_________ ________ __________ ________
8 sec -0.098 2.254 5.88
8.005 sec 0 2.254 3.332
8.01 sec -2.058 2.352 -0.392
8.015 sec -4.018 2.352 -4.116
8.02 sec -6.076 2.45 -7.742
8.025 sec -8.036 2.548 -11.466
8.03 sec -10.094 2.548 -9.8
8.035 sec -8.232 2.646 -8.134
8.04 sec -6.37 2.646 -6.566
8.045 sec -4.508 2.744 -4.9
8.05 sec -2.646 2.842 -3.234
8.055 sec -0.784 2.842 -1.568
8.06 sec 1.078 2.548 0.098
8.065 sec 2.94 2.254 1.764
8.07 sec 4.802 1.96 3.43
8.075 sec 6.664 1.666 4.998
⋮
3 つの加速度変数を異なる 3 つの座標軸で可視化します。3 つのプロットを 3 行 1 列のタイル配置で含むタイル レイアウトを作成するには、tiledlayout関数を使用します。
tiledlayout(3,1) % Tile 1 nexttile plot(quakeData8to15.Time,quakeData8to15.EastWest) ylabel("East-West") title("Acceleration") % tile 2 nexttile plot(quakeData8to15.Time,quakeData8to15.NorthSouth) ylabel("North-South") % Tile 3 nexttile plot(quakeData8to15.Time,quakeData8to15.Vertical) ylabel("Vertical")

要約統計量の計算
データに関する統計情報を表示するには、関数summaryを使用します。
summary(quakeData8to15)
quakeData8to15: 1400×3 timetable
Row Times:
Time: duration
Variables:
EastWest: double
NorthSouth: double
Vertical: double
Statistics for applicable variables and row times:
NumMissing Min Median Max Mean Std
Time 0 8 sec 11.498 sec 14.995 sec 11.498 sec 2.0214 sec
EastWest 0 -255.0940 -0.0980 244.5100 0.9338 66.1188
NorthSouth 0 -198.5480 1.0780 204.3300 -0.1028 42.7980
Vertical 0 -157.8780 0.9800 134.4560 -0.5254 35.8554
データに関する追加の統計情報は、varfunを使用して計算できます。これは、table 内または timetable 内の各変数に関数を適用する際に役立ちます。適用する関数は varfun に関数ハンドルとして渡されます。関数 mean を 3 つの変数すべてに適用し、結果を table 形式で出力します。これは、時間平均を計算した後では時間に意味がなくなるためです。
mn = varfun(@mean,quakeData8to15,OutputFormat="table")mn=1×3 table
mean_EastWest mean_NorthSouth mean_Vertical
_____________ _______________ _____________
0.9338 -0.10276 -0.52542
速度と位置の計算
衝撃波の伝播速度を特定するために、加速度を 1 回積分します。時間変数に沿った累積和を使用して、波面の速度を計算します。
edot = (1/200)*cumsum(quakeData8to15.EastWest); edot = edot - mean(edot);
次に、3 つすべての変数の積分を実行して速度を計算します。関数を作成し、varfun を使用してその関数を timetable 内の変数に適用すると便利です。この例では、その関数が例の最後に velFun という名前で含められています。
vel = varfun(@velFun,quakeData8to15)
vel=1400×3 timetable
Time velFun_EastWest velFun_NorthSouth velFun_Vertical
_________ _______________ _________________ _______________
8 sec -0.56831 0.44642 1.8173
8.005 sec -0.56831 0.45769 1.834
8.01 sec -0.5786 0.46945 1.832
8.015 sec -0.59869 0.48121 1.8114
8.02 sec -0.62907 0.49346 1.7727
8.025 sec -0.66925 0.5062 1.7154
8.03 sec -0.71972 0.51894 1.6664
8.035 sec -0.76088 0.53217 1.6257
8.04 sec -0.79273 0.5454 1.5929
8.045 sec -0.81527 0.55912 1.5684
8.05 sec -0.8285 0.57333 1.5522
8.055 sec -0.83242 0.58754 1.5444
8.06 sec -0.82703 0.60028 1.5449
8.065 sec -0.81233 0.61155 1.5537
8.07 sec -0.78832 0.62135 1.5708
8.075 sec -0.755 0.62968 1.5958
⋮
同じ関数 velFun を速度に適用して位置を特定します。
pos = varfun(@velFun,vel)
pos=1400×3 timetable
Time velFun_velFun_EastWest velFun_velFun_NorthSouth velFun_velFun_Vertical
_________ ______________________ ________________________ ______________________
8 sec 2.1189 -2.1793 -3.0821
8.005 sec 2.1161 -2.177 -3.0729
8.01 sec 2.1132 -2.1746 -3.0638
8.015 sec 2.1102 -2.1722 -3.0547
8.02 sec 2.107 -2.1698 -3.0458
8.025 sec 2.1037 -2.1672 -3.0373
8.03 sec 2.1001 -2.1646 -3.0289
8.035 sec 2.0963 -2.162 -3.0208
8.04 sec 2.0923 -2.1592 -3.0128
8.045 sec 2.0883 -2.1564 -3.005
8.05 sec 2.0841 -2.1536 -2.9972
8.055 sec 2.08 -2.1506 -2.9895
8.06 sec 2.0758 -2.1476 -2.9818
8.065 sec 2.0718 -2.1446 -2.974
8.07 sec 2.0678 -2.1415 -2.9662
8.075 sec 2.064 -2.1383 -2.9582
⋮
varfun で作成された timetable の変数名に、使用した関数の名前が含まれているのがわかります。これは元のデータで実行された操作を追跡するのに役立ちます。ドット表記を使用して変数名を元の値に合わせます。
pos.Properties.VariableNames = varNames; vel.Properties.VariableNames = varNames;
対象とする時間区間における速度と位置の 3 成分をプロットします。速度と位置を 2 行 1 列のタイル配置でプロットします。
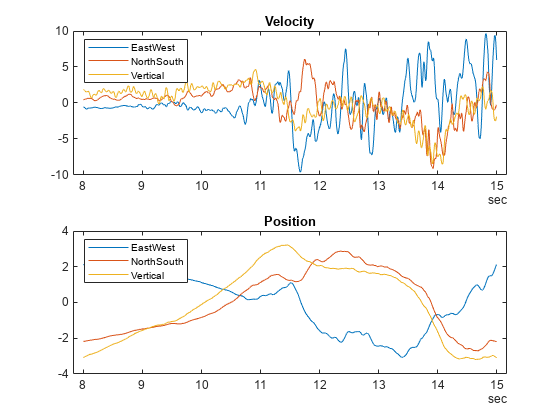
tiledlayout(2,1) % Tile 1 nexttile plot(vel.Time,vel.Variables) legend(vel.Properties.VariableNames,Location="bestoutside") title("Velocity") % Tile 2 nexttile plot(pos.Time,pos.Variables) title("Position")
軌跡の可視化
軌跡は成分値を使用して 2 次元または 3 次元でプロットできます。このプロットは、このデータを可視化する異なった方法を示しています。
最初は 2 次元の写像です。これは 1 つ目で、いくつかの時間値の注釈が付けられています。
figure plot(pos.NorthSouth,pos.Vertical) xlabel("North-South") ylabel("Vertical") % Select locations and label nt = ceil((max(pos.Time) - min(pos.Time))/6); idx = find(fix(pos.Time/nt) == (pos.Time/nt))'; text(pos.NorthSouth(idx),pos.Vertical(idx),char(pos.Time(idx)))

plotmatrixを使用して、すべての変数の散布図を並べ、各変数のヒストグラムを対角線上に配したグリッドを可視化します。出力変数 Ax はグリッドの各座標軸を表し、xlabel と ylabel を使用してラベル付けする座標軸を識別するために使用できます。
figure [S,Ax] = plotmatrix(pos.Variables); for ii = 1:length(varNames) xlabel(Ax(end,ii),varNames{ii}) ylabel(Ax(ii,1),varNames{ii}) end

軌跡の 3 次元表示をプロットし、10 位置点ごとに垂直線をプロットします。垂直線間の間隔は、速度を表します。
step = 10; figure plot3(pos.NorthSouth,pos.EastWest,pos.Vertical,"r") hold on plot3(pos.NorthSouth(1:step:end),pos.EastWest(1:step:end),pos.Vertical(1:step:end),"|") hold off box axis tight xlabel("North-South") ylabel("East-West") zlabel("Vertical") title("Position")

サポート関数
関数は以下のように定義されます。
function y = velFun(x) y = (1/200)*cumsum(x); y = y - mean(y); end
参考
timetable | head | summary | varfun | duration | seconds | timerange