このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

obliqueslice

3 次元ボリューム データからの斜体スライスの抽出

R2020a 以降

構文

B = obliqueslice(V,point,normal)

B = obliqueslice(V,point,normal,Name=Value)

[B,x,y,z] = obliqueslice(___)

説明

B = obliqueslice(V,point,normal) は、2 次元斜体スライスを 3 次元ボリューム データ V から抽出します。スライスは、ボリューム上の指定された点への参照と法線ベクトルと共に抽出されます。スライス平面は法線ベクトルに対して垂直であり、指定された点を通過しています。

指定された点と法線に対してスライスがどのように抽出されるかは、斜体スライスを参照してください。

B = obliqueslice(V,point,normal,Name=Value) は、1 つ以上の名前と値の引数を使用してオプションを指定します。

[B,x,y,z] = obliqueslice(___) は、抽出されたスライスの入力ボリュームにおける 3 次元直交座標も返します。これらの 3 次元座標における強度値がどのように 2 次元平面にマッピングされるかの詳細については、3 次元座標空間からイメージ平面への値のマッピングを参照してください。

例

3 次元ボリューム データからの斜体スライスの抽出

3 次元ボリューム データ セットをワークスペースに読み込みます。

load mri

関数 squeeze を使用して、大きさが 1 の次元を削除します。

V = squeeze(D);

関数 montage を使用して、データの水平スライスを表示します。

montage(V,map,'Size',[3 9]);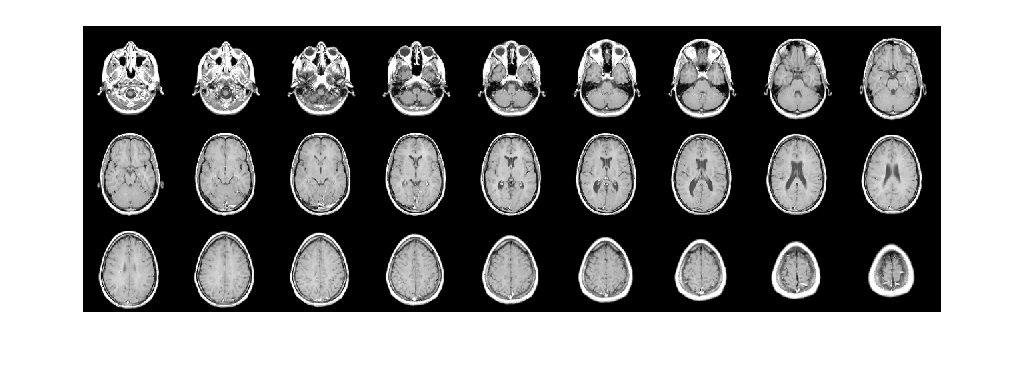

スライスが通過するボリューム内の点を指定します。

point = [73 50 15.5];

3 次元座標空間における法線ベクトルを指定します。

normal = [0 15 20];

ボリューム データからスライスを抽出します。スライスは法線ベクトルに対して垂直であり、指定された点を通過しています。

[B,x,y,z] = obliqueslice(V,point,normal);

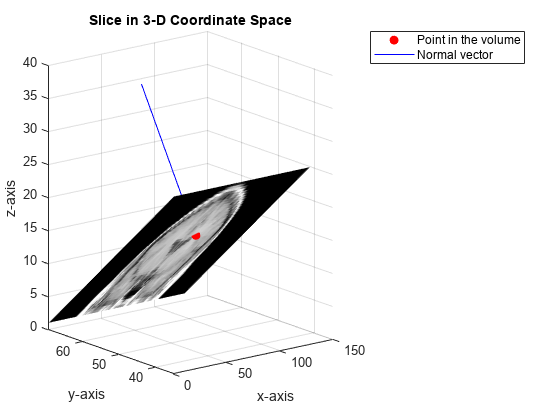
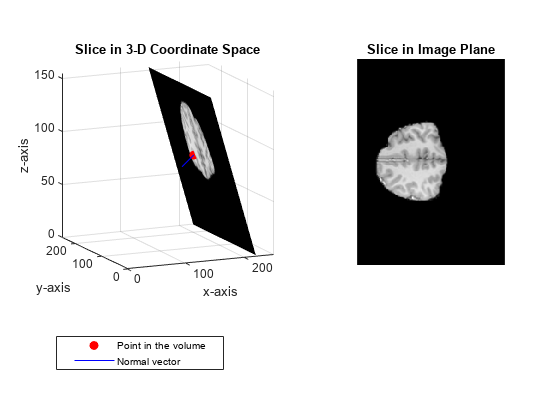
抽出されたスライスを 3 次元座標空間に表示します。

figure
surf(x,y,z,B,'EdgeColor','None','HandleVisibility','off');
grid on
view([-38 12])
colormap(gray)
xlabel('x-axis')
ylabel('y-axis');
zlabel('z-axis');
title('Slice in 3-D Coordinate Space')

点と法線ベクトルをプロットします。

hold on
plot3(point(1),point(2),point(3),'or','MarkerFaceColor','r');
plot3(point(1)+[0 normal(1)],point(2)+[0 normal(2)],point(3)+[0 normal(3)], ...
    '-b','MarkerFaceColor','b');
hold off
legend('Point in the volume','Normal vector')

抽出されたスライスをイメージ平面に表示します。

figure
imshow(B,[])
title('Slice in Image Plane')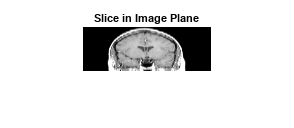

法線ベクトルに沿った複数スライスの抽出

3 次元ボリューム データ セットをワークスペースに読み込みます。

s = load(fullfile(toolboxdir('images'),'imdata','BrainMRILabeled','images','vol_001.mat'));
V = s.vol;

関数 montage を使用して、データの水平スライスを表示します。

montage(V,'Indices',12:118,'Size',[8 12],'DisplayRange',[]);

3 次元座標空間における平面に法線ベクトルを指定します。

normal = [20 0 10];

for ループを使用して、法線ベクトルの方向に沿って複数のスライスを抽出します。それぞれの反復で次を行います。

• スライスが通過する点を指定します。

• 出力サイズを 'Full' に設定し、パディングするピクセルの塗りつぶしの値を 255 に設定して、スライスを抽出します。抽出されたスライスは法線ベクトルに対して垂直であり、指定された点を通過しています。

• 抽出されたスライスを表示します。

sliceIdx = 10:5:180;

figure
for s = 1:length(sliceIdx)
    
    pt = [sliceIdx(s) 150 80];
    [B,x,y,z] = obliqueslice(V,pt,normal,'OutputSize','Full','FillValues',255);

    Bslices(:,:,s) = B;

    % Display the slice in 3-D coordinate space
    subplot('Position',[0.11 0.36 0.38 0.5])
    surf(x,y,z,B,'EdgeColor','None','HandleVisibility','off');
    grid on
    view([-24 12])
    colormap(gray)
    xlabel('x-axis')
    ylabel('y-axis');
    zlabel('z-axis');
    zlim([0 155]);
    ylim([0 250]);
    xlim([0 250]);
    title('Slice in 3-D Coordinate Space') 
    % Plot the point and the normal vector.
    hold on
    plot3(pt(1),pt(2),pt(3),'or','MarkerFaceColor','r')
    plot3( ...
        pt(1)+[-normal(1) normal(1)], ...
        pt(2)+[-normal(2) normal(2)], ...
        pt(3)+[-normal(3) normal(3)], ...
        '-b','MarkerFaceColor','b')
    legend('Point in the volume','Normal vector','Position',[0.1 0.12 0.3 0.08])
    hold off   
    % Display the extracted slice.
    subplot('Position',[0.6 0.37 0.34 0.49])
    imshow(B,[])
    title('Slice in Image Plane')
    pause(0.5);  
end    

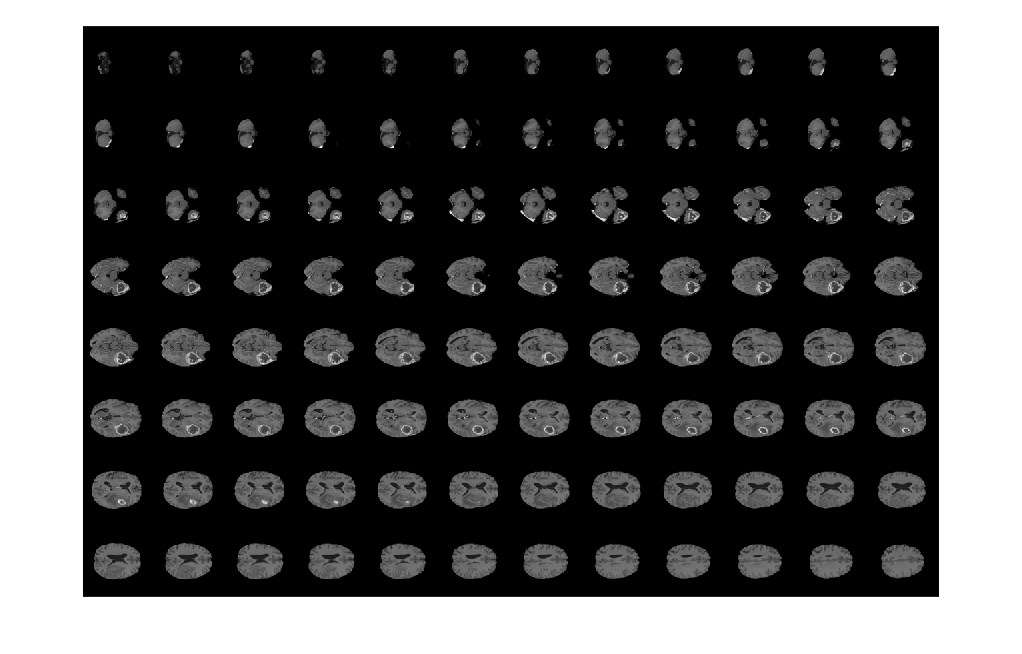
関数 montage を使用して、抽出されたイメージ スライスを表示します。

figure
montage(Bslices,'Size',[5 7],'DisplayRange',[]);

入力引数

V — 入力ボリューム

3 次元数値配列 | 3 次元 categorical 配列

入力ボリューム。3 次元の数値配列または 3 次元の categorical 配列として指定します。

データ型: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | logical | categorical

point — ボリューム内の点

3 要素の行ベクトル

ボリューム内の点。[p_x p_y p_z] の形式の 3 要素行ベクトルとして指定します。

データ型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

normal — 法線ベクトル

3 要素の行ベクトル

法線ベクトル。[a b c] 形式の 3 要素行ベクトルとして指定します。法線ベクトルとは、表面または平面に垂直なベクトルのことです。

直交スライスを抽出するには、法線ベクトルを次のいずれかの値に設定します。

• [1 0 0] — yz 平面のスライスを抽出します。

• [0 1 0] — xz 平面のスライスを抽出します。

• [0 0 1] — xy 平面のスライスを抽出します。

データ型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

例: obliqueslice(V,point,normal,OutputSize="Full")

R2021a より前では、コンマを使用して名前と値をそれぞれ区切り、Name を引用符で囲みます。

例: obliqueslice(V,point,normal,"OutputSize","Full")

Method — 内挿法

"linear" | "nearest"

内挿法。次のいずれかの値として指定します。

• "linear" — 線形内挿

• "nearest" — 最近傍内挿

V が数値の場合、内挿法の既定の設定は "linear" ですが、"nearest" として指定することもできます。V が categorical の場合、内挿法は "nearest" でなければなりません。

データ型: char | string

OuputSize — 出力イメージのサイズ

"limit" (既定値) | "full"

出力イメージのサイズ。次のいずれかの値として指定します。

• "limit" — 出力イメージのサイズは、入力ボリュームの次元に対する 2 次元スライスの実際のサイズになります。抽出されたスライス領域が正方形または四角形でない場合、この関数は抽出されたスライス領域にピクセルを付加して自動的にパディングし、正方形または長方形のイメージにします。

• "full" — 出力イメージのサイズは、2 次元スライスの実際のサイズと等しくならない場合があります。出力イメージのサイズは、法線ベクトル normal において入力ボリュームから取得可能な最大スライス サイズに設定されます。イメージのサイズを変更するため、抽出された 2 次元スライスの境界に行および列が付加されてパディングされます。

  パディングされたピクセルの塗りつぶしの値は、既定では 0 です。名前と値の引数 FillValues を使用して、この値を変更できます。

データ型: char | string

FillValues — パディングされたピクセルの塗りつぶしの値

0 (既定値) | 数値スカラー | 文字ベクトル | missing

パディングされたピクセルの塗りつぶしの値。数値スカラー、文字ベクトル、または missing として指定します。

V が数値配列の場合は、次のように指定します。

• ゼロ パディングをする場合、0。

• 定数パディングをする場合、数値スカラー。

V が categorical 配列の場合は、次のように指定します。

• 入力データのカテゴリを示す文字ベクトル。カテゴリを確認するには、関数 categories を使用します。

• 入力データのカテゴリが <undefined> と等しい場合は、missing。

データ型: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | char

出力引数

B — 出力 2 次元スライス

数値行列 | categorical 行列

出力 2 次元スライス。数値行列または categorical 行列として返されます。出力スライスのデータ型は、入力ボリュームのデータ型と同じになります。

データ型: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | logical | categorical

x — 出力スライスの x 座標

数値行列

3 次元ボリュームにおける出力スライスの x 座標。出力スライス B と同じサイズの数値行列として返されます。

データ型: single

y — 出力スライスの y 座標

数値行列

3 次元ボリュームにおける出力スライスの y 座標。出力スライス B と同じサイズの数値行列として返されます。

データ型: single

z — 出力スライスの z 座標

数値行列

3 次元ボリュームにおける出力スライスの z 座標。出力スライス B と同じサイズの数値行列として返されます。

データ型: single

詳細

斜体スライス

指定された点 (p_x, p_y, p_z) と法線ベクトル (a, b, c) に従い、この関数は平面の方程式 a(x-p_x)+b(y-p_y)+c(z-p_z) = 0 を解きます。

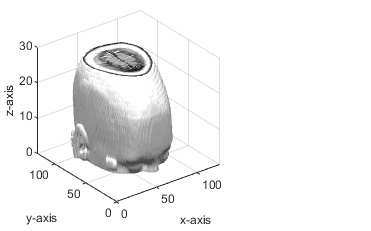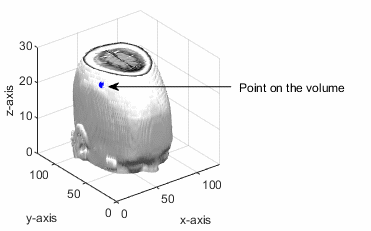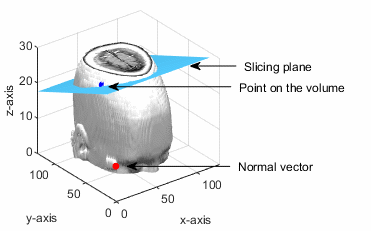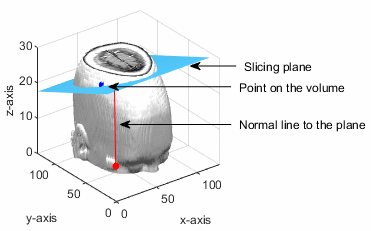
点 (p_x, p_y, p_z) はボリューム データ内にあります。スライス平面は法線ベクトルに対して垂直であり、指定された点を通過しています。

3 次元座標空間からイメージ平面への値のマッピング

抽出されたスライスの 3 次元空間における座標がどのような順序で 2 次元平面にマッピングされるかは、水平面と垂直面に対する傾斜角に依存します。

関数 obliqueslice は、イメージ スライスを構成する点の 3 次元座標空間における x、y、および z 座標を含む出力行列 x、y、および z を返します。関数 obliqueslice は、これらの点における強度値を内挿し、その値を 2 次元平面にマッピングします。出力行列の最初の値 x(1,1), y(1,1), z(1,1) は、イメージ平面の左上隅のピクセル (1, 1) としてマッピングされる点の 3 次元座標を指定します。イメージ スライスを構成する 3 次元座標およびそれらに関連付けられた強度値は、この点を起点として、左から右、上から下のスキャン順序で読み取られます。これらの強度値は、左から右、上から下の同じスキャン順序で 2 次元イメージ平面を埋めます。

V を入力ボリューム データ、B を 2 次元出力イメージとすると、B(i,j) = V(a,b,c) となります。

ここで、a = x(i,j)、b = y(i,j)、および c = z(i,j) です。

拡張機能

スレッドベースの環境

MATLAB® の backgroundPool を使用してバックグラウンドでコードを実行するか、Parallel Computing Toolbox™ の ThreadPool を使用してコードを高速化します。

この関数は、スレッドベースの環境を完全にサポートします。詳細については、スレッドベースの環境での MATLAB 関数の実行を参照してください。

バージョン履歴

R2020a で導入

R2022b: スレッドベース環境のサポート

obliqueslice は、スレッドベースの環境をサポートするようになりました。

参考

関数

• slice

オブジェクト

• sliceViewer | orthosliceViewer | volshow