深層学習を使用したイメージ処理演算子の近似
この例では、マルチスケール コンテキスト集約ネットワーク (CAN) を使用してイメージ フィルター処理を近似する方法を説明します。
演算子の近似は、従来のイメージ処理演算またはイメージ処理パイプラインからの出力と結果が類似するイメージ処理のために、代替方法を見つけます。多くの場合、演算子の近似の目的は、1 つのイメージの処理に必要な時間を短縮することです。
複数の従来の手法および深層学習の手法が、演算子の近似を実行するために提案されています。いくつかの従来の手法は単一のアルゴリズムの効率を改善しますが、他の演算に対して一般化できません。別の一般的な手法として、1 つのイメージの低解像度のコピーに演算子を適用することで、広範囲な演算を近似します。ただし、高周波数成分が失われるため、近似の精度が制限されます。
深層学習ソリューションでは、より一般的で複雑な演算の近似が可能です。たとえば、Q. Chen [1] によるマルチスケール コンテキスト集約ネットワーク (CAN) では、マルチスケール トーン マッピング、写真スタイル変換、非ローカルのかすみ低減、鉛筆描画を近似できます。マルチスケール CAN はフル解像度のイメージで学習を行うため、より高い精度で高周波数成分を処理できます。ネットワークの学習を行うと、ネットワークが従来の処理演算をバイパスしてイメージを直接処理できるようになります。
この例では、バイラテラル イメージ フィルター処理を近似するようにマルチスケール CAN に学習させて、エッジの鮮鋭度を維持しながらイメージのノイズを低減する方法を説明します。この例は、学習データストアの作成、学習オプションの選択、ネットワークの学習、ネットワークを使用したテスト イメージの処理を含む、学習と推論の包括的なワークフローを示します。

演算子の近似ネットワーク
マルチスケール CAN は、イメージ処理演算の従来の出力と、マルチスケール コンテキスト集約を使用して入力イメージを処理した後のネットワーク応答との間の 損失を最小限に抑えるように学習させています。マルチスケール コンテキスト集約は、各ピクセルに関する情報をイメージ全体から検出し、ピクセル周囲の小さな近傍の検索対象に限定しません。
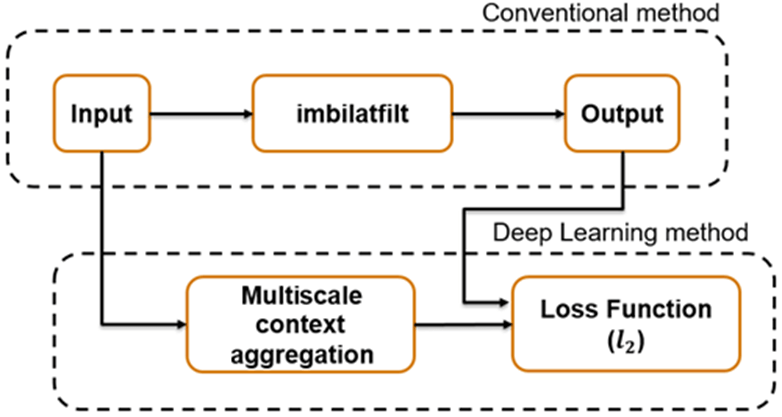
ネットワークがグローバルなイメージ プロパティを学習できるように、マルチスケール CAN アーキテクチャには大規模な受容野があります。演算子によってイメージのサイズが変更されてはならないため、最初と最後の層のサイズは同じになります。倍率が指数的に増加することで、連続する中間層が膨張します (そのため、CAN は "マルチスケール" な性質を持ちます)。膨張によってネットワークは、イメージの解像度を低下させることなく、さまざまな空間周波数で空間的に分離された特徴を検出できます。ネットワークは、各畳み込み層の後に適応型の正規化を使用して、バッチ正規化の影響と近似された演算子に対する恒等写像のバランスを調整します。
学習データのダウンロード
20,000 個の静止した自然イメージから成る、IAPR TC-12 ベンチマークをダウンロードします [2]。このデータ セットには、人物、動物、都市などの写真が含まれます。データ ファイルのサイズは~1.8 GB です。ネットワークに学習させるのに必要な学習データ セットをダウンロードしない場合、コマンド ラインで load("trainedBilateralFilterNet_v2.mat"); を入力して、事前学習済みの CAN を読み込むことができます。それから、この例のマルチスケール CAN を使用したバイラテラル フィルター処理の近似の実行の節に進みます。
データをダウンロードするために補助関数 downloadIAPRTC12Data を使用します。この関数は、この例にサポート ファイルとして添付されています。dataDir をデータの目的の場所として指定します。
dataDir =  tempdir;
downloadIAPRTC12Data(dataDir);
tempdir;
downloadIAPRTC12Data(dataDir);Downloading IAPR TC-12 dataset... This will take several minutes to download and unzip... Done.
この例ではネットワークを IAPRTC-12 ベンチマーク データの小さなサブセットで学習させます。
trainImagesDir = fullfile(dataDir,"iaprtc12","images","39"); exts = [".jpg",".bmp",".png"]; pristineImages = imageDatastore(trainImagesDir,FileExtensions=exts);
学習イメージの数を表示します。
numel(pristineImages.Files)
ans = 916
学習データの準備
学習データ セットを作成するには、初期状態のイメージを読み取り、バイラテラル フィルター処理が行われたイメージを書き出します。フィルター処理されたイメージは、ディスク内の preprocessDataDir で指定されたディレクトリに格納されます。
preprocessDataDir = fullfile(trainImagesDir,"preprocessedDataset");補助関数 bilateralFilterDataset を使用して学習データを前処理します。この関数は、この例にサポート ファイルとして添付されています。この補助関数は、inputImages の初期状態の各イメージに対して以下の操作を実行します。
バイラテラル フィルター処理の平滑化の度合いを計算します。フィルター処理されたイメージを平滑化すると、イメージのノイズが低減されます。
imbilatfiltを使用してバイラテラル フィルター処理を実行します。imwriteを使用して、フィルター処理されたイメージをディスクに保存します。
bilateralFilterDataset(pristineImages,preprocessDataDir);
学習用ランダム パッチ抽出データストアの定義
ランダム パッチ抽出データストアを使用して、ネットワークに学習データを供給します。このデータストアは、ネットワーク入力と目的のネットワーク応答が含まれる 2 つのイメージ データストアから、対応するランダムなパッチを抽出します。
この例では、ネットワーク入力は pristineImages の初期状態のイメージです。目的のネットワーク応答は、バイラテラル フィルター処理後のイメージです。バイラテラル フィルター処理が行われたイメージ ファイルのコレクションから bilatFilteredImages という名前のイメージ データストアを作成します。
bilatFilteredImages = imageDatastore(preprocessDataDir,FileExtensions=exts);
2 つのイメージ データストアから randomPatchExtractionDatastore を作成します。パッチ サイズとして 256 x 256 ピクセルを指定します。学習時に、ランダムに配置されたパッチをイメージの各ペアから 1 つずつ抽出するため、名前と値の引数 PatchesPerImage を指定します。ミニバッチ サイズとして 1 を指定します。
miniBatchSize = 1;
patchSize = [256 256];
dsTrain = randomPatchExtractionDatastore(pristineImages,bilatFilteredImages, ...
patchSize,PatchesPerImage=1);
dsTrain.MiniBatchSize = miniBatchSize;randomPatchExtractionDatastore ではデータのミニバッチが、エポックの各反復でネットワークに渡されます。データを調査するためにデータストアで読み取り操作を実行します。
inputBatch = read(dsTrain); disp(inputBatch)
InputImage ResponseImage
_________________ _________________
{256×256×3 uint8} {256×256×3 uint8}
マルチスケール CAN 層のセットアップ
この例では、Deep Learning Toolbox™ の以下を含む層を使用してマルチスケール CAN を定義します。
imageInputLayer(Deep Learning Toolbox) — イメージ入力層convolution2dLayer(Deep Learning Toolbox) — 畳み込みニューラル ネットワーク用の 2 次元畳み込み層batchNormalizationLayer(Deep Learning Toolbox) — バッチ正規化層leakyReluLayer(Deep Learning Toolbox) — 漏洩正規化線形ユニット層
適応型のバッチ正規化層を実装するために 2 つのカスタム スケール層が追加されます。これらの層はサポート ファイルとしてこの例に付加されます。
adaptiveNormalizationMu— バッチ正規化分岐の強度を調整するスケール層adaptiveNormalizationLambda— 恒等分岐の強度を調整するスケール層
第 1 層 imageInputLayer はイメージ パッチに対して作用します。パッチ サイズは、ネットワークの最上位層の応答に影響する空間イメージ領域であるネットワーク受容野に基づきます。イメージ内の高レベルの特徴をすべて確認できるように、ネットワーク受容野のサイズはイメージのサイズと同じであるのが理想的です。バイラテラル フィルターの場合、近似イメージのパッチ サイズは 256 x 256 に固定されます。
networkDepth = 10; numberOfFilters = 32; firstLayer = imageInputLayer([256 256 3],Name="InputLayer",Normalization="none");
イメージ入力層に続いて、サイズが 3 行 3 列の 32 個のフィルターがある 2 次元畳み込み層があります。畳み込みを行うたびに、特徴マップのサイズが入力サイズと同じになるように、各畳み込み層の入力をゼロ パディングします。重みを初期化して単位行列にします。
Wgts = zeros(3,3,3,numberOfFilters); for ii = 1:3 Wgts(2,2,ii,ii) = 1; end convolutionLayer = convolution2dLayer(3,numberOfFilters,Padding=1, ... Weights=Wgts,Name="Conv1");
各畳み込み層の後に、バッチ正規化層、およびバッチ正規化分岐の強度を調整する適応型の正規化スケール層が続きます。後にこの例では、恒等分岐の強度を調整する、対応する適応型の正規化スケール層を作成します。ここでは、adaptiveNormalizationMu 層の後に 1 つの加算層が続きます。最後に、負の入力のスカラー乗数が 0.2 の leaky ReLU 層を指定します。
batchNorm = batchNormalizationLayer(Name="BN1"); adaptiveMu = adaptiveNormalizationMu(numberOfFilters,"Mu1"); addLayer = additionLayer(2,Name="add1"); leakyrelLayer = leakyReluLayer(0.2,Name="Leaky1");
同じパターンに従ってネットワークの中間層を指定します。連続する畳み込み層には、ネットワークの深さによって指数的にスケーリングする膨張係数があります。
midLayers = [convolutionLayer batchNorm adaptiveMu addLayer leakyrelLayer];
Wgts = zeros(3,3,numberOfFilters,numberOfFilters);
for ii = 1:numberOfFilters
Wgts(2,2,ii,ii) = 1;
end
for layerNumber = 2:networkDepth-2
dilationFactor = 2^(layerNumber-1);
padding = dilationFactor;
conv2dLayer = convolution2dLayer(3,numberOfFilters, ...
Padding=padding,DilationFactor=dilationFactor, ...
Weights=Wgts,Name="Conv"+num2str(layerNumber));
batchNorm = batchNormalizationLayer(Name="BN"+num2str(layerNumber));
adaptiveMu = adaptiveNormalizationMu(numberOfFilters,"Mu"+num2str(layerNumber));
addLayer = additionLayer(2,Name="add"+num2str(layerNumber));
leakyrelLayer = leakyReluLayer(0.2,Name="Leaky"+num2str(layerNumber));
midLayers = [midLayers conv2dLayer batchNorm adaptiveMu addLayer leakyrelLayer];
end最後から 2 番目の畳み込み層には膨張係数を適用しないでください。
conv2dLayer = convolution2dLayer(3,numberOfFilters, ... Padding=1,Weights=Wgts,Name="Conv9"); batchNorm = batchNormalizationLayer(Name="AN9"); adaptiveMu = adaptiveNormalizationMu(numberOfFilters,"Mu9"); addLayer = additionLayer(2,Name="add9"); leakyrelLayer = leakyReluLayer(0.2,Name="Leaky9"); midLayers = [midLayers conv2dLayer batchNorm adaptiveMu addLayer leakyrelLayer];
最後の畳み込み層は、イメージを再構成するサイズ 1 x 1 x 32 x 3 の単一のフィルターを備えています。
Wgts = sqrt(2/(9*numberOfFilters))*randn(1,1,numberOfFilters,3); finalLayer = convolution2dLayer(1,3,NumChannels=numberOfFilters, ... Weights=Wgts,Name="Conv10");
すべての層を連結します。
layers = [firstLayer midLayers finalLayer];
空の dlnetwork オブジェクトを作成し、そのオブジェクトに層を追加します。
opNet = dlnetwork; opNet = addLayers(opNet,layers);
適応型の正規化方程式の恒等分岐として機能するスキップ接続を作成します。スキップ接続を加算層に結合します。
skipConv1 = adaptiveNormalizationLambda(numberOfFilters,"Lambda1"); skipConv2 = adaptiveNormalizationLambda(numberOfFilters,"Lambda2"); skipConv3 = adaptiveNormalizationLambda(numberOfFilters,"Lambda3"); skipConv4 = adaptiveNormalizationLambda(numberOfFilters,"Lambda4"); skipConv5 = adaptiveNormalizationLambda(numberOfFilters,"Lambda5"); skipConv6 = adaptiveNormalizationLambda(numberOfFilters,"Lambda6"); skipConv7 = adaptiveNormalizationLambda(numberOfFilters,"Lambda7"); skipConv8 = adaptiveNormalizationLambda(numberOfFilters,"Lambda8"); skipConv9 = adaptiveNormalizationLambda(numberOfFilters,"Lambda9"); opNet = addLayers(opNet,skipConv1); opNet = connectLayers(opNet,"Conv1","Lambda1"); opNet = connectLayers(opNet,"Lambda1","add1/in2"); opNet = addLayers(opNet,skipConv2); opNet = connectLayers(opNet,"Conv2","Lambda2"); opNet = connectLayers(opNet,"Lambda2","add2/in2"); opNet = addLayers(opNet,skipConv3); opNet = connectLayers(opNet,"Conv3","Lambda3"); opNet = connectLayers(opNet,"Lambda3","add3/in2"); opNet = addLayers(opNet,skipConv4); opNet = connectLayers(opNet,"Conv4","Lambda4"); opNet = connectLayers(opNet,"Lambda4","add4/in2"); opNet = addLayers(opNet,skipConv5); opNet = connectLayers(opNet,"Conv5","Lambda5"); opNet = connectLayers(opNet,"Lambda5","add5/in2"); opNet = addLayers(opNet,skipConv6); opNet = connectLayers(opNet,"Conv6","Lambda6"); opNet = connectLayers(opNet,"Lambda6","add6/in2"); opNet = addLayers(opNet,skipConv7); opNet = connectLayers(opNet,"Conv7","Lambda7"); opNet = connectLayers(opNet,"Lambda7","add7/in2"); opNet = addLayers(opNet,skipConv8); opNet = connectLayers(opNet,"Conv8","Lambda8"); opNet = connectLayers(opNet,"Lambda8","add8/in2"); opNet = addLayers(opNet,skipConv9); opNet = connectLayers(opNet,"Conv9","Lambda9"); opNet = connectLayers(opNet,"Lambda9","add9/in2");
サンプル入力イメージを使用して dlnetwork オブジェクトを初期化します。
opNet = initialize(opNet,dlarray(single(inputBatch.InputImage{1}),"SSCB"));ディープ ネットワーク デザイナー (Deep Learning Toolbox)アプリを使用して、ネットワークを可視化します。
deepNetworkDesigner(opNet)
学習オプションの指定
Adam オプティマイザーを使用してネットワークに学習させます。関数trainingOptions (Deep Learning Toolbox)を使用してハイパーパラメーター設定を指定します。"Momentum" の既定値 0.9、および "L2Regularization" (重み減衰) の既定値 0.0001 を使用します。一定の学習率 0.0001 を指定します。学習を 181 エポック行います。
maxEpochs = 181; initLearningRate = 0.0001; miniBatchSize = 1; options = trainingOptions("adam", ... InitialLearnRate=initLearningRate, ... MaxEpochs=maxEpochs, ... MiniBatchSize=miniBatchSize, ... Plots="training-progress", ... Verbose=false);
ネットワークの学習
この例では既定で、バイラテラル フィルターを近似するように事前学習させたマルチスケール CAN を読み込みます。この事前学習済みのネットワークを使用することで、学習の完了を待たずにバイラテラル フィルターの近似を実行できます。
ネットワークに学習させるには、次のコードで変数 doTraining を true に設定します。関数trainnet (Deep Learning Toolbox)を使用してニューラル ネットワークに学習させます。回帰の場合は、平均二乗誤差損失を使用します。既定では、関数 trainnet は利用可能な GPU がある場合にそれを使用します。GPU での学習には、Parallel Computing Toolbox™ ライセンスとサポートされている GPU デバイスが必要です。サポートされているデバイスの詳細については、GPU 計算の要件 (Parallel Computing Toolbox)を参照してください。そうでない場合、関数 trainnet は CPU を使用します。実行環境を指定するには、ExecutionEnvironment 学習オプションを使用します。学習には NVIDIA® Titan X GPU で約 15 時間を要します。
doTraining =false; if doTraining net = trainnet(dsTrain,opNet,"mean-squared-error",options); modelDateTime = string(datetime("now",Format="yyyy-MM-dd-HH-mm-ss")); save("trainedBilateralFilterNet_v2-"+modelDateTime+".mat","net"); else load("trainedBilateralFilterNet_v2.mat"); end
マルチスケール CAN を使用したバイラテラル フィルター処理の近似の実行
バイラテラル フィルターを近似する学習済みのマルチスケール CAN ネットワークを使用してイメージを処理するには、この例の残りの手順を実行します。この例の残りでは、次の処理を実行する方法を示します。
参照イメージからノイズを含む入力イメージのサンプルを作成します。
関数
imbilatfiltを使用してノイズを含むイメージの従来のバイラテラル フィルター処理を実行します。CAN を使用してノイズを含むイメージのバイラテラル フィルター処理に対する近似を実行します。
演算子の近似と従来のバイラテラル フィルター処理によるノイズ除去後のイメージを視覚的に比較します。
ノイズ除去後のイメージと初期状態の参照イメージとの類似度を定量化することで、ノイズ除去後のイメージの画質を評価します。
ノイズを含むサンプル イメージの作成
演算子の近似と従来のバイラテラル フィルター処理の結果の比較に使用する、ノイズを含むサンプル イメージを作成します。
テスト データ セット testImages には、Image Processing Toolbox™ に付属する 20 個の歪みのないイメージが含まれています。イメージを imageDatastore に読み込み、そのイメージをモンタージュに表示します。
fileNames = ["sherlock.jpg","peacock.jpg","fabric.png","greens.jpg", ... "hands1.jpg","kobi.png","lighthouse.png","office_4.jpg", ... "onion.png","pears.png","yellowlily.jpg","indiancorn.jpg", ... "flamingos.jpg","sevilla.jpg","llama.jpg","parkavenue.jpg", ... "strawberries.jpg","trailer.jpg","wagon.jpg","football.jpg"]; filePath = fullfile(matlabroot,"toolbox","images","imdata")+filesep; filePathNames = strcat(filePath,fileNames); testImages = imageDatastore(filePathNames);
テスト イメージをモンタージュとして表示します。
montage(testImages)

バイラテラル フィルター処理の参照イメージとして使用するイメージを 1 つ選択します。イメージをデータ型 uint8 に変換します。
testImage =  "fabric.png";
Ireference = imread(testImage);
Ireference = im2uint8(Ireference);
"fabric.png";
Ireference = imread(testImage);
Ireference = im2uint8(Ireference);独自のイメージを参照イメージとして使用することもできます。テスト イメージのサイズは 256 行 256 列以上でなければなりません。テスト イメージが 256 行 256 列より小さい場合、関数imresizeを使用してイメージのサイズを大きくします。ネットワークには RGB テスト イメージも必要です。テスト イメージがグレースケールの場合、関数 cat を使用してイメージを RGB に変換し、3 番目の次元に沿って、元のイメージの 3 つのコピーを連結します。
参照イメージを表示します。
imshow(Ireference)
title("Pristine Reference Image")
関数 imnoise を使用して、分散 0.00001 のゼロ平均のガウス ホワイト ノイズを参照イメージに追加します。
Inoisy = imnoise(Ireference,"gaussian",0.00001); imshow(Inoisy) title("Noisy Image")

バイラテラル フィルター処理を使用したイメージのフィルター処理
従来のバイラテラル フィルター処理は、エッジの鮮鋭度を維持したままイメージのノイズを除去する標準的な方法です。ノイズを含むイメージにバイラテラル フィルターを適用するには、関数 imbilatfilt を使用します。平滑化の度合いをピクセル値の分散に等しくなるように指定します。
degreeOfSmoothing = var(double(Inoisy(:)));
Ibilat = imbilatfilt(Inoisy,degreeOfSmoothing);
imshow(Ibilat)
title("Denoised Image Obtained Using Bilateral Filtering")
学習済みネットワークを使用したイメージの処理
正規化された入力イメージを学習済みネットワークに渡し、出力を観測します。ネットワークの出力は目的のノイズ除去後のイメージとなり、dlarray オブジェクトとして返されます。関数 extractdata を使用して、dlarray オブジェクトからイメージ データを抽出します。
InoisyDL = dlarray(single(Inoisy),"SSCB");
IapproxDL = predict(net,InoisyDL);
Iapprox = extractdata(IapproxDL);Image Processing Toolbox では、浮動小数点イメージのピクセル値の範囲が [0, 1] である必要があります。関数 rescale を使用してピクセル値がこの範囲になるようにスケーリングし、イメージを uint8 に変換します。
Iapprox = rescale(Iapprox);
Iapprox = im2uint8(Iapprox);
imshow(Iapprox)
title("Denoised Image Obtained Using Multiscale CAN")
視覚的な比較
ノイズ除去後のイメージを視覚的によく把握するために、それぞれのイメージ内の小領域を調べます。関心領域 (ROI) をベクトル roi を使って [x y width height] の形式で指定します。各要素は、ROI の左上隅の x と y 座標、幅と高さで定義されます。
roi = [300 30 50 50];
イメージをこの ROI にトリミングして、結果をモンタージュとして表示します。CAN では従来のバイラテラル フィルター処理より多くのノイズが除去されています。いずれの手法でもエッジの鮮鋭度は維持されています。
montage({imcrop(Ireference,roi),imcrop(Inoisy,roi), ...
imcrop(Ibilat,roi),imcrop(Iapprox,roi)}, ...
Size=[1 4]);
title("Reference Image | Noisy Image | Bilateral-Filtered Image | CAN Prediction");
定量的比較
画質メトリクスを使用して、ノイズを含む入力イメージ、バイラテラル フィルター処理後のイメージ、および演算子の近似が行われたイメージを定量的に比較します。参照イメージは、ノイズを追加する前の元の参照イメージ Ireference です。
参照イメージに対する各イメージのピーク S/N 比 (PSNR) を測定します。PSNR の値が大きいほど、一般には画質が高いことを示します。このメトリクスの詳細については、psnrを参照してください。
noisyPSNR = psnr(Inoisy,Ireference); bilatPSNR = psnr(Ibilat,Ireference); approxPSNR = psnr(Iapprox,Ireference); PSNR_Score = [noisyPSNR bilatPSNR approxPSNR]';
各イメージの構造的類似性 (SSIM) 指数を測定します。SSIM は参照イメージに対してイメージの 3 つの特性である輝度、コントラスト、構造の視覚的影響を評価します。SSIM 値が 1 に近いほど、テスト イメージは参照イメージに近づきます。このメトリクスの詳細については、ssimを参照してください。
noisySSIM = ssim(Inoisy,Ireference); bilatSSIM = ssim(Ibilat,Ireference); approxSSIM = ssim(Iapprox,Ireference); SSIM_Score = [noisySSIM bilatSSIM approxSSIM]';
Naturalness Image Quality Evaluator (NIQE) を使用して、知覚的画質を測定します。NIQE スコアが小さいほど知覚的画質が良好なことを示します。このメトリクスの詳細については、niqeを参照してください。
noisyNIQE = niqe(Inoisy); bilatNIQE = niqe(Ibilat); approxNIQE = niqe(Iapprox); NIQE_Score = [noisyNIQE bilatNIQE approxNIQE]';
メトリクスの表を表示します。
table(PSNR_Score,SSIM_Score,NIQE_Score, ... RowNames=["Noisy Image","Bilateral Filtering","Operator Approximation"])
ans=3×3 table
PSNR_Score SSIM_Score NIQE_Score
__________ __________ __________
Noisy Image 20.276 0.76228 11.574
Bilateral Filtering 25.753 0.91534 6.924
Operator Approximation 26.173 0.92976 5.8165
参考文献
[1] Chen, Q. J. Xu, and V. Koltun. "Fast Image Processing with Fully-Convolutional Networks." In Proceedings of the 2017 IEEE Conference on Computer Vision. Venice, Italy, Oct. 2017, pp. 2516-2525.
[2] Grubinger, M., P. Clough, H. Müller, and T. Deselaers. "The IAPR TC-12 Benchmark: A New Evaluation Resource for Visual Information Systems." Proceedings of the OntoImage 2006 Language Resources For Content-Based Image Retrieval. Genoa, Italy. Vol. 5, May 2006, p. 10.
参考
randomPatchExtractionDatastore | dlnetwork (Deep Learning Toolbox) | trainingOptions (Deep Learning Toolbox) | trainnet (Deep Learning Toolbox) | predict (Deep Learning Toolbox) | imbilatfilt
トピック
- イメージの深層学習向け前処理 (Deep Learning Toolbox)
- 深層学習用のデータストア (Deep Learning Toolbox)
- 深層学習層の一覧 (Deep Learning Toolbox)