ハイパースペクトルイメージ処理入門

ハイパースペクトルイメージングでは、多数の異なる波長においてオブジェクトをイメージ化することにより、そのオブジェクトの空間特性およびスペクトル特性を測定します。波長の範囲は可視スペクトルを超え、紫外線 (UV) から長波長赤外線 (LWIR) の波長までのスペクトルを含みます。最も良く知られているのは可視、近赤外、および中赤外の波長域です。ハイパースペクトルイメージセンサーは、指定されたスペクトル範囲内で連続した狭い波長をもつ複数のイメージを取得します。それぞれのイメージには、さらに微細で詳細な情報が含まれています。さまざまな波長における異なる情報は、次のような多様な用途で役立ちます。

植生、水塊、道路の識別などのリモートセンシング用途 (さまざまな地形は特有のスペクトルシグネチャをもつため)。
果物の成熟度監視などの非破壊検査または外観検査用途。
組織セグメンテーションなどの医用画像用途。

ハイパースペクトルイメージ処理では、ハイパースペクトルイメージに含まれる情報の表現、解析、および解釈を行います。

Hyperspectral image processing workflow

ハイパースペクトルデータの表現

ハイパースペクトルイメージセンサーの測定値は、バンド順データ並び (BSQ)、画素挟み込みバンド並び (BIP)、またはライン挟み込みバンド並び (BIL) の各エンコード形式を使用することによりバイナリデータファイルに格納されます。このデータファイルは、データファイル内の値を正しく表現するために必要なセンサーパラメーター、撮影設定、空間次元、スペクトル波長、エンコード形式などの補助的情報 (メタデータ) を格納するヘッダーファイルに関連付けられています。あるいは、TIFF や NITF ファイル形式の場合、補助的情報をデータファイルに直接追加することもできます。

ハイパースペクトルイメージ処理の場合、データファイルから読み取られた値は 3 次元 (3-D) 配列 (M×N×C) に配置されます。ここで、M および N は取得したデータの空間次元、C は取得中に使用されるスペクトル波長 (バンド) の数を指定する空間次元です。したがって、3 次元配列を、さまざまな波長で取得した一連の 2 次元 (2-D) 単色イメージとして考えることができます。このセットは、"ハイパースペクトルデータキューブ" または "データキューブ" と呼ばれます。

関数 hypercube は、データファイルおよび関連するヘッダーファイル内のメタデータ情報を読み取ることでデータキューブを作成します。関数 hypercube は、hypercube オブジェクトを作成し、そのプロパティにデータキューブ、スペクトル波長、およびメタデータを格納します。hypercube オブジェクトは、Image Processing Toolbox™ Hyperspectral Imaging Library の他のすべての関数に対する入力として使用できます。ハイパースペクトルビューアーアプリを使用すると、ハイパースペクトルイメージを対話的に可視化して処理できます。

大きなハイパースペクトルイメージ

非常に大きな空間解像度のハイパースペクトルイメージを処理するには大量のシステムメモリが必要なため、MATLAB のメモリが不足する可能性があります。大きなハイパースペクトルイメージを小さな関心領域にトリミングし、hypercube オブジェクトとその関数を使用してその小さな領域のみをメモリに読み取ることができます。大きなハイパースペクトルイメージの小さな領域を処理する方法の例については、Process Large Hyperspectral Imagesを参照してください。

データキューブのカラー表現

イメージ化されているオブジェクトを可視化および把握するには、配色を使用してデータキューブを 2 次元イメージとして表現することが有効です。データキューブのカラー表現を使用すると、データを視覚的に検査し、より的確に意思決定を行えるようになります。関数 colorize を使用すると、データキューブの赤-緑-青 (RGB)、フォールスカラー、およびカラー赤外 (CIR) 表現を計算できます。

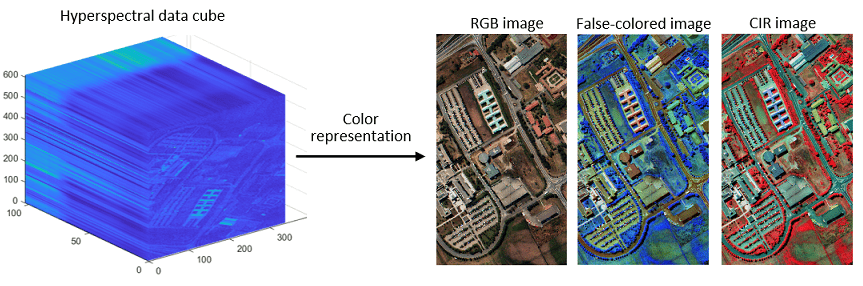
Hyperspectral data cube and colorization

RGB 配色では、赤、緑、および青のスペクトルバンド応答を使用してハイパースペクトルデータキューブの 2 次元イメージを生成します。RGB 配色では自然な外観が得られますが、微細な情報が大幅に失われます。
フォールスカラー配色では、赤、緑、および青の可視スペクトルバンド以外の任意の数のバンドを組み合わせて使用します。フォールスカラー表現を使用すると、可視スペクトル外のバンドのスペクトル応答を可視化できます。フォールスカラー配色は、ハイパースペクトルデータのすべてのスペクトルバンドにわたって特徴的な情報を効率的に取得します。
CIR 配色では NIR 範囲のスペクトルバンドを使用します。ハイパースペクトルデータキューブの CIR 表現は、データキューブの植生範囲を表示および分析する場合に特に有効です。

前処理

ハイパースペクトルイメージングセンサーは、通常、スペクトル分解能が高く、空間分解能が低くなります。取得されたハイパースペクトルデータの空間特性とスペクトル特性は、そのピクセルによって特徴付けられます。各ピクセルは、z 個の異なるバンドにおける場所 (x, y) での強度を示す値のベクトルです。このベクトルは "ピクセルスペクトル" と呼ばれ、(x, y) にあるピクセルのスペクトルシグネチャを定義します。ピクセルスペクトルはハイパースペクトルデータ分析において重要な特徴です。ただし、これらのピクセルスペクトルは、センサーのノイズ、分解能の低さ、大気効果、およびセンサーによるスペクトル歪みなどの要因により歪められます。

Data Cube and Pixel Spectrum

関数 denoiseNGMeet を使用すると、non-local meets global 法を使用してハイパースペクトルデータからノイズを除去できます。

ハイパースペクトルデータの空間分解能を高めるには、イメージフュージョン法を使用します。フュージョン法では、同じシーンに含まれる低分解能のハイパースペクトルデータと高分解能のマルチスペクトルデータ (またはパンクロマチックイメージ) の情報を組み合わせます。この手法は、ハイパースペクトルイメージ分析では "シャープ化" または "パンシャープン" とも呼ばれます。パンシャープンは、特に、ハイパースペクトルデータとパンクロマチックデータのフュージョンを指します。関数 sharpencnmf を使用すると、coupled non-matrix factorization 法を使用してハイパースペクトルデータをシャープ化できます。

大気効果を補正するには、まず、デジタル値 (DN) であるピクセル値をキャリブレーションしなければなりません。ラジオメトリック補正法および大気補正法を使用して DN をキャリブレーションし、データを前処理しなければなりません。この処理ではピクセルスペクトルの解釈が改善され、複数のデータセットを解析する場合に良い結果が得られます。さらに、取得時にハイパースペクトルセンサーの特性によって発生するスペクトル歪みにより、スペクトルシグネチャが不正確になる可能性があります。さらなる解析のためにスペクトルデータの信頼性を高めるには、ハイパースペクトルイメージにおけるスペクトル歪みを大幅に低減する前処理手法を適用しなければなりません。ハイパースペクトルデータの補正方法については、Hyperspectral Data Correctionを参照してください。

どのハイパースペクトルイメージングアプリケーションでも重要となる前処理手順として、その他に "次元削減" があります。ハイパースペクトルデータ内の多くの帯域では、データキューブで処理を行うと計算量が増大します。バンドイメージは連続しているため、帯域にまたがる冗長な情報が存在します。ハイパースペクトルイメージの隣接帯域には高い相関性があるため、スペクトルが冗長になります。バンドイメージを無相関化することにより、冗長なバンドを取り除くことができます。データキューブのスペクトル次元を削減するための一般的な手法としては、帯域選択や直交変換などがあります。

"帯域選択" 法では、直交空間投影を利用して、データキューブ内でスペクトルが特徴的で情報量が最も多い帯域を見つけます。関数 selectBands を使用して情報量が最も多い帯域を見つけ、関数 removeBands を使用して 1 つ以上の帯域を削除します。
主成分分析 (PCA) や最大ノイズフラクション (MNF) などの "直交変換" は、帯域情報を無相関化し、主成分バンドを見つけます。
PCA は、データをより低い次元の空間に変換し、入力帯域の最大分散に沿った方向の主成分ベクトルを見つけます。この主成分は前述の全分散の量の降順で並んでいます。
MNF は、分散ではなく S/N 比を最大にする主成分を計算します。MNF 変換はノイズの多いバンドイメージから主成分を抽出する場合に特に有効です。主成分バンドは、スペクトルが特徴的で帯域間相関が低い帯域です。
関数 hyperpca および hypermnf は、PCA 変換と MNF 変換をそれぞれ使用してデータキューブのスペクトル次元を削減します。削減後のデータキューブから抽出されたピクセルスペクトルを使用して、ハイパースペクトルデータを解析できます。

スペクトルアンミキシング

ハイパースペクトルイメージでは、ピクセルごとに記録された強度値が、そのピクセルが属する領域のスペクトル特性を示しています。この領域は、均一表面となる場合も不均一表面となる場合もあります。均一表面に属するピクセルは "ピュアピクセル" と呼ばれます。こうしたピュアピクセルは、ハイパースペクトルデータの "エンドメンバー" を構成します。

不均一表面は 2 つ以上の異なる均一表面を組み合わせたものです。不均一表面に属するピクセルは "ミクセル" と呼ばれます。ミクセルのスペクトルシグネチャは 2 つ以上のエンドメンバーシグネチャを組み合わせたものです。この空間的な異質性は、主にハイパースペクトルセンサーの空間分解能が低いことによるものです。

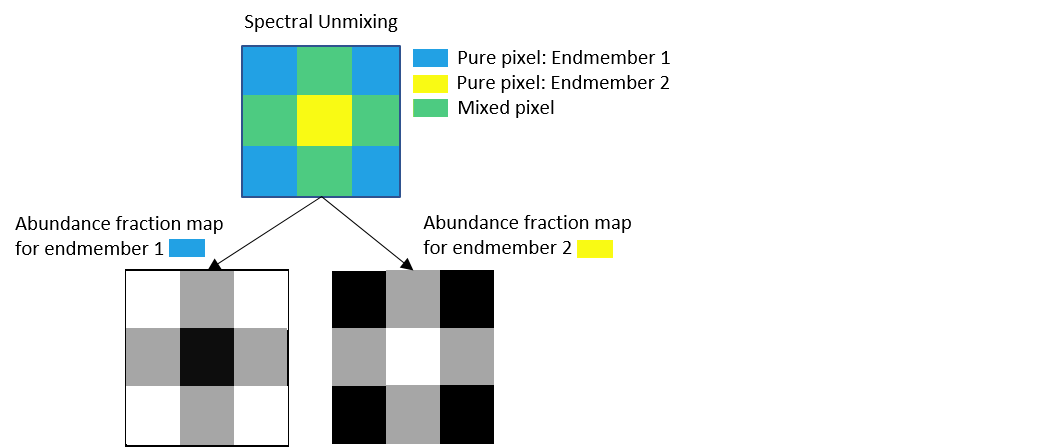
Spectral unmixing

"スペクトルアンミキシング" とは、ミクセルのスペクトルシグネチャをその構成エンドメンバーに分解する処理のことです。スペクトルアンミキシング処理には次の 2 つの手順が含まれます。

"エンドメンバー抽出" — エンドメンバーのスペクトルは、ハイパースペクトルデータの特徴を顕著に表しており、ハイパースペクトルイメージを効果的にスペクトルアンミキシングするために使用できます。効果的なエンドメンバー抽出手法には、Pixel Purity Index (PPI)、Fast Iterative Pixel Purity Index (FIPPI)、N-finder (N-FINDR) などの凸幾何学ベースの手法があります。
- 関数 ppi を使用すると、PPI 法によりエンドメンバーを推定します。PPI 法では、ピクセルスペクトルを直交空間に投影し、投影先空間内の極値ピクセルをエンドメンバーとして識別します。これは非反復手法であり、その結果は直交投影用に生成されたランダム単位ベクトルによって異なります。結果を改善するには投影用のランダム単位ベクトルの数を増やさなければなりませんが、それにより計算量が増える可能性があります。
- 関数 fippi を使用すると、FIPPI 法によりエンドメンバーを推定します。FIPPI 法は反復手法であり、自動ターゲット生成処理を使用して直交投影用の初期の単位ベクトルセットを推定します。このアルゴリズムは PPI 法より収束が速く、他と比べて特徴的なエンドメンバーを識別します。
- 関数 nfindr を使用すると、N-FINDR 法によりエンドメンバーを推定します。N-FINDR は、ピクセルスペクトルを使用することでシンプレックスを構築する反復手法です。この手法は、エンドメンバーにより構成されるシンプレックスのボリュームが、他のピクセルの組み合わせで定義されるボリュームよりも大きいことを前提とします。シンプレックスのボリュームが大きいピクセルシグネチャのセットがエンドメンバーとなります。
"存在量マップの推定" — エンドメンバーのシグネチャが与えられた場合は、各ピクセルに存在するエンドメンバーごとのフラクション量を推定することが有効です。エンドメンバーごとに存在量マップを生成できますが、これはイメージ内のエンドメンバースペクトルの分布を表しています。そのピクセルについて取得したすべての存在量マップ値を比較することで、エンドメンバースペクトルに属するピクセルにラベルを付けることができます。
関数 estimateAbundanceLS を使用して、エンドメンバースペクトルごとの存在量マップを推定します。

スペクトルマッチングとターゲット検出

関数 spectralMatch を使用してスペクトルマッチングを実行するか、関数 detectTarget を使用してターゲット検出を実行して、ピクセルスペクトルを解釈します。"スペクトルマッチング" では、エンドメンバー物質のスペクトルを 1 つ以上の基準スペクトルと比較して、エンドメンバー物質のクラスを同定します。基準データは、スペクトルライブラリとして使用できる物質のピュアスペクトルシグネチャで構成されます。関数 readEcostressSig を使用して、ECOSTRESS スペクトルライブラリから基準スペクトルファイルを読み取ります。その後、関数 spectralMatch を使用して、ECOSTRESS ライブラリスペクトル内のファイルとエンドメンバー物質のスペクトルの類似度を計算できます。

また、スペクトルマッチングを使用して物質を識別したり、"ターゲット検出" を実行して、ターゲットのスペクトルシグネチャがハイパースペクトルイメージ内の他の領域と異なる場合にハイパースペクトルイメージ内の特定のターゲットを検出したりすることもできます。ただし、ターゲット領域と他の領域との間でスペクトルのコントラストが低い場合、スペクトルのマッチングはより困難になります。そのような場合、関数 detectTarget によって提供されるような、より高度なターゲット検出アルゴリズムを使用しなければなりません。これは、ハイパースペクトルデータキューブ全体を考慮し、統計的手法または機械学習手法を使用するものです。スペクトルマッチングおよびターゲット検出手法の詳細については、Spectral Matching and Target Detection Techniquesを参照してください。

スペクトルインデックスとセグメンテーション

"スペクトルインデックス" とは、2 つ以上のスペクトルバンドの比や差などの関数です。スペクトルインデックスは、スペクトル特性に基づいてイメージ内のさまざまな領域を区別して識別します。各ピクセルのスペクトルインデックスを計算することで、ハイパースペクトルデータを、対象の特徴の有無と密度をインデックス値で示したシングルバンドイメージに変換できます。関数 spectralIndices と関数 customSpectralIndex を使用して、ハイパースペクトルイメージ内のさまざまな領域を識別します。スペクトルインデックスの詳細については、Spectral Indicesを参照してください。

スペクトルインデックスは、変化検知やハイパースペクトルイメージのしきい値ベースセグメンテーションにも使用できます。スペクトルインデックスを使用して区別できない領域をセグメント化するには、関数 hyperslic を使用した Simple Linear Iterative Clustering (SLIC) や、関数 hyperseganchor を使用したアンカーグラフといったスペクトルクラスタリング手法を使用できます。

用途

ハイパースペクトルイメージ処理の用途には、土地被覆分類、材料解析、ターゲット検出、変化検知、外観検査、医用画像解析などがあります。

ハイパースペクトルイメージ内の各ピクセルを分類することによる土地被覆の分類。分類の例については、以下の例を参照してください。
スペクトルライブラリを使用したハイパースペクトルイメージ内の材料の識別。例については、スペクトルライブラリを使用したエンドメンバー物質の同定を参照してください。
ターゲット物質の既知のスペクトルシグネチャとハイパースペクトルデータのピクセルスペクトルを照合することによるターゲット検出の実行。ターゲット検出の例については、スペクトルシグネチャマッチングを使用したターゲットの検出およびShip Detection from Sentinel-1 C Band SAR Data Using YOLOX Object Detectionを参照してください。
時間の経過に伴うハイパースペクトルイメージの変化の検知。変化検知の例については、Change Detection in Hyperspectral ImagesおよびMap Flood Areas Using Sentinel-1 SAR Imageryを参照してください。
果物の成熟度監視などの外観検査および非破壊検査作業の実施。ハイパースペクトルイメージの包括的なスペクトルデータにより、正確で非破壊的な解析が可能になります。例については、Predict Sugar Content in Grape Berries Using PLS Regression on Hyperspectral Dataを参照してください。
ハイパースペクトル医用画像の解析。例については、Segment Spleen in Hyperspectral Image of Porcine Tissueを参照してください。