このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

ss2ss

状態空間モデルの状態座標変換

構文

sysT = ss2ss(sys,T)

説明

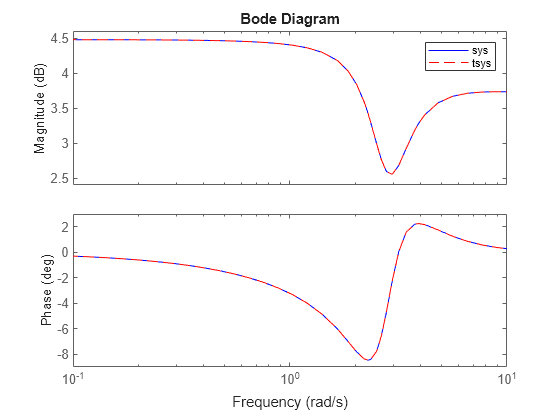
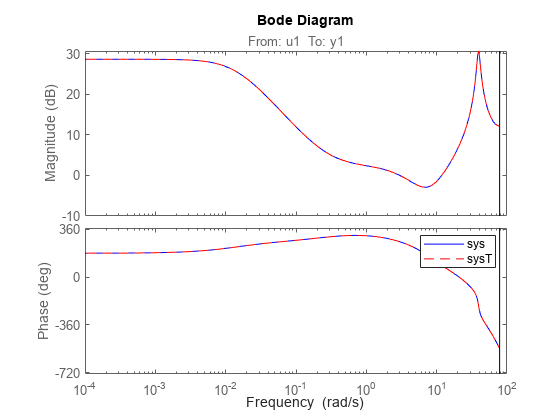
ss2ss は、状態空間モデルの状態ベクトル x に対して相似変換 z = Tx を実行します。詳細については、アルゴリズムを参照してください。

sysT = ss2ss(sys,T) は、指定された変換行列 T を使用して sys の状態座標変換を実行します。行列 T は可逆でなければなりません。

例

状態空間モデルの相似変換

状態空間モデルの相似変換を実行します。

ランダムな状態空間モデルと変換行列を生成します。

rng(0)
sys = rss(5);  
t = randn(5);

変換を実行して、両方のモデルの周波数応答をプロットします。

tsys = ss2ss(sys,t);
bode(sys,'b',tsys,'r--')
legend

両方のモデルの応答が厳密に一致します。

一般化状態空間モデルの相似変換

ss2ss は、状態変換を、一般化モデルの数値部分の状態ベクトルにのみ適用します。

genss モデルを作成します。

sys = rss(2,2,2) * tunableSS('a',2,2,3) + tunableGain('b',2,3)

Generalized continuous-time state-space model with 2 outputs, 3 inputs, 4 states, and the following blocks:
  a: Tunable 2x3 state-space model, 2 states, 1 occurrences.
  b: Tunable 2x3 gain, 1 occurrences.

Type "ss(sys)" to see the current value and "sys.Blocks" to interact with the blocks.

変換行列を指定して、変換を取得します。

T = [1 -2;3 5];
tsys = ss2ss(sys,T)

Generalized continuous-time state-space model with 2 outputs, 3 inputs, 4 states, and the following blocks:
  a: Tunable 2x3 state-space model, 2 states, 1 occurrences.
  b: Tunable 2x3 gain, 1 occurrences.

Type "ss(tsys)" to see the current value and "tsys.Blocks" to interact with the blocks.

両方のモデルを分解します。

[H,B,~,~] = getLFTModel(sys);
[H1,B1,~,~] = getLFTModel(tsys);

分解された sys からのモデルで個別に変換を取得します。

H2 = ss2ss(H,T);

この変換されたモデルを、分解された tsys からのモデルと比較します。

isequal(H1,H2)

ans = logical
   1

両方のモデルは等価です。

同定された状態空間モデルの相似変換

ファイル icEngine.mat には、サンプリング レート 0.04 秒で収集した 1500 の入力/出力サンプルによる 1 つのデータセットが含まれます。入力 u(t) は、By-Pass Idle Air Valve (BPAV) を制御する電圧 (V) で、出力 y(t) は、エンジン速度 (RPM/100) です。

icEngine.mat のデータを使用して、同定可能なパラメーターをもつ状態空間モデルを作成します。

load icEngine.mat
z = iddata(y,u,0.04);
sys = n4sid(z,4,'InputDelay',2);

ランダムな変換行列を指定します。

T = randn(4);

変換を取得します。

sysT = ss2ss(sys,T);

周波数応答を比較します。

bode(sys,'b',sysT,'r--')
legend

応答は厳密に一致します。

複素係数をもつモデルの変換

ss2ss を使用して、複素係数をもつモデルの相似変換も実行できます。

この例では、複素係数をもつランダムな状態空間モデルを生成します。

rng(0)
sys = ss(randn(5)+1i*randn(5),randn(5,3),randn(2,5)+1i*randn(2,5),0,.1);

複素数データを含む変換行列を指定します。

T = randn(5)+1i*randn(5);

変換を取得します。

sysT = ss2ss(sys,T);

周波数応答の特異値を比較します。

sigma(sys,'b',sysT,'r--')
legend

応答は両方の分岐で厳密に一致します。

入力引数

sys — 動的システム

動的システム モデル

動的システム。SISO または MIMO 動的システム モデルとして指定します。使用できる動的システムには次のようなものがあります。

• ss (Control System Toolbox) や dss (Control System Toolbox) モデルなどの連続時間または離散時間の数値 LTI モデル。

• genss (Control System Toolbox) や uss (Robust Control Toolbox) モデルなどの一般化された、あるいは不確かさをもつ LTI モデル。(不確かさをもつモデルを使用するには Robust Control Toolbox™ ソフトウェアが必要です。)

  このようなモデルでは、状態変換は、モデルの数値部分の状態ベクトルにのみ適用されます。これらのモデルの分解の詳細については、getLFTModel (Control System Toolbox) と一般化モデルの内部構造 (Control System Toolbox)を参照してください。

• 同定された状態空間 idss モデル

sys が状態空間モデルの配列である場合、ss2ss は変換 T を配列内の各個別モデルに適用します。

T — 変換行列

行列

変換行列。n 行 n 列の行列として指定します。n は状態の数です。T は、状態空間モデル sys の状態ベクトルと変換後のモデル sysT の状態ベクトル間の変換です (アルゴリズムを参照)。

出力引数

sysT — 変換後のモデル

動的システム モデル

変換後の状態空間モデル。sys と同じタイプの動的システム モデルとして返されます。

アルゴリズム

ss2ss は、状態空間モデルの状態ベクトル x に対して相似変換 $$\overline{x}=Tx$$ を実行します。

各モデル形式について ss2ss で返される変換を次の表にまとめます。

入力モデル	変換後のモデル
次の形式の陽的な状態空間モデル: $$\begin{array}{l}\dot{x}=Ax+Bu\\ y=Cx+Du\end{array}$$	$$\begin{array}{l}\dot{\overline{x}}=TA{T}^{-1}\overline{x}+TBu\\ y=C{T}^{-1}\overline{x}+Du\end{array}$$
次の形式の記述子 (陰的な) 状態空間モデル: $$\begin{array}{c}E\dot{x}=Ax+Bu\\ y=Cx+Du\end{array}$$	$$\begin{array}{c}E{T}^{-1}\dot{\overline{x}}=A{T}^{-1}\overline{x}+Bu\\ y=C{T}^{-1}\overline{x}+Du\end{array}$$
次の形式の同定された状態空間 (idss) モデル: $$\begin{array}{c}\frac{dx}{dt}=Ax+Bu+Ke\\ y=Cx+Du+e\end{array}$$	$$\begin{array}{l}\dot{\overline{x}}=TA{T}^{-}{}^1\overline{x}+TBu+TKe\\ y=C{T}^{-}{}^1\overline{x}+Du+e\end{array}$$

バージョン履歴

R2006a より前に導入

R2021b: ss2ss は、記述子状態空間モデルの異なる変換結果を返します。

記述子状態空間モデルの場合

$$\begin{array}{c}E\dot{x}=Ax+Bu\\ y=Cx+Du,\end{array}$$

ss2ss は以下を返します。

$$\begin{array}{c}E{T}^{-1}\dot{\overline{x}}=A{T}^{-1}\overline{x}+Bu\\ y=C{T}^{-1}\overline{x}+Du.\end{array}$$

以前は、以下の変換が返されていました。

$$\begin{array}{c}TE{T}^{-1}\dot{\overline{x}}=TA{T}^{-1}\overline{x}+TBu\\ y=C{T}^{-1}\overline{x}+Du\end{array}$$

R2021b: mechss モデルでは、相似変換はサポートされなくなりました。

ss2ss ではスパース 2 次 (mechss) モデルはサポートされなくなりました。mechss モデルで相似変換を実行すると、対称性が破棄され、明確な一般形式はありません。

参考

balreal (Control System Toolbox) | canon (Control System Toolbox) | balance

トピック

• 状態空間モデルを最大精度にスケーリング (Control System Toolbox)