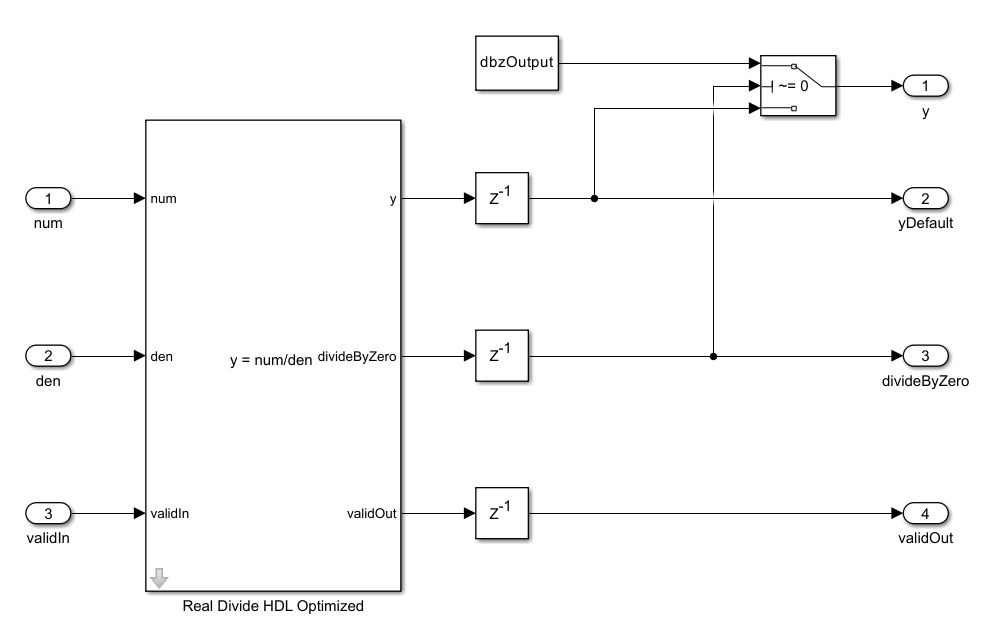
Real Divide HDL Optimized
ライブラリ:
Fixed-Point Designer HDL Support /
Math Operations
説明
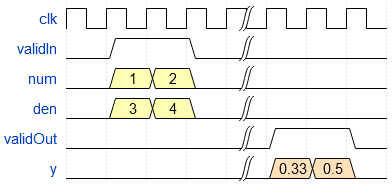
Real Divide HDL Optimized ブロックは、実数スカラー num を実数スカラー den で y = num/den として除算した結果を出力します。
例
ハードウェア効率に優れた Real Divide HDL Optimized の実装
Real Divide HDL Optimized ブロックの使用方法。
Customize Output Value of Real Divide HDL Optimized Block When Denominator Is Zero
Use the divideByZero port to customize the value of the block output when division by zero occurs.
How to Set CORDIC Input Word Length and Maximum Shift Value to Achieve Desired Precision
Provides a starting point for the input data type and number of iterations or maximum shift value required for the CORDIC algorithm to achieve a desired accuracy.
制限
Real Divide HDL Optimized ブロックではデータ型オーバーライドはサポートされていません。
端子
入力
出力
パラメーター
ヒント
ブロック Divide by Constant HDL Optimized、Real Divide HDL Optimized および Complex Divide HDL Optimized はすべて、除算演算を実行して最適化された HDL コードを生成します。
Real Divide HDL Optimized および Complex Divide HDL Optimized は CORDIC アルゴリズムに基づいています。これらのブロックはさまざまな入力を受け入れますが、レイテンシが大きくなります。
Divide by Constant HDL Optimized は、実数入力と定数除数のみを受け入れます。このブロックを使用すると DSP スライスが消費されますが、除算演算の実行時のサイクル数が減り、クロック レートが高くなります。
アルゴリズム
Real Divide HDL Optimized ブロックは、完全にパイプライン化されるという性質から、連続するサイクルを含む任意のサイクルで入力データを受け入れることができます。入力データをブロックに送信するには、validIn 信号が true でなければなりません。ブロックが計算を終え、出力を送信する準備ができると、1 クロック サイクルの間、validOut を true に変更します。連続するサイクルで送信される入力の場合、連続するサイクルでも validOut が true に設定されます。分子と分母の両方を同じサイクルで一緒に送信しなければなりません。
レイテンシは、表にまとめられているように、入力データ型、パイプライン レジスタごとの反復回数、および双曲線ベクトル CORDIC の最大シフト値によって異なります。表内では以下のようになっています。
入力 num と den の語長は異なっていてもかまいません。
wl = max(num.WordLength + ~issigned(num), den.WordLength + ~issigned(den))[入力の語長に基づいて CORDIC の最大シフト値を自動選択] が
onに設定されている場合、maximumShiftValue = wl - 1になります。[入力の語長に基づいて CORDIC の最大シフト値を自動選択] がoffに設定されている場合、maximumShiftValueは [CORDIC の最大シフト値] パラメーターで指定されます。
| 入力の型 | レイテンシ |
|---|---|
固定小数点またはスケーリングされた double |
|
浮動小数点 | 0 |
参照
[1] Volder, Jack E. “The CORDIC Trigonometric Computing Technique.” IRE Transactions on Electronic Computers. EC-8, no. 3 (Sept. 1959): 330–334.
[2] Andraka, Ray. “A Survey of CORDIC Algorithm for FPGA Based Computers.” In Proceedings of the 1998 ACM/SIGDA Sixth International Symposium on Field Programmable Gate Arrays, 191–200. https://dl.acm.org/doi/10.1145/275107.275139.
[3] Walther, J.S. “A Unified Algorithm for Elementary Functions.” In Proceedings of the May 18-20, 1971 Spring Joint Computer Conference, 379–386. https://dl.acm.org/doi/10.1145/1478786.1478840.
[4] Schelin, Charles W. “Calculator Function Approximation.” The American Mathematical Monthly, no. 5 (May 1983): 317–325. https://doi.org/10.2307/2975781.
