ノイズを含むステップ信号の移動 RMS の計算

この例では次を使用します。

モデルを開く

Moving RMSブロックを使用して、ノイズを含む矩形波信号の移動平方根平均二乗 (RMS) を計算します。スライディング ウィンドウ法 (ホップ サイズ $(window length - overlap length)$ が 5 と 1) と、指数の重み付け法 (忘却係数が 0.9 と 0.99) を使用します。これら 2 つの方法の出力を比較します。これらの方法の詳細については、スライディング ウィンドウ法と指数の重み付け法を参照してください。

モデルを開いて実行する

Pulse Generator (Simulink)ブロックは、幅 512 サンプルの矩形パルス入力信号を生成します。Switch (Simulink)ブロックは、信号の振幅を 1.5 ～ 0.5 の間で変化させます。分散が 0.001 でゼロ平均のホワイト ガウス ノイズを矩形パルスに付加します。入力信号のフレーム長は 512 サンプルです。

4 つの Moving RMS ブロックを使用し、各フレームにわたってこの信号の移動 RMS を計算します。スライディング ウィンドウ法を使用する最初の 2 つの Moving RMS ブロックでは、ウィンドウの長さが 100 に設定され、オーバーラップ長がそれぞれ 95 と 99 に設定されるため、ホップ サイズは 5 と 1 になります。指数の重み付け法を使用する最後の 2 つの Moving RMS ブロックでは、忘却係数はそれぞれ 0.9 と 0.99 に設定されます。出力をTime Scopeで表示して比較します。

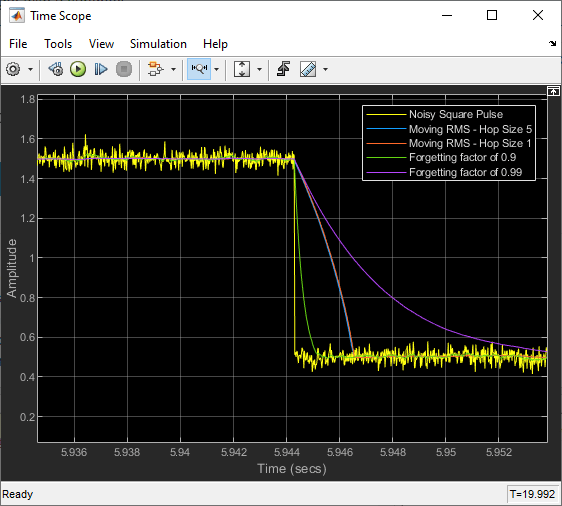
移動 RMS 出力の比較

スライディング ウィンドウの Moving RMS ブロックで、[固定サイズの入力信号に対する任意のフレーム長を許可] パラメーターを選択すると、移動 RMS 出力の次元がホップ サイズに基づいて変化します。入力が 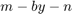$m-by-n$ の場合、出力の上限サイズは $ceil(m/hop size)-by-n$ になります。詳細については、Moving RMSを参照してください。

最後の 2 つのブロックでは指数の重み付け法が使用されます。指数の重み付け法では、この例のように信号が急激に変化する場合は、より小さい忘却係数が使用されます。忘却係数が小さい場合、過去のデータが現在の RMS 出力に与える影響は小さくなります。これにより、出力にノイズが多く含まれている場合でも、過渡特性がより急峻になります。忘却係数 0.9 と 0.99 の移動 RMS 出力を比較することで、この特性を Time Scope で確認できます。

参考

ブロック

トピック