dsp.FFT
離散フーリエ変換
説明
dsp.FFT System object™ は、高速フーリエ変換 (FFT) を使用して入力の離散フーリエ変換 (DFT) を計算します。オブジェクトは、入力が実数/複素数のどちらであるか、また、出力が線形順とビット反転順のどちらであるかに応じて、次の 1 つ以上の高速フーリエ変換 (FFT) アルゴリズムを使用します。
dsp.FFT オブジェクトと fft 関数はどちらも、高速フーリエ変換 (FFT) を使用して離散フーリエ変換 (DFT) を計算します。ただ、オブジェクトは大量のリアルタイム データ ストリームを処理し、システム状態を自動的に処理することができます。関数は、すぐに利用可能かつシステム状態を処理できないデータに対して 1 回限りの計算を実行します。両者の比較については、System object と MATLAB 関数を参照してください。
入力の DFT を計算する方法は次のとおりです。
dsp.FFTオブジェクトを作成し、そのプロパティを設定します。関数と同様に、引数を指定してオブジェクトを呼び出します。
System object の機能の詳細については、System object とはを参照してください。
作成
説明
ft = dsp.FFTFFT オブジェクトを返します。
ft = dsp.FFT(Name=Value)FFTLength を 128 に設定します。
プロパティ
オブジェクト関数
オブジェクト関数を使用するには、System object を最初の入力引数として指定します。たとえば、obj という名前の System object のシステム リソースを解放するには、次の構文を使用します。
release(obj)
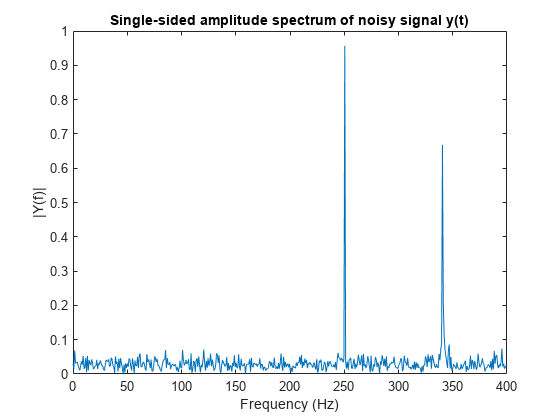
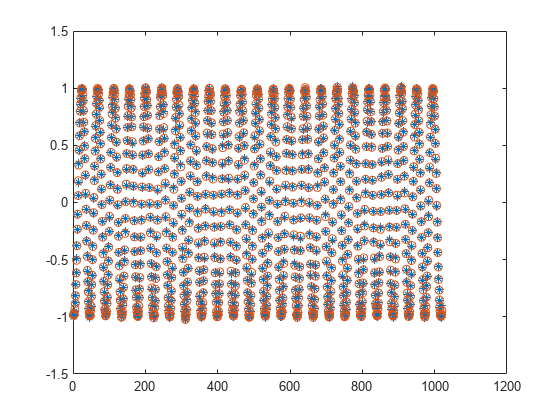
例
アルゴリズム
このオブジェクトは、FFT ブロックのリファレンス ページで説明されているアルゴリズム、入力、および出力を実装しています。オブジェクト プロパティはブロック パラメーターに対応します。
参照
[1] FFTW (https://www.fftw.org)
[2] Frigo, M. and S. G. Johnson, “FFTW: An Adaptive Software Architecture for the FFT,” Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, Vol. 3, 1998, pp. 1381-1384.
拡張機能
バージョン履歴
R2012a で導入