フーリエモデルによる近似

フーリエ級数モデルについて

フーリエ級数は、正弦関数と余弦関数の和として周期関数を記述します。フーリエ級数を使用することにより、任意の周期関数を単純な成分に分割できます。こうした成分は、積分、微分、分析が容易になります。このため、フーリエ級数は周期信号の近似によく使用されます。

フーリエ級数は、いくつかの形式で表されます。Curve Fitting Toolbox™ は、次のような三角関数によるフーリエ級数の形式を使用します。

$y = a_{0} + \sum_{i = 1}^{n} a_{i} \cos (i w x) + b_{i} \sin (i w x)$

ここで、a₀ はデータの定数 (切片) 項をモデル化したものであり、i = 0 の余弦項に関連しています。w は信号の基本周波数、n は項 (高調波) の数です。Curve Fitting Toolbox は、1 ≤ n ≤ 8 についてフーリエ級数回帰をサポートします。

フーリエ級数の詳細については、フーリエ解析とフィルター処理を参照してください。

曲線フィッターアプリにおけるフーリエモデルによる対話的な近似

ライブスクリプトを開く

この例では、曲線フィッターアプリを使用してフーリエモデルをデータに当てはめる方法を示します。

音声信号のサンプルデータを読み込みます。

load gong.mat

変数 y と Fs には、銅鑼の音の音声信号と周波数データがそれぞれ含まれています。y の最初の 1,000 要素を gongClip という名前のベクトルに保存して音声クリップを作成します。

gongClip = y(1:1000);

gongClip 内の各要素に対応する時間を計算するため、要素のインデックスを Fs で除算します。

t = [1:1000]./Fs;

コマンドラインから曲線フィッターアプリを開きます。

curveFitter

または、[アプリ] タブの [数学、統計および最適化] グループで [曲線フィッター] をクリックします。

曲線フィッターアプリで、近似のデータ変数を選択します。[曲線フィッター] タブの [データ] セクションで [データの選択] をクリックします。[近似データの選択] ダイアログボックスで、[X データ] の値として t、[Y データ] の値として gongClip を選択します。

変数を選択すると、アプリによってデータ点がプロットされます。既定で、アプリは多項式をデータに当てはめます。フーリエモデルを当てはめるには、[曲線フィッター] タブの [近似タイプ] セクションで Fourier をクリックします。

アプリは、単項フーリエモデルを当てはめます。

当てはめられた 1 項フーリエモデルは、単純な振動運動をもつ周期関数です。[結果] パネルには、モデルの一般方程式、当てはめられた 95% 信頼区間の係数推定値、基本周波数、適合度の統計量が表示されます。

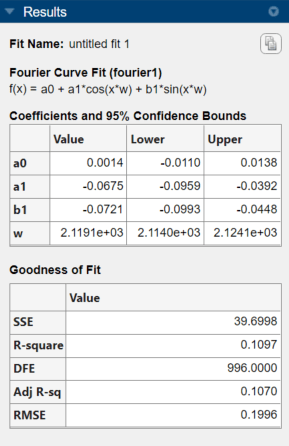
当てはめられた 1 項フーリエモデルの平方根平均二乗誤差 (RMSE) は 0.1996 です。この 1 項フーリエモデルを 4 項フーリエモデルと比較するには、[近似オプション] パネルの [項数] に 4 を選択します。アプリによって、4 項フーリエモデルがデータに当てはめられます。

ここで、当てはめられた 4 項フーリエモデルの方が、1 項フーリエモデルより、振動運動は複雑になります。4 項モデルの RMSE は 0.1685 です。これは、4 項の方が、1 項より正確に音声データを予測していることを示しています。しかし、プロットは、gongClip 内のいくつかのデータ点が 4 項モデルの範囲の外側にあることを示しています。

[エクスポート] セクションの [エクスポート] をクリックし、Export to Workspace を選択して、当てはめられた 4 項フーリエモデルをワークスペースにエクスポートします。ダイアログボックスで、2 つ目と 3 つ目のオプションを解除します。最初のオプションの隣にあるボックスの変数名に近似を保存します。

関数soundを使用すると、gongClip 内の音声データを聞くことができます。

sound(gongClip,Fs)
pause(2)    % Allow gongClip to play before executing next line

gongClip のフーリエモデル近似の音声データを取得するには、fevalを使用して、t 内の時間で gongFourierModel を評価します。近似された音声データを再生します。

gongClipApprox = feval(gongFourierModel,t);
sound(gongClipApprox,Fs)

2 つのクリップは、同じ近似平均トーンをもちます。しかし、近似された音声データのトーン内の変動は、gongClip 内の音声データほど多くありません。

コマンドラインでのフーリエモデルによる近似

ライブスクリプトを開く

この例では、関数fitを使用してフーリエモデルをデータに当てはめる方法を示します。

2 項フーリエモデルによる近似

エルニーニョ南方振動 (ENSO) のデータを読み込みます。

load enso;

変数 pressure には、チリのイースター島とオーストラリアのダーウィンの平均大気圧の差に関するデータが含まれています。変数 month には、各気圧差が生じた月に関するデータが含まれています。

month に対して pressure をプロットします。

plot(month,pressure)

気圧データは 0 から 18 の間で振動しており、これはフーリエ級数で記述できることを示唆しています。

フーリエライブラリモデルを使用して、2 項フーリエモデルを当てはめます。モデルタイプを、fourier の後ろに項数を付けて指定します。後で比較をするために、適合度の統計量を保存します。

[f2,gof2] = fit(month,pressure,"fourier2")

f2 = 
     General model Fourier2:
     f2(x) =  a0 + a1*cos(x*w) + b1*sin(x*w) + 
               a2*cos(2*x*w) + b2*sin(2*x*w)
     Coefficients (with 95% confidence bounds):
       a0 =       10.63  (10.23, 11.03)
       a1 =       2.923  (2.27, 3.576)
       b1 =       1.059  (0.01593, 2.101)
       a2 =     -0.5052  (-1.086, 0.07532)
       b2 =      0.2187  (-0.4202, 0.8576)
       w =      0.5258  (0.5222, 0.5294)

gof2 = struct with fields:
           sse: 1.1230e+03
       rsquare: 0.4279
           dfe: 162
    adjrsquare: 0.4103
          rmse: 2.6329

f2 はcfitオブジェクトです。ここには、近似 w の一般式、95% 信頼限界の係数推定値、基本周波数が含まれます。a2 と b2 の信頼限界はゼロと交差します。このため、それらがゼロではない、つまり当てはめられたモデルが 1 項フーリエモデルではないと結論づける十分な証拠は存在しません。平方根平均二乗誤差 (RMSE) は 2.6329 であり、この値は、f2 の精度と、他の近似の精度を比較するときに役立ちます。

基本周波数から周期を計算するには、式 T = 2*pi/w を使用します。

w = f2.w

w = 0.5258

T = 2*pi/w

T = 11.9497

当てはめられた 2 項フーリエモデルの周期は、おおよそ 12 か月 (1 年) です。

f2 をデータの散布図と一緒にプロットします。

plot(f2,month,pressure)

f2 の形状は 1 項フーリエモデルの形状と似ており、振動のピークがおおよそ 12 か月ごとに発生しています。

7 項フーリエモデルによる近似

7 項フーリエモデルをデータに当てはめます。適合度の統計量を保存します。

[f7,gof7] = fit(month,pressure,"fourier7")

f7 = 
     General model Fourier7:
     f7(x) = 
               a0 + a1*cos(x*w) + b1*sin(x*w) + 
               a2*cos(2*x*w) + b2*sin(2*x*w) + a3*cos(3*x*w) + b3*sin(3*x*w) + 
               a4*cos(4*x*w) + b4*sin(4*x*w) + a5*cos(5*x*w) + b5*sin(5*x*w) + 
               a6*cos(6*x*w) + b6*sin(6*x*w) + a7*cos(7*x*w) + b7*sin(7*x*w)
     Coefficients (with 95% confidence bounds):
       a0 =       10.63  (10.28, 10.97)
       a1 =      0.5669  (0.08285, 1.051)
       b1 =      0.1969  (-0.29, 0.6838)
       a2 =      -1.203  (-1.687, -0.7189)
       b2 =     -0.8085  (-1.307, -0.31)
       a3 =      0.9323  (0.4325, 1.432)
       b3 =      0.7599  (0.2622, 1.258)
       a4 =     -0.6653  (-1.149, -0.1817)
       b4 =     -0.2038  (-0.6995, 0.292)
       a5 =    -0.02913  (-0.5129, 0.4547)
       b5 =     -0.3701  (-0.8566, 0.1164)
       a6 =    -0.04841  (-0.5437, 0.4469)
       b6 =     -0.1367  (-0.6286, 0.3552)
       a7 =       2.812  (2.19, 3.433)
       b7 =       1.333  (0.4017, 2.264)
       w =     0.07527  (0.07478, 0.07576)

gof7 = struct with fields:
           sse: 768.3656
       rsquare: 0.6086
           dfe: 152
    adjrsquare: 0.5700
          rmse: 2.2483

f7 には、信頼限界がゼロと公差する係数がいくつか含まれています。このため、対応する項が、当てはめられたフーリエモデルの精度を高めていると結論づける十分な証拠は存在しません。RMSE は 2.2483 で、f2 の RMSE 誤差より小さい値であり、このことから、7 項フーリエモデルは 2 項フーリエモデルより気圧を正確に予測することが確認されます。

基本周波数から周期を計算するには、式 T = 2*pi/w を使用して周期を計算します。

w = f7.w

w = 0.0753

T = (2*pi)/w

T = 83.4745

当てはめられた 7 項フーリエモデルの周期は、おおよそ 83 か月 (約 7 年) です。当てはめられた係数の振幅は、どの項が気圧差の予測値に最も寄与するかを決定します。

形式 sin(Ax) または cos(Ax) の正弦波の周期は、式 T = 2*pi/|A| で与えられます。a7 と b7 は最大係数です。

T = 2*pi/(w*7)

T = 11.9249

a7 と b7 に対応する項の周期はおおよそ 12 か月であり、これは 1 年サイクルが最も有力であることを示しています。

同じ式を使用して、以下の項の周期を計算します。

項 a1 と b1 は 7 年ごとの周期をもっています。
項 a2 と b2 は 3.5 (7/2) 年ごとの周期をもっています。a2 係数と b2 係数は a1 と b1 より大きな振幅をもっています。このため、3.5 年サイクルの方が、7 年サイクルより、気圧差の予測値に寄与します。
項 a3 と b3 は有力であり、2.3 年 (7/3) サイクルを示しています。

a6、b6、a5、b5 などの小さい項は近似においてあまり重要ではありません。

f7 をデータの散布図と一緒にプロットします。

plot(f7,month,pressure)

7 項フーリエモデルの方が、1 項フーリエモデルより、複雑なパターンで振動しており、気圧差の広い範囲の値をとらえています。サイクルは、おおよそ 84 か月 (7 年) ごとに繰り返しています。通常、エルニーニョによる温度上昇は、2 年から 7 年の不規則な間隔で発生し 9 か月から 2 年続きます。周期の長さの平均は 5 年です。このモデルの結果は、この周期をある程度反映しています。

開始点の設定

関数 fit は、data 入力引数を使用して、係数と基本周波数の計算のために最適化された開始点を計算します。フーリエ級数モデルは開始点の影響を特に受けやすく、最適化された値は対応する方程式のほんのわずかな項についてしか正確ではない場合があります。名前と値の引数 StartPoint を指定することによって、最適化された開始点をオーバーライドできます。

データの散布図内の極端な値は、4 年サイクルが存在する可能性を示唆しています。この可能性を確認するには、基本周波数の開始点を、8 年 (96 か月) の周期に対応する値に設定します。当てはめられたフーリエモデルの 8 年周期では、項 a2 と b2 の周期が 3.5 から 4 に増加します。

w_8 = (2*pi)/96

w_8 = 0.0654

関数coeffnamesを使用して、f7 係数名の cell ベクトルで基本周波数のインデックスを確認します。

coeffnames(f7)

ans = 16x1 cell
    {'a0'}
    {'a1'}
    {'b1'}
    {'a2'}
    {'b2'}
    {'a3'}
    {'b3'}
    {'a4'}
    {'b4'}
    {'a5'}
    {'b5'}
    {'a6'}
    {'b6'}
    {'a7'}
    {'b7'}
    {'w' }

基本周波数は、係数名のベクトルの最後のエントリにあります。f7 の係数から係数値のベクトルを作成し、基本周波数の値を、8 年周期に対応する値で置き換えます。

coeffs = coeffvalues(f7);
coeffs(:,end) = w_8

coeffs = 1×16

   10.6262    0.5669    0.1969   -1.2031   -0.8085    0.9323    0.7599   -0.6653   -0.2038   -0.0291   -0.3701   -0.0484   -0.1367    2.8120    1.3330    0.0654

基本周波数に新しい値をもつ係数を開始点として使用して、7 項フーリエモデルを気圧差データに当てはめます。適合度の統計量を保存します。

[f7_8,gof7_8] = fit(month,pressure,"fourier7",StartPoint=coeffs)

f7_8 = 
     General model Fourier7:
     f7_8(x) = 
               a0 + a1*cos(x*w) + b1*sin(x*w) + 
               a2*cos(2*x*w) + b2*sin(2*x*w) + a3*cos(3*x*w) + b3*sin(3*x*w) + 
               a4*cos(4*x*w) + b4*sin(4*x*w) + a5*cos(5*x*w) + b5*sin(5*x*w) + 
               a6*cos(6*x*w) + b6*sin(6*x*w) + a7*cos(7*x*w) + b7*sin(7*x*w)
     Coefficients (with 95% confidence bounds):
       a0 =       10.58  (10.05, 11.1)
       a1 =      0.3286  (-0.4339, 1.091)
       b1 =    -0.05917  (-0.7884, 0.6701)
       a2 =     -0.8667  (-1.738, 0.004258)
       b2 =       1.094  (0.2819, 1.906)
       a3 =     -0.4524  (-1.232, 0.3272)
       b3 =     -0.3117  (-1.099, 0.4753)
       a4 =       0.181  (-0.7949, 1.157)
       b4 =      0.5806  (-0.1796, 1.341)
       a5 =     0.03263  (-0.7174, 0.7827)
       b5 =     -0.2299  (-0.9767, 0.5169)
       a6 =      0.3726  (-0.39, 1.135)
       b6 =     -0.2745  (-1.165, 0.6161)
       a7 =      0.4309  (-0.491, 1.353)
       b7 =     -0.3547  (-1.316, 0.6062)
       w =     0.06795  (0.06519, 0.0707)

gof7_8 = struct with fields:
           sse: 1.6851e+03
       rsquare: 0.1416
           dfe: 152
    adjrsquare: 0.0568
          rmse: 3.3296

f7_8 の係数は、f7 の係数からわずかにシフトされています。f7_8 の方が RMSE が大きいことは、このデータに対しては f7 の方が適切な近似であることを示しています。両方の近似をプロットしてモデルを視覚的に比較します。

plot(f7_8,month,pressure)
hold on
plot(f7, 'b')
hold off
legend("Data","f7_8","f7")

プロットは、f7 の方が、f7_8 より、気圧差データ内の変動を正確にとらえていることを示しています。

フーリエ近似反復の表示

名前と値の引数を使って追加のオプションを指定する代わりに、fitoptions オブジェクトを関数 fit に渡します。フーリエモデル近似に使用できるオプションを表示するには、関数fitoptionsへの入力引数としてモデル名を渡します。

fitoptions("fourier7")

ans = 
  nlsqoptions with properties:

       StartPoint: []
            Lower: []
            Upper: []
        Algorithm: 'Trust-Region'
    DiffMinChange: 1.0000e-08
    DiffMaxChange: 0.1000
          Display: 'Notify'
      MaxFunEvals: 600
          MaxIter: 400
           TolFun: 1.0000e-06
             TolX: 1.0000e-06
           Robust: 'Off'
        Normalize: 'off'
          Exclude: []
          Weights: []
           Method: 'NonlinearLeastSquares'

fitoptions オブジェクトを作成し、各反復の後に出力を表示するように指定します。

optionsf7 = fitoptions("fourier7",Display="iter")

optionsf7 = 
  nlsqoptions with properties:

       StartPoint: []
            Lower: []
            Upper: []
        Algorithm: 'Trust-Region'
    DiffMinChange: 1.0000e-08
    DiffMaxChange: 0.1000
          Display: 'Iter'
      MaxFunEvals: 600
          MaxIter: 400
           TolFun: 1.0000e-06
             TolX: 1.0000e-06
           Robust: 'Off'
        Normalize: 'off'
          Exclude: []
          Weights: []
           Method: 'NonlinearLeastSquares'

optionsf7 は、7 項フーリエモデル近似のオプションを含む fitoptions オブジェクトです。

f7 の作成に関係する反復ステップを表示するには、optionsf7 内のオプションを使用して別の 7 項フーリエモデルを当てはめます。

f7_iter = fit(month,pressure,"fourier7",optionsf7)

                                         Norm of      First-order 
 Iteration  Func-count     f(x)          step          optimality   CG-iterations
     0          2          768.41                      1.93e+03
     1          4         768.366     2.2176e-05           69.1            0
     2          6         768.366    7.94962e-07           2.48            0
Success, but fitting stopped because change in residuals less than tolerance (TolFun).

f7_iter = 
     General model Fourier7:
     f7_iter(x) = 
               a0 + a1*cos(x*w) + b1*sin(x*w) + 
               a2*cos(2*x*w) + b2*sin(2*x*w) + a3*cos(3*x*w) + b3*sin(3*x*w) + 
               a4*cos(4*x*w) + b4*sin(4*x*w) + a5*cos(5*x*w) + b5*sin(5*x*w) + 
               a6*cos(6*x*w) + b6*sin(6*x*w) + a7*cos(7*x*w) + b7*sin(7*x*w)
     Coefficients (with 95% confidence bounds):
       a0 =       10.63  (10.28, 10.97)
       a1 =      0.5669  (0.08285, 1.051)
       b1 =      0.1969  (-0.29, 0.6838)
       a2 =      -1.203  (-1.687, -0.7189)
       b2 =     -0.8085  (-1.307, -0.31)
       a3 =      0.9323  (0.4325, 1.432)
       b3 =      0.7599  (0.2622, 1.258)
       a4 =     -0.6653  (-1.149, -0.1817)
       b4 =     -0.2038  (-0.6995, 0.292)
       a5 =    -0.02913  (-0.5129, 0.4547)
       b5 =     -0.3701  (-0.8566, 0.1164)
       a6 =    -0.04841  (-0.5437, 0.4469)
       b6 =     -0.1367  (-0.6286, 0.3552)
       a7 =       2.812  (2.19, 3.433)
       b7 =       1.333  (0.4017, 2.264)
       w =     0.07527  (0.07478, 0.07576)

フーリエモデル近似についてさらに調べるには、NonlinearLeastSquares 近似アルゴリズムにおいて使用可能なさまざまなオプションを指定して試すことができます。詳細については、fitoptionsを参照してください。