ENSO データのカスタム非線形解析

この例では、いくつかのカスタム非線形方程式を使用して ENSO データに当てはめます。ENSO データは、イースター島とオーストラリアのダーウィン間における大気圧の差の月平均で構成されています。この差により南半球の貿易風が発生します。

ENSO データは明らかに周期的であり、フーリエ級数で記述できることを示唆しています。

$y (x) = a_{0} + \sum_{i = 1}^{\infty} a_{i} \cos (2 π \frac{x}{c_{i}}) + b_{i} \sin (2 π \frac{x}{c_{i}})$

ここで、a_i および b_i は振幅、c_i はデータの周期 (サイクル) です。サイクルをいくつ存在させるかを決定します。

最初の試みとして、単一サイクルを仮定し、余弦項と正弦項を 1 つずつ使用してデータに当てはめます。

$y_{1} (x) = a_{0} + a_{1} \cos (2 π \frac{x}{c_{1}}) + b_{1} \sin (2 π \frac{x}{c_{1}})$

この近似でデータがうまく記述されない場合は、適切な近似が得られるまで一意の周期係数を含む余弦項と正弦項を追加します。

未知の係数 c₁ が三角関数の引数の一部として含まれているため、この方程式は非線形です。

データの読み込みとライブラリおよびカスタムのフーリエモデルによる近似

データを読み込み、曲線フィッターアプリを開きます。
```
load enso
curveFitter
```
アプリにはフーリエ級数が非線形ライブラリ方程式として含まれています。ただし、ライブラリ方程式は、項が基本周波数 w の定数倍として定義されているため、この例のニーズを満たしません。詳細については、フーリエモデルによる近似を参照してください。組み込みライブラリフーリエ近似を作成し、カスタム式と比較します。
1. アプリ内の [曲線フィッター] タブで、[データ] セクションの [データの選択] をクリックします。[近似データの選択] ダイアログボックスで、[X データ] の値として month、[Y データ] の値として pressure を選択します。
2. [曲線フィッター] タブの [近似タイプ] セクションで、矢印をクリックしてギャラリーを開きます。近似ギャラリーで、[回帰モデル] グループの [フーリエ] をクリックします。
3. [近似テーブル] ペインで、[近似名] の値をダブルクリックして Fourier と入力します。
4. [近似オプション] ペインで、項数を [8] に変更します。
  ライブラリモデル近似を観察します。以下の手順で、比較するカスタム式を作成します。
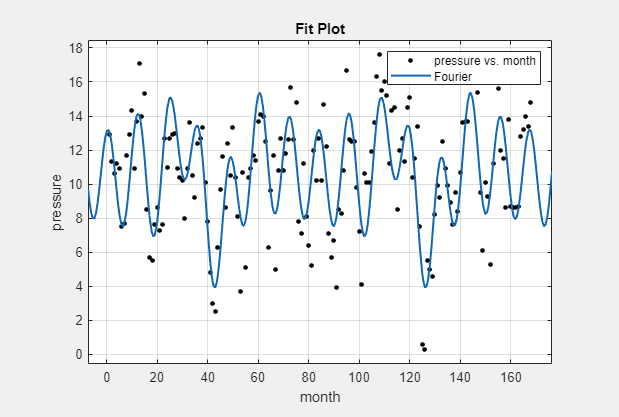
近似を複製します。[近似テーブル] ペインで近似を右クリックし、["Fourier" を複製] を選択します。
新しい近似に Enso1Period という名前を付けます。
[曲線フィッター] タブの [近似タイプ] セクションで、近似タイプのギャラリーを開き、[カスタム] グループの [カスタム式] をクリックします。
[近似オプション] ペインで、方程式のエディットボックスに例として入力されているテキストを、次の内容に置き換えます。
```
a0 + a1*cos(2*pi*x/c1) + b1*sin(2*pi*x/c1)
```
enso データに近似が適用されます。

このグラフィカルな結果と数値的な結果は、近似でデータが適切に記述されていないことを示しています。特に、c1 の近似値が極端に小さくなっています。開始点はランダムに選択されるため、最初の近似結果はこれらの結果と異なる場合があります。

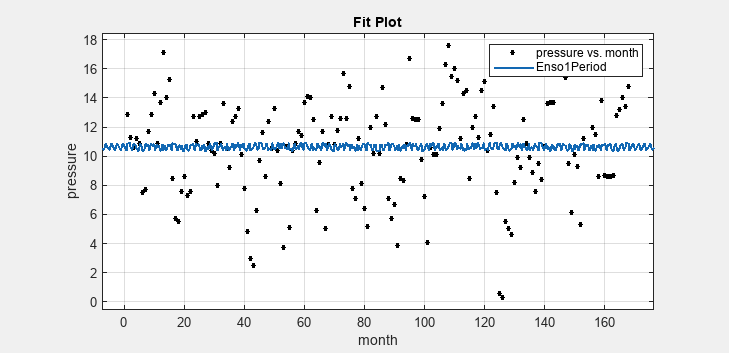
Custom equation fit plot for the ENSO data

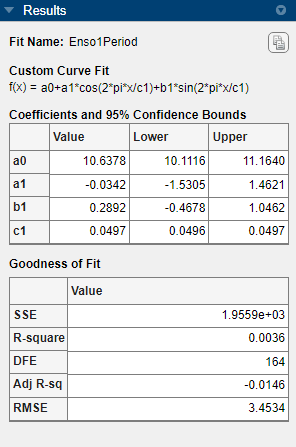
Results pane for the custom equation fit to the ENSO data

既定の設定では、係数に範囲の制限がなく、係数の開始値は 0 から 1 までのランダムな値です。このデータには周期が約 12 か月の周期的な成分が含まれています。しかし、c1 に制約がなく開始点がランダムであるこの近似では、このサイクルを見つけることができませんでした。

近似オプションによる係数の制約

近似手順を支援するため、c1 の値を 10 から 14 までに制約します。[近似オプション] ペインで、[詳細オプション] をクリックしてセクションを展開し、係数の制約を表示します。既定の設定では係数に範囲の制約がない (範囲が -Inf から Inf までである) ことを観察します。
[係数の制約] テーブルで、c1 の [下限] と [上限] を次に示すように変更し、サイクルを 10 か月から 14 か月までに制約します。
曲線フィッターアプリにより、近似が更新されます。
新しい近似と残差のプロットを観察します。必要な場合は、[曲線フィッター] タブの [可視化] セクションにある [残差プロット] をクリックします。
この近似は一部のデータ点については妥当であるように見えますが、明らかにデータセット全体を十分に記述できていません。予想どおり、[結果] ペインの数値結果 (c1=11.94) はサイクルがおよそ 12 か月であることを示しています。ただし、残差には体系的な周期分布が見られ、少なくとももう 1 つのサイクルが存在することを示しています。近似方程式に含める必要がある追加のサイクルが存在します。

項と制約を追加した 2 番目のカスタム近似の作成

近似を調整するために、次のように y₁(x) に正弦項と余弦項を追加する必要があります。

$y_{2} (x) = y_{1} (x) + a_{2} \cos (2 π \frac{x}{c_{2}}) + b_{2} \sin (2 π \frac{x}{c_{2}})$

さらに、c₂ の上限と下限を c₁ に使用される範囲のおよそ 2 倍に制約します。

[近似テーブル] ペインで近似を右クリックし、["Enso1Period" を複製] を選択して近似を複製します。
新しい近似に Enso2Period という名前を付けます。
[近似オプション] ペインで、前の方程式の末尾に項を 2 つ追加し、方程式ボックスに次のような項が表示されるようにします。
```
a0 + a1*cos(2*pi*x/c1) + b1*sin(2*pi*x/c1) + 
a2*cos(2*pi*x/c2) + b2*sin(2*pi*x/c2)
```
[詳細オプション] をクリックしてセクションを展開します。[係数の制約] テーブルで、c1 の [下限] と [上限] により、引き続きサイクルが 10 か月から 14 か月までに制約されていることを観察します。さらに係数の制約を追加します。
1. c2 の [下限] と [上限] を c1 に使用される範囲のおよそ 2 倍 (20<c2<30) になるように変更します。
2. a0 の [開始点] を 5 に変更します。
各設定を変更すると、曲線フィッターアプリによって近似が更新されます。近似プロットと残差プロットを観察できます。

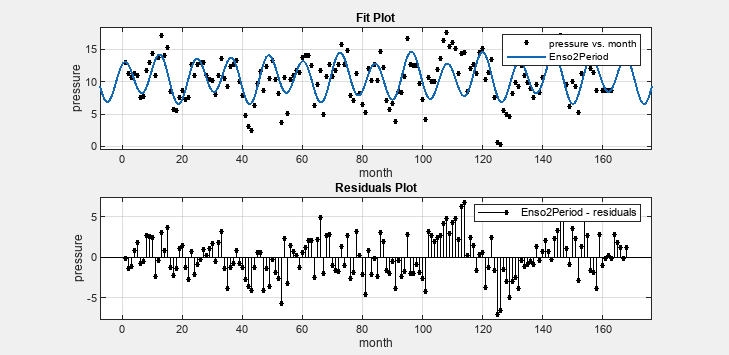
Fit and residuals plots for the Enso2Period fit

近似は大部分のデータ点について妥当であるように見えます。ただし、残差は別のサイクルを近似方程式に含める必要があることを示しています。

項と制約を追加した 3 番目のカスタム近似の作成

3 番目の試みとして、y₂(x) に正弦項と余弦項を追加します。

$y_{3} (x) = y_{2} (x) + a_{3} \cos (2 π \frac{x}{c_{3}}) + b_{3} \sin (2 π \frac{x}{c_{3}})$

さらに、c₃ の下限を c₁ の値のおよそ 3 倍に制約します。

[近似テーブル] ペインで近似を右クリックし、["Enso2Period" を複製] を選択して近似を複製します。
新しい近似に Enso3Period という名前を付けます。
[近似オプション] ペインで、前の方程式の末尾に項を 2 つ追加し、方程式ボックスに次のような項が表示されるようにします。
```
a0 + a1*cos(2*pi*x/c1) + b1*sin(2*pi*x/c1) + 
a2*cos(2*pi*x/c2) + b2*sin(2*pi*x/c2) +
a3*cos(2*pi*x/c3) + b3*sin(2*pi*x/c3)
```
[詳細オプション] をクリックしてセクションを展開します。前の近似オプションが引き続き存在することを観察します。
[係数の制約] テーブルで、c3 の [下限] を、c1 の値のおよそ 3 倍である 36 に変更します。
各設定を変更すると、曲線フィッターアプリによって近似が更新されます。近似プロットと残差プロットを観察できます。

Fit and residuals plots for the Enso3Period fit

近似は前の 2 つの近似よりも改善されており、ENSO データセットのサイクルの大部分を説明しているように見えます。残差は大部分のデータについてランダムであるように見えます。ただし、追加のサイクルが存在する可能性がある、または振幅の近似を改善できることを示すパターンが依然として確認できます。

結論として、データのフーリエ解析により 3 つの主要なサイクルがあることが明らかになりました。1 年サイクルが最も有力ですが、約 44 か月および 22 か月のサイクルも存在します。これらのサイクルは、エルニーニョ南方振動 (ENSO) に対応しています。