ゲイン スケジュールのパラメーター化
通常、Simulink® 内のゲイン スケジュール制御システムは、ルックアップ テーブルまたは MATLAB Function ブロックを使用してゲイン値をスケジューリング変数の関数として指定します。調整のため、これらのブロックをパラメトリックなゲイン曲面で置き換えます。"パラメトリックなゲイン曲面"は、係数が調整可能な基底関数の拡張です。たとえば、次のように時変ゲイン k(t) を t で 3 次多項式としてモデル化できます。
k(t) = k0 + k1t + k2t2 + k3t3.
ここで、k0,...,k3 は調整可能な係数です。このようにスケジュール ゲインをパラメーター化する場合、systune で、代表的な一連の操作条件において制御目標が満たされるようゲイン曲面係数を調整できます。ゲインがスケジューリング変数によって滑らかに変化するアプリケーションの場合、この方法ではゲインの明示的な式が与えられ、ソフトウェアはこれを MATLAB Function ブロックに直接書き込むことができます。ルックアップ テーブルを使用する場合、この方法では多数の個別のルックアップ テーブル エントリではなく、いくつかの係数を調整できるため、パラメーター数が大幅に削減され、操作点間の滑らかな遷移が確保されます。
基底関数のパラメーター化
ゲイン スケジュール コントローラーでは、スケジュール ゲインは、スケジューリング変数 σ の関数です。たとえば、ゲイン スケジュール PI コントローラーの形式は次のようになります。
このコントローラーを調整するには、σ 値の動作範囲で最適なシステム パフォーマンスを実現する関数形式 Kp(σ) および Ki(σ) を決定する必要があります。ただし、任意の関数の調整は困難です。したがって、点の有限集合のみの値を考慮するか、関数そのものの一般性を制限します。
1 つ目のアプローチでは、設計点の集合 σ を選択し、各設計点のゲイン Kp と Ki を個別に調整します。結果のゲイン値の集合は、スケジューリング変数 σ で駆動されるルックアップ テーブルに保存されます。このアプローチの欠点は、調整によって隣接する設計点に対して大幅に異なる値が出力され、ある操作点から別の操作点への移行時に望ましくない跳ね上がりが生じることです。
また、σ の滑らかな関数としてゲインをモデル化できますが、特定の基底関数の拡張を使用したこのような関数の一般性は制限されます。たとえば、σ がスカラー変数であるとします。Kp(σ) は次のように σ の二次関数としてモデル化できます。
調整後、このパラメトリック ゲインには次のようなプロファイルが含まれる可能性があります (曲線の特定の形状は、σ の調整後の係数値と範囲に応じて異なります)。

または、σ が 2 つのスケジューリング変数 α と V で構成されているとします。この場合は、Kp(σ) を次のように α と V の双一次関数としてモデル化できます。
調整後、パラメトリック ゲインには次のようなプロファイルが含まれる可能性があります。ここでも、曲線の特定の形状は σ 値の調整後の係数と範囲に応じて異なります。
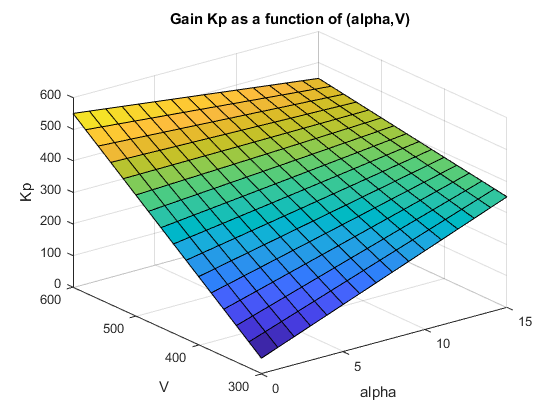
systune でゲイン スケジュールを調整する場合は、σ の基底関数のゲインの特定の拡張である "パラメトリックなゲイン曲面" を使用します。
基底関数 F1,...,FM はユーザーが選択し、固定されます。これらの関数は n(σ) に対して機能します。ここで n は、スケジューリング変数を区間 [–1,1] (または指定した区間) にスケール変換して正規化する関数です。拡張の係数 K0,...,KM は、ゲイン曲面の調整可能なパラメーターです。K0,...,KM は、ゲイン K(σ) の I/O サイズに応じてスカラー値または行列値になります。基底関数の選択は問題により異なりますが、通常はまず低次の多項式の拡張を試してみます。
調整可能なゲイン曲面
tunableSurface コマンドを使用して、設計点 (σ 値) のグリッドでサンプリングされたゲイン曲面の調整可能なモデルを作成します。たとえば、2 つのスケジューリング変数 α および V において双線形な依存関係をもつゲインについて考えてみます。
α は 0 ~ 15 ° の入射角、V は 300 ~ 700 m/s の速度であるとします。これらの範囲にわたる設計点のグリッドを作成します。これらの設計点は、可変または非線形のプラントをサンプリングするときのパラメーター値と一致しなければなりません。(ゲイン スケジュール コントローラー調整のプラント モデルを参照。)
[alpha,V] = ndgrid(0:5:15,300:100:700); domain = struct('alpha',alpha,'V',V);
この曲面のパラメーター化 α、V および αV の基底関数を指定します。tunableSurface コマンドでは、基底関数を 2 つの入力変数の関数のベクトルとして用意するものと想定しています。無名関数を使用して基底関数を表すことができます。
shapefcn = @(alpha,V)[alpha,V,alpha*V];
あるいは、polyBasis、fourierBasis または ndBasis を使用して、必要な数のスケジューリング変数の基底関数を生成します。
設計点と基底関数を使用して調整可能な曲面を作成します。
Kp = tunableSurface('Kp',1,domain,shapefcn);Kp はゲイン曲面の調整可能なモデルです。tunableSurface は曲面を次のようにパラメーター化します。
ここで、
曲面は、α および V ではなく、正規化された変数 によって表されます。この正規化は tunableSurface により既定で実行され、systune が行う最適化の条件を改善します。必要に応じて、既定のスケーリングと正規化を変更できます。(tunableSurface を参照)。
tunableSurface の 2 番目の入力引数では、定数係数の初期値 K0 を指定します。既定では、K0 はすべてのスケジューリング変数がその範囲の中心にあるときのゲインです。tunableSurface は、ゲイン曲面の I/O 次元を K0 から取得します。したがって、この入力の配列を指定して、配列値の調整可能なゲインを作成できます。
Karr = tunableSurface('Karr',ones(2),domain,shapefcn);Karr は 2 行 2 列の行列で、その各エントリは、独立した係数をもつスケジューリング変数の双一次関数となります。
2 つの独立したスケジューリング変数をもつ調整可能なゲイン
この例では、2 つのスケジューリング変数に双線形従属する、スカラー ゲイン K をモデル化する方法を説明します。そのためには、2 つの変数の独立した依存関係を表す設計点のグリッドを作成します。
最初の変数 α は 0 ~ 15 度の範囲の入射角で、2 番目の変数 V は 300 ~ 600 m/s の範囲の速度であると仮定します。既定では、正規化された変数が以下のようになります。
ゲイン曲面は次のようにモデル化されます。
ここで は調整可能なパラメーターです。
α および V に線形に等間隔な設計点のグリッド (α、V) を作成します。これらの設計点は、ゲイン曲面の係数の調整に使用されるスケジューリング変数の値です。プラントをサンプリングしたパラメーターの値と対応していなければなりません。
[alpha,V] = ndgrid(0:3:15,300:50:600);
これらの配列 alpha および V は、2 つのスケジューリング変数の独立した変化を、それぞれが全範囲にわたって表します。これらを構造体に含めて、調整可能な曲面の設計点を定義します。
domain = struct('alpha',alpha,'V',V);
双一次展開を記述する基底関数を作成します。
shapefcn = @(x,y) [x,y,x*y]; % or use polyBasis('canonical',1,2)shapefcn から返された配列内にある基底関数は、次のとおりです。
調整可能なゲイン曲面を作成します。
K = tunableSurface('K',1,domain,shapefcn);調整可能な曲面は、パラメーター化として、Simulink モデルのルックアップ テーブル ブロックまたは MATLAB Function ブロックで使用できます。あるいは、モデル相互接続コマンドを使用して、MATLAB でモデル化された制御システムに調整可能な要素として組み込みます。係数の調整の後は、viewSurf コマンドを使用して結果のゲイン曲面を調べることができます。この例では、調整する代わりに係数をゼロ以外の値に手動で設定し、結果のゲインを表示しています。
Ktuned = setData(K,[100,28,40,10]); viewSurf(Ktuned)
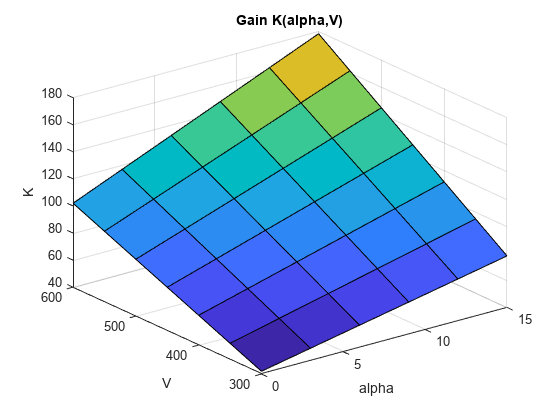
viewSurf を実行すると、domain で指定されゲイン曲面の SamplingGrid プロパティに格納されている値の範囲に対して、ゲイン曲面がスケジューリング変数の関数として表示されます。
Simulink の調整可能な曲面
Simulink モデルでは、Simulink でのゲイン スケジュール制御システムのモデル化で説明されているように、ルックアップ テーブル ブロック、MATLAB Function ブロック、または Matrix Interpolation ブロックを使用してゲイン スケジュールをモデル化します。これらのゲイン曲面を調整するには、tunableSurface を使用して各ブロックにゲイン曲面を作成します。モデルの slTuner インターフェイスで、各ゲイン スケジュールを調整対象のブロックとして指定し、そのパラメーター化を対応するゲイン曲面に設定します。たとえば、rct_CSTR モデルにはゲイン スケジュール PI コントローラーである Concentration controller サブシステムが含まれ、その中で、ゲインの Kp および Ki がスケジューリング変数 Cr により変化します。

ルックアップ テーブルの Kp および Ki を調整するには、それぞれに調整可能な曲面を作成します。CrEQ が設計点のベクトルであり、ゲインは Cr を使って二次的に変動することが予想されると仮定します。
TuningGrid = struct('Cr',CrEQ); ShapeFcn = @(Cr) [Cr , Cr^2]; Kp = tunableSurface('Kp',0,TuningGrid,ShapeFcn); Ki = tunableSurface('Ki',-2,TuningGrid,ShapeFcn);
CrEQ の各設計点にプラント サブシステム CSTR の線形化の配列 Gd があるとします。(ゲイン スケジュール コントローラー調整のプラント モデルを参照)。プラント サブシステムの代わりにこの配列を使用し、調整用に 2 つのルックアップ テーブル ブロックを指定する slTuner インターフェイスを作成します。
BlockSubs = struct('Name','rct_CSTR/CSTR','Value',Gd); ST0 = slTuner('rct_CSTR',{'Kp','Ki'},BlockSubs);
最後に、調整可能な曲面を使ってルックアップ テーブルをパラメーター化します。
ST0.setBlockParam('Kp',Kp); ST0.setBlockParam('Ki',Ki);
STO を調整すると、systune は調整可能な曲面の係数 Kp と Ki を調整し、それぞれの調整可能な曲面が Cr とゲイン間の調整後の関係を表すようになります。検証のために調整後の値をブロックに書き戻すと、setBlockParam は、対応するブロックに指定したブレークポイントで調整可能な曲面を評価することにより、調整後のルックアップ テーブル データを自動的に生成します。
この例の詳細については、化学反応器のゲイン スケジュール制御を参照してください。
MATLAB の調整可能な曲面
MATLAB® でモデル化された制御システムでは、調整可能な曲面を使用して、ゲイン スケジュール PID コントローラー、フィルター、状態空間コントローラーなど、より複雑なゲイン スケジュール制御要素を作成します。たとえば、tunableSurface を使用して 2 つのゲイン曲面 Kp および Ki を作成するとします。次のコマンドで、調整可能なゲイン スケジュール PI コントローラーを構築します。
C0 = pid(Kp,Ki);
同様に、4 つの行列値ゲイン曲面 A、B、C、D を作成するとします。次のコマンドで、調整可能なゲイン スケジュール状態空間コントローラーを構築します。
C1 = ss(A,B,C,D);
次に、ゲイン スケジュール コントローラーを制御システム全体の一般化モデルに組み込みます。たとえば、G は、Kp および Ki で指定されている設計点でサンプリングされたプラントのモデルの配列であるとします。次に、以下のコマンドで、ゲイン スケジュール単一ループ PID 制御システムの調整可能なモデルを作成します。
T0 = feedback(G*C0,1);
調整可能な曲面を他の LTI モデルと相互接続すると、結果のモデルは調整可能な一般化 genss モデルの配列になります。配列の次元は調整可能な曲面の設計点によって決まります。したがって、配列の各エントリは、対応するスケジューリング変数値におけるシステムを表します。配列の SamplingGrid プロパティには、これらの設計点が保存されます。
T0 = feedback(G*Kp,1)
T0 =
4x5 array of generalized continuous-time state-space models.
Each model has 1 outputs, 1 inputs, 3 states, and the following blocks:
Kp: Parametric 1x4 matrix, 1 occurrences.
Type "ss(T0)" to see the current value, "get(T0)" to see all properties, and
"T0.Blocks" to interact with the blocks.結果の一般化モデルには、モデルの作成に使用されたゲイン曲面に対応する調整可能なブロックが含まれます。この例では、システムに 1 つのゲイン曲面 Kp が含まれます。この曲面には K0、K1、K2 および K3 に対応する 4 つの調整可能な係数が含まれます。したがって、調整可能なブロックは、4 つのエントリをもつベクトル値パラメーター realp になります。
systune で制御システムを調整すると、調整可能な曲面で指定された各設計点の係数が調整されます。
MATLAB でのワークフロー全体を表す例は、化学反応器のゲイン スケジュール制御にある「MATLAB でのコントローラーの調整」の節を参照してください。