調整可能なモデルの作成

この例では、systune または looptune で使用する制御システムの調整可能なモデルを作成する方法を示します。

背景

systune または looptune では、制御システムのゲインやパラメーターを調整できます。これらのコマンドを使用するには、制御システムの調整可能な要素を識別してパラメーター化する調整可能なモデルを作成する必要があります。これは、固定要素の数値 LTI モデルと調整可能な要素のパラメトリックモデルを組み合わせることで行います。

事前定義された調整可能な要素の使用

次のいずれかの "パラメトリック" ブロックを使用して、よく使用される調整可能な要素をモデル化できます。

tunableGain: 調整可能なゲイン
tunablePID: 調整可能な PID コントローラー
tunablePID2: 調整可能な 2 自由度の PID コントローラー
tunableTF: 調整可能な伝達関数
tunableSS: 調整可能な状態空間モデル

たとえば、図 1 のフィードフォワード/フィードバック構成の調整可能なモデルを作成します。ここで、 $C$ は調整可能な PID コントローラー、 $F$ は調整可能な 1 次伝達関数です。

図 1: フィードフォワードパスとフィードバックパスを使用した制御システム

まず、 $C$ と $F$ に適切なパラメトリックブロックを使用して、ブロック線図の各ブロックをモデル化します。

G = tf(1,[1 1]); 
C = tunablePID('C','pid');  % tunable PID block
F = tunableTF('F',0,1);     % tunable first-order transfer function

次に、connect を使用してブロック線図全体のモデルを作成します。ブロックの接続方法を指定するために、各ブロックの入力と出力にラベルを付け、sumblk を使用して加算結合をモデル化します。

G.u = 'u';  G.y = 'y';
C.u = 'e';  C.y = 'uC';
F.u = 'r';  F.y = 'uF';

% Summing junctions
S1 = sumblk('e = r-y');
S2 = sumblk('u = uF + uC');

T = connect(G,C,F,S1,S2,'r','y')

Generalized continuous-time state-space model with 1 outputs, 1 inputs, 3 states, and the following blocks:
  C: Tunable PID controller, 1 occurrences.
  F: Tunable SISO transfer function, 0 zeros, 1 poles, 1 occurrences.
Model Properties

Type "ss(T)" to see the current value and "T.Blocks" to interact with the blocks.

これで、r から y への閉ループ伝達関数の一般化状態空間モデル T が作成されます。このモデルは調整可能なブロック C および F に依存します。systune を使用して、PID ゲインおよびフィードフォワード係数 a,b を性能要件に従って自動的に調整できます。調整可能なブロックの現在の値を表示するには、showTunable を使用します。

showTunable(T)

C =
 
        1 
  Ki * ---
        s 

  with Ki = 0.001
 
Name: C
Continuous-time I-only controller.
-----------------------------------
F =
 
    10
  ------
  s + 10
 
Name: F
Continuous-time transfer function.

調整可能なパラメーターの操作

オブジェクト C および F を操作することで、調整可能な要素 $C$ および $F$ のパラメーター化を調整できます。プロパティのリストを表示するには、get を使用します。

get(C)

             Kp: [1×1 param.Continuous]
             Ki: [1×1 param.Continuous]
             Kd: [1×1 param.Continuous]
             Tf: [1×1 param.Continuous]
       IFormula: ''
       DFormula: ''
      InputName: {'e'}
      InputUnit: {''}
     InputGroup: [1×1 struct]
     OutputName: {'uC'}
     OutputUnit: {''}
    OutputGroup: [1×1 struct]
          Notes: [0×1 string]
       UserData: []
           Name: 'C'
             Ts: 0
       TimeUnit: 'seconds'

PID コントローラーには、Kp,Ki,Kd,Tf の 4 つの調整可能なパラメーターがあります。それらの各パラメーターの記述は調整可能なブロック C に格納されています。パラメーターの属性には、現在の値、最小値と最大値、パラメーターが自由か固定かなどの情報が含まれます。

C.Kp

 
ans =
 
       Name: 'Kp'
      Value: 0
    Minimum: -Inf
    Maximum: Inf
       Free: 1
      Scale: 1
       Info: [1×1 struct]

 
1x1 param.Continuous

既定の設定をオーバーライドするには、対応する属性を設定します。たとえば、時定数 Tf の値を 0.1 に固定するには、次のように指定します。

C.Tf.Value = 0.1;
C.Tf.Free = false;

カスタムの調整可能な要素の作成

前述の事前定義されたブロックでカバーされていない調整可能な要素については、基本の実数パラメーター (realp) で独自のパラメーター化を作成できます。次のローパスフィルターについて考えてみます。

$F (s) = \frac{a}{s + a}$

ここで、係数 $a$ は調整可能です。この調整可能な要素をモデル化するには、実数パラメーター $a$ を作成し、分子と分母が $a$ の関数である伝達関数として $F$ を定義します。これにより、調整可能なスカラー a でパラメーター化されたローパスフィルターの一般化状態空間モデル F が作成されます。

a = realp('a',1);   % real tunable parameter, initial value 1
F = tf(a,[1 a])

Generalized continuous-time state-space model with 1 outputs, 1 inputs, 1 states, and the following blocks:
  a: Scalar parameter, 2 occurrences.
Model Properties

Type "ss(F)" to see the current value and "F.Blocks" to interact with the blocks.

同様に、実数パラメーターを使用してノッチフィルターもモデル化できます。

$N (s) = \frac{s^{2} + 2 ζ_{1} ω_{n} s + ω_{n}^{2}}{s^{2} + 2 ζ_{2} ω_{n} s + ω_{n}^{2}}$

$ω_{n}, ζ_{1}, ζ_{2}$ は調整可能な係数です。

wn = realp('wn',100);
zeta1 = realp('zeta1',1);   zeta1.Maximum = 1;    % zeta1 <= 1
zeta2 = realp('zeta2',1);   zeta2.Maximum = 1;    % zeta2 <= 1
N = tf([1 2*zeta1*wn wn^2],[1 2*zeta2*wn wn^2]);  % tunable notch filter

また、行列値のパラメーターを使用して調整可能な要素を作成することもできます。たとえば、次の方程式で表されるオブザーバーベースのコントローラー $C (s)$ をモデル化します。

$\frac{d x}{d t} = A x + B u + L (y - C x), u = - K x$

$K$ と $L$ は調整可能なゲイン行列です。

% Plant with 6 states, 2 controls, 3 measurements
[A,B,C] = ssdata(rss(6,3,2));

K = realp('K',zeros(2,6));
L = realp('L',zeros(6,3));

C = ss(A-B*K-L*C,L,-K,0)

Generalized continuous-time state-space model with 2 outputs, 3 inputs, 6 states, and the following blocks:
  K: Tunable 2x6 matrix, 2 occurrences.
  L: Tunable 6x3 matrix, 2 occurrences.
Model Properties

Type "ss(C)" to see the current value and "C.Blocks" to interact with the blocks.

開ループ要件の有効化

systune コマンドは、この例で最初に作成した調整可能なモデル T のような、制御システム全体の閉ループモデルを受け取ります。このようなモデルでは、このままでは開ループ解析や開ループ仕様 (ループ整形や安定余裕など) はサポートされません。開ループ応答にアクセスできるようにするには、図 2 に示すように AnalysisPoint ブロックを挿入します。

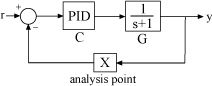
図 2: Analysis Point ブロック

AnalysisPoint ブロックを使用することで、対象とする内部信号に加え、フィードバックループを開く位置と開ループ応答を測定する位置をマークできます。このブロックは単位ゲインと評価され、モデルの応答には影響しません。たとえば、図 2 のフィードバックループの閉ループモデル T を作成します。ここで、 $C$ は調整可能な PID です。

G = tf(1,[1 1]);
C = tunablePID('C','pid');
AP = AnalysisPoint('X');
T = feedback(G*C,AP);

これで、getLoopTransfer を使用して、位置 "X" で測定された (負のフィードバックの) ループ伝達関数を計算することができます。このループ伝達関数は、図 2 のフィードバックループでは $L = G C$ です。

L = getLoopTransfer(T,'X',-1);  % loop transfer at "X"
clf, bode(L,'b',G*C,'r--')

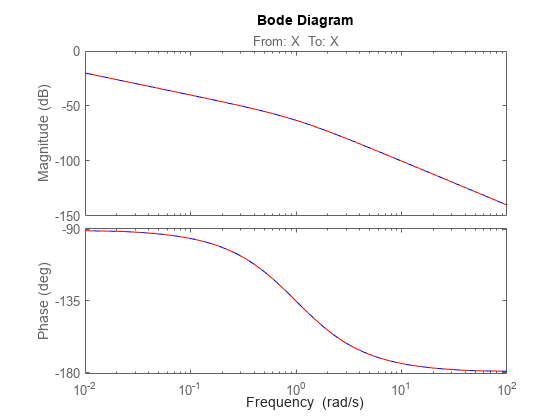
MATLAB figure

systune にターゲットのループ整形や安定余裕を指定するときは、位置 "X" を参照することもできます。この場合、その位置で測定されたループ伝達に要件が適用されます。

% Target loop shape for loop transfer at "X"
Req1 = TuningGoal.LoopShape('X',tf(5,[1 0]));

% Target stability margins for loop transfer at "X"
Req2 = TuningGoal.Margins('X',6,40);

一般に、ループ開始位置は AnalysisPoint ブロックの Location プロパティで指定されます。単一チャネルの解析ポイントの場合、ブロック名が既定の位置名として使用されます。マルチチャネルの解析ポイントの場合は、ブロック名にインデックスを付加したものが既定の位置名になります。

AP = AnalysisPoint('Y',2);  % two-channel analysis point
AP.Location

ans = 2×1 cell
    {'Y(1)'}
    {'Y(2)'}

既定の位置名はオーバーライドが可能で、Location プロパティを変更してより記述的な名前を使用できます。

% Rename loop opening locations to "InnerLoop" and "OuterLoop".
AP.Location = {'InnerLoop' ; 'OuterLoop'};
AP.Location

ans = 2×1 cell
    {'InnerLoop'}
    {'OuterLoop'}

参考

AnalysisPoint

トピック

一般化モデル
調整可能な係数をもつモデル
制御システムの解析と設計における対象信号のマーク (Simulink Control Design)