ldpcDecode

バイナリ LDPC 符号の復号化

R2021b 以降

構文

[Y,actualnumiter,finalparitychecks] = ldpcDecode(llr,decodercfg,maxnumiter)

[Y,actualnumiter,finalparitychecks] = ldpcDecode(llr,decodercfg,maxnumiter,Name=Value)

説明

[Y,actualnumiter,finalparitychecks] = ldpcDecode(llr,decodercfg,maxnumiter) は、入力 ldpcDecoderConfig 構成オブジェクト decodercfg で指定された LDPC 行列を使用して、入力対数尤度比 (LLR) llr を復号化します。正の LLR は、対応するビットがゼロである可能性が高いことを示します。入力 maxnumiter で指定された反復の最大数以内ですべてのパリティ チェックが満たされると、復号化は終了します。LDPC 符号は、スパース パリティ チェック行列およびシャノン限界に近いパフォーマンスを達成できる長いブロック長をもつ、線形の誤り制御符号です。

[Y,actualnumiter,finalparitychecks] = ldpcDecode(llr,decodercfg,maxnumiter,Name=Value) は、追加の名前と値の引数を指定します。たとえば、DecisionType='soft' は、軟判定復号化を指定し、LLR を出力します。

例

QAM 信号の符号化率 3/4 の LDPC コードワードの復号化

IEEE® 802.11 で指定された符号化率 3/4 の LDPC 符号を構成するために、プロトタイプ行列とブロック サイズのパラメーターを初期化します。関数 ldpcQuasiCyclicMatrix を使用して、パリティチェック行列を作成します。

P = [
    16 17 22 24  9  3 14 -1  4  2  7 -1 26 -1  2 -1 21 -1  1  0 -1 -1 -1 -1
    25 12 12  3  3 26  6 21 -1 15 22 -1 15 -1  4 -1 -1 16 -1  0  0 -1 -1 -1
    25 18 26 16 22 23  9 -1  0 -1  4 -1  4 -1  8 23 11 -1 -1 -1  0  0 -1 -1
     9  7  0  1 17 -1 -1  7  3 -1  3 23 -1 16 -1 -1 21 -1  0 -1 -1  0  0 -1
    24  5 26  7  1 -1 -1 15 24 15 -1  8 -1 13 -1 13 -1 11 -1 -1 -1 -1  0  0
     2  2 19 14 24  1 15 19 -1 21 -1  2 -1 24 -1  3 -1  2  1 -1 -1 -1 -1  0
    ];
blockSize = 27;
pcmatrix = ldpcQuasiCyclicMatrix(blockSize,P);

LDPC 符号化器と LDPC 復号化器の構成オブジェクトを作成し、それらのプロパティを表示します。

cfgLDPCEnc = ldpcEncoderConfig(pcmatrix)

cfgLDPCEnc = 
  ldpcEncoderConfig with properties:

     ParityCheckMatrix: [162×648 logical]

   Read-only properties:
           BlockLength: 648
    NumInformationBits: 486
    NumParityCheckBits: 162
              CodeRate: 0.7500

cfgLDPCDec = ldpcDecoderConfig(pcmatrix)

cfgLDPCDec = 
  ldpcDecoderConfig with properties:

     ParityCheckMatrix: [162×648 logical]
             Algorithm: 'bp'

   Read-only properties:
           BlockLength: 648
    NumInformationBits: 486
    NumParityCheckBits: 162
              CodeRate: 0.7500

LDPC 符号化され、M-QAM 変調されたビット ストリームを AWGN チャネル経由で送信します。信号を復調し、受信コードワードを復号化してから、ビット エラーをカウントします。for ループを使用し、送信データの LDPC 前方誤り訂正 (FEC) 符号化がある場合とない場合について、複数の SNR 設定を処理します。

M = 64;
maxnumiter = 10;
snr = [0.5 1 1.5 2];
numframes = 20000;

for ii = 1:length(snr)
    data = randi([0 1],cfgLDPCEnc.NumInformationBits,numframes,'int8');

    % Transmit and receive with LDPC coding
    encodedData = ldpcEncode(data,cfgLDPCEnc);
    modSignal = qammod(encodedData,M,InputType='bit');
    [rxsig, noisevar] = awgn(modSignal,snr(ii));
    llrOut = qamdemod(rxsig,M, ...
        OutputType='approxllr', ... % Or use 'llr' for exact but slower LLR calculation
        NoiseVariance=noisevar);
    rxbits = ldpcDecode(llrOut,cfgLDPCDec,maxnumiter);
    fprintf(['SNR = %2.1f\n   Coded: Error rate = %1.6f, ' ...
        'Number of errors = %d\n'], ...
        snr(ii),nnz(data~=rxbits)/numel(data),nnz(data~=rxbits));

    % Transmit and receive with no LDPC coding
    noCoding = qammod(data,M,InputType='bit');
    rxNoCoding = awgn(noCoding,snr(ii));
    rxBitsNoCoding = qamdemod(rxNoCoding,M,OutputType='bit');

    fprintf(['Noncoded: Error rate = %1.6f, ' ...
        'Number of errors = %d\n\n'], ...
        nnz(data~=rxBitsNoCoding)/numel(data),nnz(data~=rxBitsNoCoding))
end

SNR = 0.5
   Coded: Error rate = 0.000441, Number of errors = 4282

Noncoded: Error rate = 0.039045, Number of errors = 379515

SNR = 1.0
   Coded: Error rate = 0.000062, Number of errors = 604

Noncoded: Error rate = 0.032813, Number of errors = 318941

SNR = 1.5
   Coded: Error rate = 0.000003, Number of errors = 27

Noncoded: Error rate = 0.027001, Number of errors = 262450

SNR = 2.0
   Coded: Error rate = 0.000000, Number of errors = 0

Noncoded: Error rate = 0.021778, Number of errors = 211686

符号化率 3/4 の LDPC コードワードの復号化

IEEE® 802.11 で指定された符号化率 3/4 の LDPC 符号を構成するために、プロトタイプ行列とブロック サイズのパラメーターを初期化します。関数 ldpcQuasiCyclicMatrix を使用して、パリティチェック行列を作成します。

P = [
    16 17 22 24  9  3 14 -1  4  2  7 -1 26 -1  2 -1 21 -1  1  0 -1 -1 -1 -1
    25 12 12  3  3 26  6 21 -1 15 22 -1 15 -1  4 -1 -1 16 -1  0  0 -1 -1 -1
    25 18 26 16 22 23  9 -1  0 -1  4 -1  4 -1  8 23 11 -1 -1 -1  0  0 -1 -1
     9  7  0  1 17 -1 -1  7  3 -1  3 23 -1 16 -1 -1 21 -1  0 -1 -1  0  0 -1
    24  5 26  7  1 -1 -1 15 24 15 -1  8 -1 13 -1 13 -1 11 -1 -1 -1 -1  0  0
     2  2 19 14 24  1 15 19 -1 21 -1  2 -1 24 -1  3 -1  2  1 -1 -1 -1 -1  0
    ];
blockSize = 27;
pcmatrix = ldpcQuasiCyclicMatrix(blockSize,P);

LDPC 符号化器と LDPC 復号化器の構成オブジェクトを作成し、それらのプロパティを表示します。

cfgLDPCEnc = ldpcEncoderConfig(pcmatrix)

cfgLDPCEnc = 
  ldpcEncoderConfig with properties:

     ParityCheckMatrix: [162×648 logical]

   Read-only properties:
           BlockLength: 648
    NumInformationBits: 486
    NumParityCheckBits: 162
              CodeRate: 0.7500

cfgLDPCDec = ldpcDecoderConfig(pcmatrix)

cfgLDPCDec = 
  ldpcDecoderConfig with properties:

     ParityCheckMatrix: [162×648 logical]
             Algorithm: 'bp'

   Read-only properties:
           BlockLength: 648
    NumInformationBits: 486
    NumParityCheckBits: 162
              CodeRate: 0.7500

LDPC 符号化され、QPSK 変調されたビット ストリームを AWGN チャネル経由で送信します。信号を復調し、受信コードワードを復号化してから、ビット エラーをカウントします。入れ子の for ループを使用し、複数の SNR 設定、および送信データの LDPC 前方誤り訂正 (FEC) 符号化がある場合とない場合のフレームについて処理します。

M = 4;
maxnumiter = 10;
snr = [3 6 20];
numframes = 10;

ber = comm.ErrorRate;
ber2 = comm.ErrorRate;

for ii = 1:length(snr)
    for counter = 1:numframes
        data = randi([0 1],cfgLDPCEnc.NumInformationBits,1,'int8');
        % Transmit and receive with LDPC coding
        encodedData = ldpcEncode(data,cfgLDPCEnc);
        modSignal = pskmod(encodedData,M,InputType='bit');
        [rxsig, noisevar] = awgn(modSignal,snr(ii));
        demodSignal = pskdemod(rxsig,M, ...
            OutputType='approxllr', ...
            NoiseVariance=noisevar);
        rxbits = ldpcDecode(demodSignal,cfgLDPCDec,maxnumiter);
        errStats = ber(data,rxbits);
        % Transmit and receive with no LDPC coding
        noCoding = pskmod(data,M,InputType='bit');
        rxNoCoding = awgn(noCoding,snr(ii));
        rxBitsNoCoding = pskdemod(rxNoCoding,M,OutputType='bit');
        errStatsNoCoding = ber2(data,int8(rxBitsNoCoding));
    end
    fprintf(['SNR = %2d\n   Coded: Error rate = %1.2f, ' ...
        'Number of errors = %d\n'], ...
        snr(ii),errStats(1),errStats(2))
    fprintf(['Noncoded: Error rate = %1.2f, ' ...
        'Number of errors = %d\n'], ...
        errStatsNoCoding(1),errStatsNoCoding(2))
    reset(ber);
    reset(ber2);
end

SNR =  3
   Coded: Error rate = 0.07, Number of errors = 355

Noncoded: Error rate = 0.08, Number of errors = 384

SNR =  6
   Coded: Error rate = 0.00, Number of errors = 0

Noncoded: Error rate = 0.02, Number of errors = 98

SNR = 20
   Coded: Error rate = 0.00, Number of errors = 0

Noncoded: Error rate = 0.00, Number of errors = 0

GPU を使用した LDPC 復号化

GPU を使用して、LDPC 符号化、PSK 変調、AWGN チャネル モデリング、PSK 復調、LDPC 復号化、およびビット エラー レートの計算を高速化します。この例では、確率伝播復号化アルゴリズムおよび正規化 min-sum 復号化アルゴリズムの誤り統計を計算します。

LDPC 構成オブジェクトの作成

LDPC 符号化器構成オブジェクトおよび LDPC 復号化器構成オブジェクトを作成します。シミュレーション変数を定義します。

% Use ldpcQuasiCyclicMatrix to create a parity-check matrix
load("LDPCExamplePrototypeMatrix.mat","P"); % A prototype matrix from the 5G standard
blockSize = 384;
H = ldpcQuasiCyclicMatrix(blockSize, P);
encoderCfg = ldpcEncoderConfig(H);
decoderCfg1 = ldpcDecoderConfig(encoderCfg); % The default algorithm is "bp"
decoderCfg2 = ldpcDecoderConfig(encoderCfg,"norm-min-sum");

M = 4; % Modulation order (QPSK)
snr = [-2 -1.5 -1];
numFramesPerCall = 50;
numCalls = 40;
maxNumIter = 20;
s = rng(1235); % Fix random seed
errRate = zeros(length(snr),2);

ビット エラー レートの計算

gpuArray (Parallel Computing Toolbox)オブジェクトにランダム ビットを生成し、そのデータを ldpcEncode、pskmod、awgn、pskdemod、ldpcDecode、および biterr 各関数に順に渡します。各 SNR 設定に対して、確率伝播復号化アルゴリズムおよび正規化 min-sum 復号化アルゴリズムの誤り統計を計算します。

for ii = 1:length(snr)
    ttlErr = [0 0];
    noiseVariance = 1/10^(snr(ii)/10);
    for counter = 1:numCalls
        data = gpuArray.randi([0 1],encoderCfg.NumInformationBits,numFramesPerCall,'logical');

        % Transmit and receive LDPC coded signal data
        encData = ldpcEncode(data,encoderCfg);
        modSig = pskmod(encData,M,pi/4,'InputType','bit');
        rxSig = awgn(modSig,snr(ii)); % Signal power = 0 dBW
        demodSig = pskdemod(rxSig,M,pi/4,...
            'OutputType','approxllr','NoiseVariance',noiseVariance);

        % Decode and update number of bit errors

        % Using bp
        rxBits1 = ldpcDecode(demodSig,decoderCfg1,maxNumIter);
        numErr1 = biterr(data,rxBits1);

        % Using norm-min-sum
        rxBits2 = ldpcDecode(demodSig,decoderCfg2,maxNumIter);
        numErr2 = biterr(data,rxBits2);

        ttlErr = ttlErr + [numErr1 numErr2];
    end
    ttlBits = numCalls*numel(rxBits1);
    
    errRate(ii,:) = ttlErr/ttlBits;
end

ビット エラー レートの比較

誤り統計をプロットします。確率伝播アルゴリズムのビット エラー レートは、正規化 min-sum アルゴリズムよりもわずかに低くなることが予想されます。

plot(snr,errRate,'-x')
grid on
legend('bp','norm-min-sum')
xlabel('SNR (dB)')
ylabel('BER')

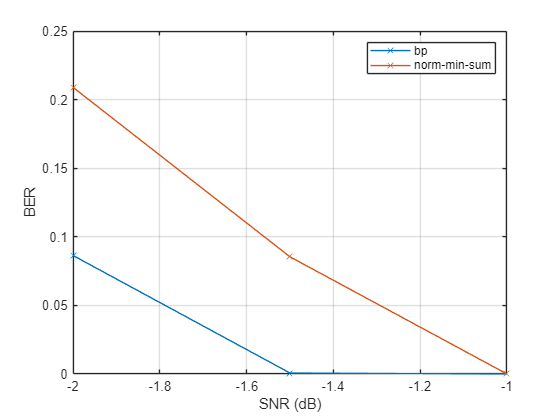
速度の比較

4 つの場合について実行時間を比較します。既定では、ldpcDecode はすべてのパリティ チェックが満たされた後に復号化を終了します。

% Use belief propagation algorithm on CPU, without multithreading
demodSigCPU = gather(demodSig);
tic
[rxBitsCPU1,actualNumIterCPU1,finalParityChecksCPU1] = ...
    ldpcDecode(demodSigCPU,decoderCfg1,maxNumIter,'Multithreaded',false);
toc

Elapsed time is 4.270400 seconds.

% Use belief propagation algorithm on CPU, with multithreading
tic
[rxBitsCPU2,actualNumIterCPU2,finalParityChecksCPU2] = ...
    ldpcDecode(demodSigCPU,decoderCfg1,maxNumIter);
toc

Elapsed time is 1.069500 seconds.

% Use belief propagation algorithm on GPU
tic
[rxBits1,actualNumIter1,finalParityChecks1] = ...
    ldpcDecode(demodSig,decoderCfg1,maxNumIter);
toc

Elapsed time is 2.117112 seconds.

% Use normalized min-sum algorithm on GPU
tic
[rxBits2,actualNumIter2,finalParityChecks2] = ...
    ldpcDecode(demodSig,decoderCfg2,maxNumIter);
toc

Elapsed time is 0.615488 seconds.

オプションの復号化器出力の確認

SNR が十分高い場合は、確率伝播アルゴリズムよりも正規化 min-sum アルゴリズムの方が少ない反復回数で済むことを確認します。

length(find(actualNumIter2 < actualNumIter1))

ans = 
50

length(find(actualNumIter2 == actualNumIter1))

ans = 
0

指定した最大反復回数よりも実際に実行された反復回数の方が少ない場合、最終的なパリティ チェックの結果がすべてゼロになることを確認します。

nnz(finalParityChecks1(:,actualNumIter1<maxNumIter))

ans = 
0

nnz(finalParityChecks2(:,actualNumIter2<maxNumIter))

ans = 
0

乱数発生器の状態を復元します。

rng(s);

入力引数

llr — 対数尤度比

行列

対数尤度比。入力 decodercfg の BlockLength プロパティと等しい行数をもつ行列として指定します。llr の各列は、1 つのコードワードに対応します。関数は各列を個別に復号化します。正の LLR は、対応するビットがゼロである可能性が高いことを示します。

データ型: double | single

decodercfg — LDPC 復号化器の構成

ldpcDecoderConfig オブジェクト

LDPC 復号化器の構成。ldpcDecoderConfig オブジェクトとして指定します。

maxnumiter — 復号化反復の最大数

正のスカラー

復号化反復の最大数。正のスカラーとして指定します。

データ型: double

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

例: Termination='max'

OutputFormat — 出力形式

'info' (既定値) | 'whole'

出力形式。以下のいずれかの値として指定します。

• 'info' — 復号化された情報ビットのみを出力します。関数が出力する行数は、入力 decodercfg の NumInformationBits プロパティと同じになります。

• 'whole' — 情報ビットとパリティチェック ビットを含む、復号化された LDPC コードワード ビットすべてを出力します。関数が出力する行数は、入力 decodercfg の BlockLength プロパティと同じになります。

DecisionType — Decision type

'hard' (既定値) | 'soft'

LDPC 復号化の判定タイプ。次のいずれかの値として指定します。

• 'hard' — 硬判定復号化を実行し、復号化されたビットを int8 データ型の値として出力します。

• 'soft' — 軟判定復号化を実行し、入力と同じデータ型で LLR を出力します。

MinSumScalingFactor — 正規化された min-sum 復号化アルゴリズムのスケーリング係数

0.75 (既定値) | 範囲 (0, 1] のスカラー

正規化された min-sum 復号化アルゴリズムのスケーリング係数。範囲 (0, 1] のスカラーとして指定します。詳細については、正規化された min-sum 復号化を参照してください。

依存関係

このプロパティを有効にするには、入力 decodercfg の Algorithm プロパティを 'norm-min-sum' に設定します。

MinSumOffset — min-sum 復号化アルゴリズムのオフセット

0.5 (既定値) | スカラー

min-sum 復号化アルゴリズムのオフセット。スカラーとして指定します。詳細については、オフセット min-sum 復号化を参照してください。

依存関係

このプロパティを有効にするには、入力 decodercfg の Algorithm プロパティを 'offset-min-sum' に設定します。

Termination — 復号化終了基準

'early' (既定値) | 'max'

復号化終了基準。次のいずれかの値として指定します。

• 'early' — 入力 maxnumiter で指定された反復の最大数以内ですべてのパリティ チェックが満たされると、復号化の反復を終了します。

• 'max' — 最大数 maxnumiter の反復が完了したときに復号化を終了します。

Multithreaded — CPU 上でのマルチスレッド実行の有効化

true または 1 (既定値) | false または 0

CPU 上でのマルチスレッド実行の有効化。logical 1 (true) または logical 0 (false) として指定します。インタープリター モードで MATLAB^® を実行し、この引数を true に設定すると、関数は複数のスレッドで復号化アルゴリズムを実行します。この関数は、入力の decodercfg オブジェクトにおいて NumRowsPerLayer = 1 である場合にマルチスレッド実行をオフにします。

ヒント

• 大きなパリティチェック行列では、マルチスレッド実行により、LDPC 復号化の処理時間が大幅に短縮されます。

依存関係

このプロパティを有効にするには、CPU 上で MATLAB をインタープリター モードで実行します。

出力引数

Y — 復号化されたコードワード

行列

復号化されたコードワード。llr(1:K,:) の復号化されたビットを表す K 行の行列として返されます。K は、入力 decodercfg の NumInformationBits プロパティと同じです。復号化操作の場合、llr の各列は 1 つのコードワードに対応します。関数は各列を個別に復号化します。名前と値の引数 OutputFormat は、出力に復号化された情報ビットを含める (既定) か、LDPC コードワード ビット全体を含めるかを指定します。名前と値の引数 DecisionType は、復号化判定タイプとこの出力のデータ型を指定して判定します。

詳細については、アルゴリズムを参照してください。

データ型: int8 | double | single

actualnumiter — 復号化の実際の反復回数

行ベクトル

復号化の実際の反復回数。行ベクトルとして返されます。コードワードのすべてのパリティ チェックが満たされると、反復の最大数 maxnumiter に達する前でも復号化が停止することがあります。この出力は、関数がコードワードに対して実行した実際の反復回数から成る行ベクトルです。

データ型: double

finalparitychecks — 各コードワードに対する最終パリティ チェック

行列

各コードワードに対する最終パリティ チェック。入力 decodercfg の ParityCheckBits プロパティと等しい行数をもつ行列として返されます。復号化操作の場合、この出力の各列は、対応するコードワードに対する最終パリティ チェックになります。

データ型: double

アルゴリズム

以下のメッセージ伝達アルゴリズムのいずれかを使用する LDPC 復号化。

確率伝播復号化

確率伝播アルゴリズムの実装は、Gallager によって提示された復号化アルゴリズムに基づいています [2]。

LDPC 符号化されて送信されたコードワード c = c₀、c₁、...、c_n-1 に対して、LDPC 復号化器への入力は、対数尤度比 (LLR) の値 $$L(c_i)=\log \left(\frac{\mathrm{Pr}(c_i=0|\text{channel output for }{c}_i)}{\mathrm{Pr}(c_i=1|\text{channel output for }{c}_i)}\right)$$ になります。

各反復で、アルゴリズムの主なコンポーネントが以下の式に基づいて更新されます。

$$L(r_{ji})=2\text{atanh}\left({\displaystyle \prod _{i^{\prime }\in V_j\backslash i}\tanh \left(\frac{1}{2}L(q_{i^{\prime }j})\right)}\right)$$,

$$L(q_{ij})=L(c_i)+{\displaystyle \sum _{j^{\prime }\in C_i\backslash j}L(r_{j^{\prime }i})}$$ (最初の反復の前に $$L(q_{ij})=L(c_i)$$ として初期化される)、および

$$L(Q_i)=L(c_i)+{\displaystyle \sum _{j^{\prime }\in C_i}L(r_{j^{\prime }i})}$$.

それぞれの反復の最後で、L(Q_i) には、送信ビット c_i に対する LLR 値の更新された推定値が含まれます。値 L(Q_i) は c_i の軟判定出力です。L(Q_i) ≤ 0 の場合、c_i の硬判定出力は 1 です。それ以外の場合、c_i の硬判定出力は 0 です。

すべてのパリティ チェックが満たされた場合に停止するように復号化が設定されている場合、アルゴリズムは、各反復の終わりにパリティ チェック式 (H c' = 0) を検証します。すべてのパリティ チェックが満たされた場合、または最大反復回数に到達した場合、復号化は停止します。

インデックス集合 $$C_i\backslash j$$ と $$V_j\backslash i$$ は、パリティ チェック行列 (PCM) に基づいています。インデックス集合 C_i と V_j はそれぞれ、PCM の列 i と行 j のすべての非ゼロ要素に対応します。

次の図は、与えられた PCM の i = 5 と j = 3 に対するインデックス集合の計算を示しています。

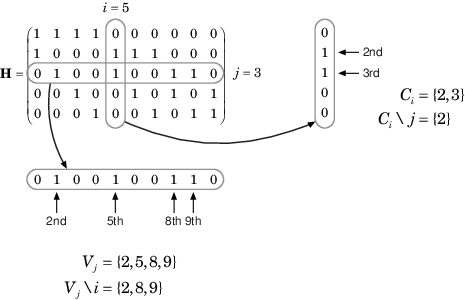
無限数がアルゴリズム式で使用されないように、atanh(1) は 19.07 に、atanh(–1) は –19.07 に設定されます。有限値で演算を行うために、MATLAB は tanh(19.07) に対して 1 を、tanh(-19.07) に対して –1 を返します。

階層的確率伝播復号化

階層的確率伝播アルゴリズムの実装は、Hocevar [3] の II.A 節にある復号化アルゴリズムに基づいています。復号化ループは、PCM の行 (層) のサブセットを反復します。レイヤー内の各行 m と各ビット インデックス j について、実装ではアルゴリズムの主なコンポーネントが以下の式に基づいて更新されます。

(1) $$L(q_{mj})=L(q_j)-R_{mj}$$,

(2) $$A_{mj}={\displaystyle \sum _{\begin{array}{c}n \in N\left(m\right)\\ n\ne j\end{array}}\text{ψ}(L(q_{mn}))}$$,

(3) $$s_{mj}={\displaystyle \prod _{\begin{array}{c}n \in N\left(m\right)\\ n\ne j\end{array}}\text{sign}(L(q_{mn}))}$$,

(4) $$R_{mj}=-s_{mj}\text{ψ}(A_{mj})$$、および

(5) $$L(q_j)=L(q_{mj})+R_{mj}$$.

各レイヤーについて、復号化の式 (5) が、現在の LLR 入力 $$L(q_{mj})$$ と前のレイヤーの更新 $$R_{mj}$$ から得られる結合された入力に対して適用されます。

ノードのサブセットのみがレイヤーで更新されるため、階層的確率伝播アルゴリズムは、確率伝播アルゴリズムと比較して高速です。階層的確率伝播アルゴリズムを使用すれば、確率伝播復号化が達成するのと同じエラー レートを達成するために使用する復号化反復回数が半分で済みます。

正規化された min-sum 復号化

正規化された min-sum 復号化アルゴリズムの実装は、式 (2) を次のように置き換えた階層的確率伝播アルゴリズムに従います。

$$A_{mj}=\underset{\begin{array}{c}n \in N\left(m\right)\\ n\ne j\end{array}}{\min }(\left|L(q_{mn}) \right|\cdot \alpha )$$,

ここで、α は、関数 ldpcDecode への入力引数 MinSumScalingFactor で指定される、範囲 (0, 1] のスケーリング係数です。この式は、Chen [4] にある式 (4) を応用したものです。

オフセット min-sum 復号化

オフセット min-sum 復号化アルゴリズムの実装は、式 (2) を次のように置き換えた階層的確率伝播アルゴリズムに従います。

$$A_{mj} = \max (\underset{\begin{array}{c}n \in N\left(m\right)\\ n\ne j\end{array}}{\min } (\left|L\left(q_{mn}\right)\right|- \beta ), 0)$$,

ここで、β は、0 以上のオフセットで、関数 ldpcDecode への入力引数 MinSumOffset で指定されます。この式は、Chen [4] にある式 (5) を応用したものです。

参照

[1] IEEE^® Std 802.11™-2020 (Revision of IEEE Std 802.11-2016). "Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications." IEEE Standard for Information technology — Telecommunications and information exchange between systems. Local and metropolitan area networks — Specific requirements.

[2] Gallager, Robert G. Low-Density Parity-Check Codes. Cambridge, MA: MIT Press, 1963.

[3] Hocevar, D.E. "A reduced complexity decoder architecture via layered decoding of LDPC codes." In IEEE Workshop on Signal Processing Systems, 2004. SIPS 2004, 107-112. https://doi.org/10.1109/SIPS.2004.1363033.

[4] Chen, Jinghu, R.M. Tanner, C. Jones, and Yan Li. "Improved min-sum decoding algorithms for irregular LDPC codes." In Proceedings. International Symposium on Information Theory, 2005. ISIT 2005. https://doi.org/10.1109/ISIT.2005.1523374.

拡張機能

C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

この関数は、GPU 配列の入力をサポートします。詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

メモ

CPU プロセッサと GPU プロセッサを比較した場合、BP 復号化アルゴリズムと階層的 BP 復号化アルゴリズムの軟判定出力がわずかに異なる場合があります。この差は、2 つのプロセッサにおける数値演算の順序によるものです。ビット エラー レートなどのシステムレベルのメトリクスは、十分な数の信号サンプルを処理することで収束します。

バージョン履歴

R2021b で導入

R2023b: gpuArray のサポートの追加

関数 ldpcDecode において、グラフィックス処理装置 (GPU) でコードを実行するための gpuArray (Parallel Computing Toolbox) オブジェクト処理のサポートが追加されました。GPU を搭載しているコンピューターでは、llr の入力が gpuArray の場合、この関数は、Y および finalparitychecks を gpuArray オブジェクトとして出力し、actualnumiter を CPU 上の数値配列として出力します。

R2023b: single データ型のサポート

関数 ldpcDecode において、single データ型信号入力のサポートが追加されました。入力信号が single 型だった場合、この関数による計算は単精度でネイティブに行われ、返される出力も single 型になります。

R2023b より前では、データ型が single である入力信号が double にキャストされ、この関数によって倍精度でネイティブに計算が行われ、出力時に元の single にキャストされていました。

R2023b の出力は、以前のリリースと比べてわずかに異なる場合があります。R2023b と以前のリリースの結果を比べると、ネイティブな単精度の計算と倍精度の計算の丸めの違いに起因するわずかな差異が生じる可能性があります。

参考

関数

• ldpcEncode | ldpcQuasiCyclicMatrix

オブジェクト

• ldpcDecoderConfig | ldpcEncoderConfig