Main Content

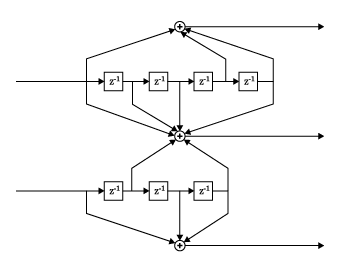
distspec

畳み込み符号の距離スペクトルの計算

ページ内をすべて折りたたむ

構文

spect = distspec(trellis,numcomp)

説明

例

spect = distspec(trellis,numcomp) が計算するのは、自由距離と、線形畳み込み符号の重みおよび距離スペクトルの成分が要求された数です。畳み込み符号はブロック境界をもたないため、重みスペクトルおよび距離スペクトルは半無限で、最初の数成分で適切に近似されます。

例

すべて折りたたむ

ライブ スクリプトを開く

関数 distspec を使用して、符号化率 2/3 の畳み込み符号の距離スペクトルを計算します。出力される距離スペクトルを関数bercodingへの入力として使用し、この符号を同期 BPSK 変調で使用するシステムのビット エラー レートの理論的な上限値を求めます。関数berfitを使用して上限値をプロットします。

この図は、2 つの入力ストリーム、3 つの出力ストリーム、および 2 つのシフト レジスタがある符号化率 2/3 の符号化器を示しています。

この符号化器を表すトレリス構造体を作成します。上のパスの拘束長は 5、下のパスの拘束長は 4 に設定します。符号生成行列の 8 進数表現は、上と下のシフト レジスタからのタップに対応します。トレリス構造体は、関数 distspec への符号化率 2/3 の畳み込み符号を表す入力として使用できます。

trellis = poly2trellis([5 4],[23 35 0; 0 5 13])
trellis = struct with fields:
     numInputSymbols: 4
    numOutputSymbols: 8
           numStates: 128
          nextStates: [128x4 double]
             outputs: [128x4 double]


spect = distspec(trellis,4)
spect = struct with fields:
     dfree: 5
    weight: [1 6 28 142]
     event: [1 2 8 25]

関数 bercoding と距離スペクトル構造体を使用し、この符号を同期 BPSK 変調で使用するシステムのビット エラー レートの理論的な上限値を求めます。関数 berfit を使用して上限値をプロットします。

berub = bercoding(1:10,'conv','hard',2/3,spect);  % BER upper bound
berfit(1:10,berub); ylabel('Upper Bound on BER'); % Plot

入力引数

すべて折りたたむ

トレリス表現。符号化率 K/N の符号に対するトレリス表現を含む MATLAB® 構造体として指定します。K は入力ビット ストリーム数を表し、N は出力ビット ストリーム数を表します。

トレリス構造体には次のフィールドがあります。トレリス構造体は、関数 poly2trellis を使用して作成するか、手動で作成することができます。この構造体の詳細については、畳み込み符号のトレリス表現および関数 istrellis を参照してください。

符号化器への入力シンボルの数。2K と等しい整数として指定します。ここで、K は入力ビット ストリームの数です。

符号化器からの出力シンボルの数。2N と等しい整数として指定します。ここで、N は出力ビット ストリームの数です。

符号化器内の状態の数。2 のべき乗として指定します。

現在の状態と現在の入力のすべての組み合わせの次の状態。整数の行列として指定します。行列のサイズは numStates 行 2K 列でなければなりません。

現在の状態と現在の入力のすべての組み合わせの出力。8 進数の行列として指定します。行列のサイズは numStates 行 2K 列でなければなりません。

データ型: struct

計算する線形畳み込み符号の重みと距離スペクトルの成分の要求された数。正の整数として指定します。

データ型: double

出力引数

すべて折りたたむ

距離スペクトル。次のフィールドを含む構造体として返されます。

フィールド平均
spect.dfreeコードの自由距離。これは誤りイベントを作成するために必要な符号化シーケンスの最小誤り数です。
spect.weightspect.event に列挙されるエラー イベントの情報ビット エラーの総数をリストする長さ n のベクトル。
spect.eventspect.dfree と spect.dfree+n-1 の間の各距離の誤りイベントの数をリストする長さ n のベクトル。ベクトルは距離スペクトルの最初の n 成分を表します。

アルゴリズム

[2]に説明されているように、関数はスタックで実装されるツリー型探索アルゴリズムを使用します。

参照

[1] Bocharova, I.E., and B.D. Kudryashov. “Rational Rate Punctured Convolutional Codes for Soft-Decision Viterbi Decoding.” IEEE Transactions on Information Theory 43, no. 4 (July 1997): 1305–13. https://doi.org/10.1109/18.605600.

[2] Cedervall, M.L., and R. Johannesson. “A Fast Algorithm for Computing Distance Spectrum of Convolutional Codes.” IEEE Transactions on Information Theory 35, no. 6 (November 1989): 1146–59. https://doi.org/10.1109/18.45271.

[3] Chang J., D. Hwang, and M. Lin. “Some Extended Results on the Search for Good Convolutional Codes.” IEEE Transactions on Information Theory 43, no. 5 (September 1997): 1682–97. https://doi.org/10.1109/18.623175.

[4] Frenger, P.K., P. Orten, and T. Ottosson. “Comments and Additions to Recent Papers on New Convolutional Codes.” IEEE Transactions on Information Theory 47, no. 3 (March 2001): 1199–1201. https://doi.org/10.1109/18.915683.

バージョン履歴

R2006a より前に導入

参考

関数