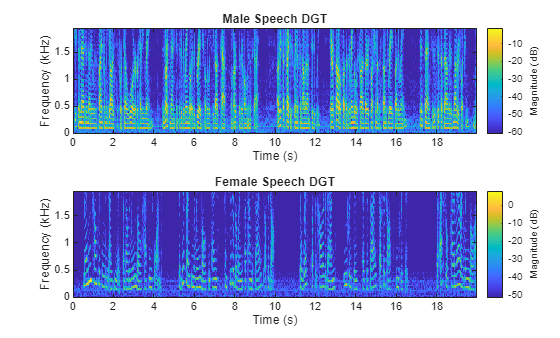
時間-周波数解析

CWT、定 Q 変換、経験的モード分解、ウェーブレットコヒーレンス、ウェーブレットクロススペクトル

連続ウェーブレット変換 (CWT) を使用して、信号の周波数成分が時間の経過と共に変化する様子を解析できます。非定常ガボールフレームと定 Q 変換 (CQT) を使用して、適応時間-周波数解析を実行できます。2 つの信号について、ウェーブレットコヒーレンスは共通する時変パターンを明らかにします。非線形および非定常過程のデータ適応時間-周波数解析を実行できます。イメージに対しては、連続ウェーブレット解析はイメージの周波数成分がイメージ全体でどのように変化するかを示し、ノイズを含むイメージのパターンを明らかにするのに役立ちます。よりシャープな解像度を得て、信号から振動モードを抽出するために、ウェーブレットシンクロスクイージングを使用できます。

Wavelet Toolbox™ を使用して、信号とイメージの時間-周波数解析を実行します。CQT では、広い帯域成分に対しては多くの周波数サンプルを、狭い帯域成分に対しては少ない周波数サンプルを使用して、帯域幅を別個にサンプリングすることができます。CWT を使用すると、2 つの信号間のウェーブレットコヒーレンスを得ることができます。非線形または非定常過程を固有の振動モードに分解することができます。また、時間-周波数局在型の Approximation を信号に再構成することもできます。特定の周波数または周期範囲を持つ CWT フィルターバンクを作成し、そのフィルターバンクを複数の信号に効率的に適用することができます。時間と周波数のウェーブレットを可視化できます。

主要なトピック

注目の例

Practical Introduction to Time-Frequency Analysis Using the Continuous Wavelet Transform

Perform and interpret time-frequency analysis of signals using the continuous wavelet transform.

ライブスクリプトを開く

時間-周波数解析と連続ウェーブレット変換

CWT によってシャープな時間-周波数表現が得られることを学習します。

ライブスクリプトを開く

Using Wavelet Time-Frequency Analyzer App

Learn how to use to visualize scalograms of 1-D signals and recreate results in your workspace.

ライブスクリプトを開く

時変コヒーレンス

フーリエ領域コヒーレンスは、周波数の関数として、2 つの定常過程間の線形相関を 0 から 1 のスケールで測定するための確立された手法です。ウェーブレットでは、データについての、時間とスケール (周波数) での局所情報が提供されるため、ウェーブレットベースのコヒーレンスを使用すると、周波数の関数として時変相関を測定できます。つまり、非定常過程に適したコヒーレンス測定というわけです。

ライブスクリプトを開く

ウェーブレットコヒーレンスを使用した信号の時間-周波数成分の比較

この例では、ウェーブレットコヒーレンスとウェーブレットクロススペクトルを使用して、2 つの時系列における時間局在型の共通の振動動作を識別する方法を示します。また、この例では、ウェーブレットコヒーレンスとウェーブレットクロススペクトルを、対応するフーリエコヒーレンスとフーリエクロススペクトルと比較します。mscohere (Signal Processing Toolbox)とcpsd (Signal Processing Toolbox)を使用してこれらの例を実行するには、Signal Processing Toolbox™ が必要です。

ライブスクリプトを開く

時間局在型の周波数成分の削除

指数的に重み付けされた正弦波で構成される信号を作成します。信号には 2 つの 25 Hz 成分があります。1 つは 0.2 秒を中心とし、もう 1 つは 0.5 秒を中心とします。70 Hz 成分も 2 つあります。1 つは 0.2 秒を中心とし、もう 1 つは 0.8 秒を中心とします。最初の 25 Hz 成分と 70 Hz 成分は同時に発生します。

ライブスクリプトを開く