非定常ガボールフレームと定 Q 変換

非定常ガボールフレームを使用すると、信号の時間適応解析または周波数適応解析を実施できます。関数 cqt および icqt は、非定常ガボールフレームを使用して信号の定 Q (周波数適応) 変換 (CQT) を求めます。非定常ガボールフレームの重要な強みは、安定した逆変換の構成が有効になり、完全再構成を生成できるということです。

非定常ガボール変換 (NSGT) の理論は、Jailet [1]と Balazs、Dörfler、Jaillet、Holighaus、および Velasco [2]によって発表されました。この理論により、FFT ベースの手法を使用した NGST の効率的な実装が可能になります。Dörfler、Holighaus、Grill、および Velasco[3]、[4]は、効率的な完全可逆 CQT のフレームワークを開発しました。[3]と[4]に記載されているアルゴリズムは、単純畳み込みで得られる同じ位相を保持しない、位相固定バージョンの CQT を実装します。[5] の中で、Schörkhuber、Klapuri、Holighaus、および Dörfler は、単純畳み込みによって得られる係数を再現する、CQT および逆 CQT の効率的なアルゴリズムを開発しています。The Large Time-Frequency Analysis Toolbox ([6]) は、非定常ガボール解析と合成のためのさまざまなアルゴリズムを提供します。

標準的なガボール解析では、固定サイズのウィンドウで時間-周波数平面がタイリングされます。非定常ガボールフレームは、時間-周波数平面のタイリングに使用されるさまざまなサイズのウィンドウ関数の集合です。ウェーブレット解析により、時間-周波数平面が同様にタイリングされます。サンプリング密度を時間または周波数で柔軟に変更できます。非定常ガボールフレームは、固定サイズの時間-周波数ウィンドウが最適ではない音声信号処理などの領域で役に立ちます。短時間フーリエ変換とは異なり、定 Q 変換で使用されるウィンドウには、適応性のある帯域幅およびサンプリング密度があります。周波数空間では、ウィンドウは対数的に等間隔の中心周波数を中心とします。

時間-周波数平面の分解

f(t) のフーリエ変換とは、f(t) と e^{j ω t} の相関です。

$F (ω) = \int_{- \infty}^{\infty} f (t) e^{- j ω t} d t .$

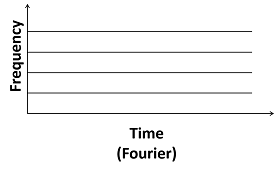
e^{j ω t} はコンパクトサポートを持たないため、フーリエ変換を非定常信号の調査に選択することは不適切です。信号の周波数成分が時間の経過と共に変化する場合、フーリエ変換は変化の内容や変化が発生するタイミングを捉えません。ここに示す時間-周波数平面の分割は、こうしたフーリエ変換の動作を表しています。

非定常信号 f(t) の時間-周波数解析を実行するには、次のようなウィンドウ関数 $g (t)$ を使用します。

偶数かつ実数値。
事実上、有限の間隔でのみ非ゼロになる。
ノルムが 1 に等しい。
$g (t)$ のフーリエ変換がゼロを中心とし、ローパスである。

ウィンドウ $g (t)$ を f(t) にスライドさせ、結果のフーリエ変換を求めます。

$S F (u, ζ) = \int f (t) g (t - u) e^{- j ζ t} d t .$

f(t) をガボールアトム $g (t - u) e^{j ζ t}$ と相関させることが標準的なガボール解析です。u を変化させることで、時刻 u 付近の f(t) の値のみを検討します。 $g (t)$ のサポートにより、時刻 u 付近の近傍のサイズが決まります。 $g_{u, ζ} (t) = g (t - u) e^{ζ t}$ のフーリエ変換は、 $g (t)$ のフーリエ変換の ζ による平行移動で、次によって与えられます。

${\hat{g}}_{u, ζ} (ω) = e^{- (ω - ζ)} \hat{g} (ω - ζ) .$

${\hat{g}}_{u, ζ} (ω)$ のエネルギー集中には分散 σ_ω があり、ζ を中心とします。ウィンドウ $g_{u, ζ} (t) = g (t - u) e^{ζ t}$ が規則的なグリッドでシフトする場合、シフトされたウィンドウと f(t) の積のフーリエ変換は短時間フーリエ変換 (STFT) です。時間-周波数平面の STFT タイリングは、それぞれが (u, ζ) を中心とするボックスのグリッドとして表すことができます。

関数の集合 ${g_{u, ζ}}$ は、"ガボールフレーム" として知られています。この集合の要素は、"ガボールアトム" と呼ばれます。フレームは、関数の集合 {h_k(t)} であり、以下の条件を満たします。任意の関数 f(t) で次のようになるように、定数 0 < A ≤ B < ∞ が存在します。

$A ‖ f ‖^{2} \leq Σ_{k} | 〈 f, h_{k} 〉 |^{2} \leq B ‖ f ‖^{2} .$

時間での $g (t)$ のエネルギー集中度には分散 σ_t があります。周波数での $\hat{g} (ω)$ のエネルギー集中度には分散 σ_ω があります。ウィンドウが時間および周波数的にどれだけ信号を局在化できるかは、エネルギー集中度によって決まります。時間と周波数の間の不確かさの原理によって、時間領域および周波数領域での局在化を同時に行う場合の精度には次で示される制限があります。

$σ_{t} σ_{ω} \geq \frac{1}{2} .$

一方の領域でウィンドウを狭めると、他方の領域では局在化が劣化します。 $g (t)$ がガウスの場合、ウィンドウの領域は最小限であることをガボールは示しました。

定 Q 変換

CQT では、帯域幅および周波数でのサンプリング密度は異なります。ウィンドウは構築され、周波数領域に直接適用されます。ウィンドウごとに中心周波数と帯域幅が異なりますが、帯域幅に対する中心周波数の比率は一定のままです。一定の比率を維持することは以下を意味します。

時間での分解能は高周波数で向上します。
周波数での分解能は低周波数で向上します。

不確かさの原理により、時間は、帯域幅に応じてウィンドウごとにシフトします。

CQT は以下に応じて異なります。

ウィンドウ関数 g_k は、実数値の偶関数です。周波数領域では、g_k のフーリエ変換は、区間 [-Fs/2, Fs/2] で定義されます。
サンプリングレート ζ_s。
オクターブあたりのビンの数 b。
最低周波数および最高周波数 ζ_min および ζ_max。

最小周波数 ζ_min およびオクターブあたりのビン数 b を選択します。次に、幾何学的に配置された周波数のシーケンスを形成します。

ζ_k = ζ_min × 2^k/b

k = 0,...,K について、K は、ζ_K がナイキスト周波数 ζ_s/2 より厳密に小さくなる最大周波数となるような整数です。k 番目の周波数での帯域幅は、Ω_k = ζ_k+1-ζ_k-1 に設定されます。このサンプリングの場合、そのウィンドウ帯域幅に対する k 番目の中心周波数の比率は、次のように k とは独立しています。

Q = ζ_k/Δ_k = (2^1/b-2^-1/b)^-1.

確実に完全再構成が行われるよう、DC 成分およびナイキスト周波数が、それぞれシーケンスの先頭および最後に追加されます。

W(ω) は、ウィンドウ関数 g_k を形成します。W(ω) は、0 を中心とし、区間 [-½,½] では正の数であり、それ以外では 0 である、実数の連続偶関数です。W(ω) は、各中心周波数 ζ_k に平行移動され、スケーリングされます。スケーリングおよび平均移動されたバージョンの W(ω) を評価することで、フィルター係数 g_k[m] が形成されます。

g_k[m] = W((m ζ_s/L - ζ_k)/Ω_k)

(m = 0, …, L-1 と表現)。ここで、L は信号長です。既定の設定では、cqt は 'hann' ウィンドウを使用します。

不確かさの原理により、帯域幅のサイズは時間シフトの値を制約します。フレームの不等式を満たすには、g_k のシフト a_k が次を満たさなければなりません。

a_k ≤ ζ_k/Ω_k.

前述のように、ウィンドウは周波数領域で適用されます。 ζ_k を中心とするフィルター g_k は形成され、信号のフーリエ変換に適用されます。逆変換を行うと、定 Q 係数が得られます。

参考文献

[1] Jaillet, Florent. “Représentation et traitement temps-fréquence des signaux audionumériques pour des applications de design sonore.” Ph.D. dissertation, Université de la Méditerranée, Aix-Marseille II, 2005.

[2] Balazs, P., M. Dörfler, F. Jaillet, N. Holighaus, and G. Velasco. “Theory, Implementation and Applications of Nonstationary Gabor Frames.” Journal of Computational and Applied Mathematics 236, no. 6 (October 2011): 1481–96. https://doi.org/10.1016/j.cam.2011.09.011.

[3] Holighaus, Nicki, M. Dörfler, G. A. Velasco, and T. Grill. “A Framework for Invertible, Real-Time Constant-Q Transforms.” IEEE Transactions on Audio, Speech, and Language Processing 21, no. 4 (April 2013): 775–85. https://doi.org/10.1109/TASL.2012.2234114.

[4] Velasco, G. A., N. Holighaus, M. Dörfler, and T. Grill. "Constructing an invertible constant-Q transform with nonstationary Gabor frames." In Proceedings of the 14th International Conference on Digital Audio Effects (DAFx-11). Paris, France: 2011.

[5] Schörkhuber, C., A. Klapuri, N. Holighaus, and M. Dörfler. "A MATLAB^® Toolbox for Efficient Perfect Reconstruction Time-Frequency Transforms with Log-Frequency Resolution." Submitted to the AES 53rd International Conference on Semantic Audio. London, UK: 2014.

[6] Průša, Z., P. L. Søndergaard, N. Holighaus, C. Wiesmeyr, and P. Balazs. The Large Time-Frequency Analysis Toolbox 2.0. Sound, Music, and Motion, Lecture Notes in Computer Science 2014, pp 419–442. https://github.com/ltfat

参考

icqt | cqt