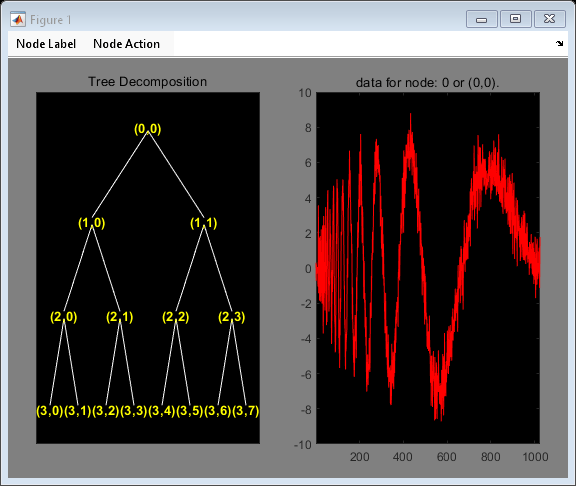
wpdec

1 次元ウェーブレット パケット分解

構文

tobj = wpdec(x,n,wname)

tobj = wpdec(x,n,wname,etype,p)

説明

tobj = wpdec(x,n,wname) は、Shannon エントロピーと wname で指定されたウェーブレットを使用して、レベル n でのベクトル x のウェーブレット パケット分解に対応するウェーブレット パケット ツリー オブジェクト tobj を返します (詳細については、wfilters を参照)。

tobj = wpdec(x,n,wname,etype,p) は、etype で指定されたエントロピー タイプを使用します。p は、etype の値に依存するオプションのパラメーターです。

メモ

tobj = wpdec(x,n,wname) は tobj = wpdec(x,n,wname,"shannon") と等価です。

例

ウェーブレット パケット ツリーの可視化

信号を読み込みます。

load noisdopp

Shannon エントロピーを使用し、db1 ウェーブレット パケットによって信号をレベル 3 で分解します。

wpt = wpdec(noisdopp,3,"db1","shannon");

ウェーブレット パケット ツリーをプロットします。

plot(wpt)

入力引数

x — 入力データ

実数値の数値ベクトル

入力データ。実数値の数値ベクトルとして指定します。

データ型: double

n — 分解レベル

正の整数

分解レベル。正の整数として指定します。

データ型: double

wname — ウェーブレット

文字ベクトル | string スカラー

ウェーブレット パケット分解で使用するウェーブレット。文字ベクトルまたは string スカラーとして指定します。ウェーブレットは、次のいずれかのウェーブレット ファミリから指定します。最適局在化 Daubechies、Beylkin、Coiflet、Daubechies、Fejér-Korovkin、Haar、Han 線形位相モーメント、Morris 最小帯域幅、Symlet、Vaidyanathan、Discrete Meyer、双直交、および逆双直交。各ファミリの利用可能なウェーブレットについては、wfilters を参照してください。

etype — エントロピー タイプ

"shannon" | "log energy" | "threshold" | "sure" | "norm" | "user" | "FunName"

エントロピー タイプ。次のいずれかとして指定します。

エントロピー タイプ (T)	しきい値パラメーター (p)	コメント
"shannon"		p は使用されません。
"log energy"		p は使用されません。
"threshold"	0 ≤ p	p はしきい値です。
"sure"	0 ≤ p	p はしきい値です。
"norm"	1 ≤ p	p はべき乗です。
"user"	string	p には、単一の入力 x をもつ独自のエントロピー関数のファイル名が格納されます。
"FunName"	p の制約なし	FunName は、リストされている前述のエントロピー タイプ以外の任意の string です。 FunName には独自のエントロピー関数のファイル名が格納され、x が入力、p がエントロピー関数の追加パラメーターとして使用されます。

etype としきい値パラメーター p の双方によって、エントロピー基準が定義されます。詳細については、エントロピーを参照してください。

メモ

"user" は過去のオプションです。互換性のために保持されていますが、上記の表で説明されている最後のオプションによって旧式となっています。FunName オプションは、"user" オプションと同様に機能することに加え、独自のエントロピー関数にパラメーターを渡すことができるようになっています。

p — しきい値パラメーター

実数 | string

しきい値パラメーター。実数または string で指定します。p とエントロピー タイプ etype の双方により、エントロピー基準が定義されます。

詳細

ウェーブレット パケット分解

ウェーブレット パケットの手法はウェーブレット分解の一般化であり、より豊かな信号解析を提供します。ウェーブレット パケットの原子は、3 つの自然に解釈されるパラメーター (ウェーブレット分解における位置とスケール、および周波数) でインデックス付けされた波形です。

与えられた直交ウェーブレット関数に対し、ウェーブレット パケットの基底のライブラリが生成されます。これらの基底はそれぞれ、信号を符号化し、グローバル エネルギーを保存し、正確な特徴を再構成する特定の方法を提供します。このウェーブレット パケットを使用して、与えられた信号をさまざまに拡張できます。

ウェーブレット パケット分解と最適な分解の選択の両方にシンプルで効率的なアルゴリズムが存在します。さらに、最適な信号符号化およびデータ圧縮での直接の応用で、適応フィルター処理アルゴリズムを生成できます。

直交ウェーブレット分解の処理において、一般的な手順では Approximation 係数を 2 つの部分に分割します。分割後、Approximation 係数から成るベクトルと Detail 係数から成るベクトルが、ともに粗いスケールで得られます。連続する 2 つの Approximation の間で失われた情報は、Detail 係数に取得されています。次の手順は新しい Approximation 係数ベクトルの分割で構成されます。一連の Detail が再解析されることはありません。

ウェーブレット パケットでは同様の状況で、Approximation ベクトルの分割と同じ方法を使用して、各 Detail 係数ベクトルも 2 つの部分に分解されます。これにより、極めて豊かな解析が提供されます。1 次元の場合には完全二分木が生成され、2 次元の場合には四分木が生成されます。

エントロピー

加法的性質を満たす関数は、二分木構造の効率的な検索とウェーブレット パケット分解の基本的な特性分割に適しています。古典的なエントロピーベースの基準はこれらの条件に適合し、与えられた信号の正確な表現について情報関連の性質を表します。エントロピーは、さまざまな分野に共通の概念であり、主に信号処理で使われます。

以下に、さまざまなエントロピー基準を示します。これ以外にも多くのものが利用でき、簡単に統合できます。式において、s は信号、(s_i)_i は正規直交基底での s の係数です。

エントロピー E は、E(0) = 0 かつ次を満たす加法的コスト関数でなければなりません。

$$E(s)={\displaystyle {\sum }_{i}E(s_i)}.$$

• (非正規化) Shannon エントロピー。

  $$E1(s_i)=-s_i^2\log (s_i^2),$$

  したがって

  $$E1(s)=-{\displaystyle {\sum }_i{s}_i^2\log (s_i^2)},$$

  ただし、0 log(0) = 0 とします。

• l^p ノルム エントロピー (1 ≤ p) での集中度。

  $$E2(s_i)={\left|s_i\right|}^p,$$

  したがって

  $$E2(s)={\displaystyle {\sum }_i{\left|s_i\right|}^p}={\Vert s\Vert }_p^p.$$

• "対数エネルギー" エントロピー。

  $$E3(s_i)=\log (s_i^2),$$

  したがって

  $$E3(s)={\displaystyle {\sum }_i\log (s_i^2)},$$

  ただし、log(0) = 0 とします。

• しきい値エントロピー。

  $$\left|s_i\right|>p$$ では $$E4(s_i)=1$$ であり、それ以外では 0 であるため、E4(s) = # {$$\left|s_i\right|>p$$ となる i} は、信号がしきい値 p より大きい時点の数です。

• "SURE" エントロピー。

  E5(s) = n – #{$$\left|s_i\right|\le p$$ となる i}$$+{\displaystyle {\sum }_i\min }(s_i^2,p^2),$$。ここで、n は信号の長さです。

ヒント

• 1 次元多重信号のウェーブレット パケット変換を取得するには、dwpt を使用します。

アルゴリズム

ウェーブレット パケット分解に使用されるアルゴリズムは、ウェーブレット分解プロセスとほぼ同じです (詳細については、dwt および wavedec を参照)。

参照

[1] Coifman, R.R., and M.V. Wickerhauser. “Entropy-Based Algorithms for Best Basis Selection.” IEEE Transactions on Information Theory 38, no. 2 (March 1992): 713–18. https://doi.org/10.1109/18.119732.

[2] Meyer, Yves. Les ondelettes. Algorithmes et applications, Colin Ed., Paris, 2nd edition, 1994. (English translation: Wavelets: Algorithms and Applications, SIAM).

[3] Wickerhauser, M.V. "INRIA lectures on wavelet packet algorithms." Proceedings ondelettes et paquets d'ondes, 17–21 June 1991, Rocquencourt, France, pp. 31–99.

[4] Wickerhauser, Mladen Victor. Adapted Wavelet Analysis from Theory to Software. Wellesley, MA: A.K. Peters, 1994.

バージョン履歴

R2006a より前に導入

参考

wavedec | waveinfo | wenergy | wprec | dwpt | idwpt

トピック

• Build Wavelet Tree Objects
• Examples Using Wavelet Packet Tree Objects
• Objects in the Wavelet Toolbox Software