wentropy

ウェーブレット エントロピー

構文

ent = wentropy(X)

ent = wentropy(X,Name=Value)

[ent,re] = wentropy(___)

説明

ent = wentropy(X) は、X の正規化された Shannon ウェーブレット エントロピーを返します。

ent = wentropy(X,Name=Value) は、1 つ以上の名前と値の引数を使用してオプションを指定します。

[ent,re] = wentropy(___) は、ウェーブレットの相対エネルギーも返します。

例

ウェーブレット エントロピーの取得

Shannon エントロピー

サンプルが 0 と 2 の交互の値である信号を作成します。

n = 0:499;
x = 1+(-1).^n;
stem(x)
axis tight
title("Signal")
xlim([0 50])

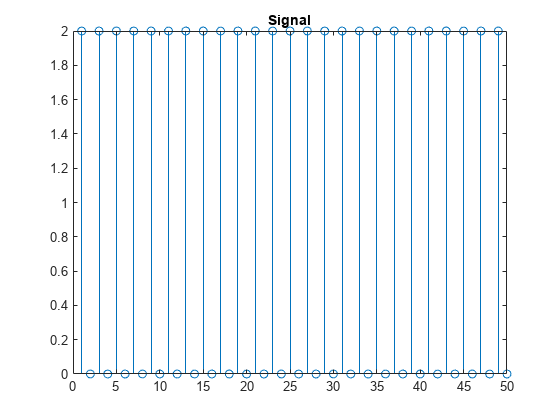
信号のスケーリングされた Shannon エントロピーを取得します。1 レベルのウェーブレット変換を指定し、既定のウェーブレットとウェーブレット変換を使用します。

ent = wentropy(x,Level=1);
ent

ent = 2×1

    1.0000
    1.0000

スケーリングされていない Shannon エントロピーを取得します。エントロピーを log(n) で除算します。ここで、n は信号の長さです。結果とスケーリング エントロピーが等しいことを確認します。

ent2 = wentropy(x,Level=1,Scaled=false);
ent2/log(length(x))

ans = 2×1

    1.0000
    1.0000

最初の信号からゼロ平均信号を作成します。1 レベルのウェーブレット変換を使用して、新しい信号のスケーリングされた Shannon エントロピーを取得します。

x = x-1;
ent = wentropy(x,Level=1);
ent

ent = 2×1

    1.0000
         0

Renyi エントロピー

阪神淡路大震災のデータを読み込みます。データのレベル 4 の調整可能な Q 係数ウェーブレット変換を、2 に等しい品質係数を使用して取得します。

load kobe
wt = tqwt(kobe,Level=4,QualityFactor=2);

調整可能な Q 係数変換の Renyi エントロピー推定を取得します。

ent = wentropy(wt,Entropy="Renyi");
ent

ent = 5×1

    0.8288
    0.8506
    0.8582
    0.8536
    0.7300

ECG データを読み込みます。"db4" ウェーブレットを使用して、信号のレベル 5 離散ウェーブレット変換を取得します。

load wecg
wv = "db4";
[C,L] = wavedec(wecg,5,wv);

ウェーブレットと Approximation 係数を、ウェーブレット エントロピーの計算に適した cell 配列にパッケージ化します。

X = detcoef(C,L,"cells");
X{end+1} = appcoef(C,L,wv);

スケール別に Renyi エントロピーを取得します。

ent = wentropy(X,Entropy="Renyi");
ent

ent = 6×1

    0.2412
    0.5239
    0.5459
    0.6520
    0.7661
    0.8547

Tsallis エントロピー

クロネッカー デルタ シーケンスを作成します。

N = 512;
seq = zeros(1,N);
seq(N/2) = 1;

信号のスケーリングされた Shannon エントロピーを取得します。レベル 3 ウェーブレット変換を指定します。

ShannonEntropy = wentropy(seq,Level=3);

指数のさまざまな値について、信号のスケーリング Tsallis エントロピーを取得します。指数が 1 になると Tsallis エントロピーが Shannon エントロピーに近づくことを確認します。

exps = 3:-1/4:1;
TsallisExponent = zeros(length(exps),1);
TsallisEntropy = zeros(length(exps),4);
ctr = 1;
for k=exps
    ent2 = wentropy(seq,Level=3,Entropy="Tsallis",Exponent=k);
    TsallisExponent(ctr) = k;
    TsallisEntropy(ctr,:) = ent2';
    ctr = ctr+1;
end
TsallisTable = table(TsallisExponent,TsallisEntropy)

TsallisTable=9×2 table
    TsallisExponent                 TsallisEntropy             
    _______________    ________________________________________

            3          0.71454    0.87888    0.97069    0.98285
         2.75          0.67651    0.84955    0.95685    0.97233
          2.5          0.63178    0.81187    0.93596     0.9552
         2.25          0.57852     0.7628    0.90407    0.92718
            2          0.51437    0.69812    0.85499    0.88149
         1.75          0.43679    0.61258    0.77985    0.80825
          1.5          0.34491    0.50213    0.66897    0.69658
         1.25          0.24402    0.37071    0.52076    0.54417
            1           0.1495    0.23839      0.356    0.37278

ShannonEntropy'

ans = 1×4

    0.1495    0.2384    0.3560    0.3728

入力引数

X — 入力データ

実数値のベクトル | 実数値の行列 | cell 配列

入力データ。実数値の行ベクトルまたは列ベクトル、実数値の行ベクトルまたは列ベクトルの cell 配列、または 2 行以上の実数値の行列として指定します。

• X が行ベクトルまたは列ベクトルの場合、X は少なくとも 4 つのサンプルをもたなければならず、関数は X が時間データを表すと仮定します。

• X が cell 配列の場合、関数は X が実数値の行ベクトルまたは列ベクトルの間引きウェーブレット変換または間引きウェーブレット パケット変換であると仮定します。

• X が 2 行以上の行列である場合、関数は X が実数値の行ベクトルまたは列ベクトルの最大重複離散ウェーブレット変換または最大重複離散ウェーブレット パケット変換であると仮定します。

例: ent = wentropy(randn(1,1024)) は、正規化された Shannon ウェーブレット エントロピーを返します。wentropy は、modwt の既定のオプションを使用してウェーブレット係数を計算します。

データ型: single | double

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

例: ent = wentropy(X,Wavelet="coif4") は "coif4" ウェーブレットを使用してウェーブレット変換を取得します。

Entropy — エントロピー

"Shannon" (既定値) | "Renyi" | "Tsallis"

wentropy によって返されるエントロピー。"Shannon"、"Renyi"、および "Tsallis" のいずれかとして指定します。詳細については、ウェーブレット エントロピーを参照してください。

Exponent — 指数

2 (既定値) | 実数スカラー

Renyi エントロピーおよび Tsallis エントロピーで使用する指数。実数スカラーとして指定します。

• Renyi エントロピーの場合、指数は非負でなければなりません。

• Tsallis エントロピーの場合、指数は –1/2 以上でなければなりません。

• Renyi エントロピーと Tsallis エントロピーの場合、Exponent=1 を指定することは限定的なケースであり、Shannon エントロピーが生成されます。

Exponent の指定は、Entropy が "Renyi" または "Tsallis" の場合のみ有効です。詳細については、ウェーブレット エントロピーを参照してください。

メモ

Tsallis エントロピーに対して負の指数を指定すると、ウェーブレット係数エネルギーの小さな変化でもエントロピー値が大幅に変化し、エントロピーの計算結果が不安定になる可能性があります。

データ型: single | double

Transform — 変換

"modwt" (既定値) | "dwt" | "dwpt" | "modwpt"

ウェーブレットまたはウェーブレット パケット係数を取得するために使用する変換。次のいずれかとして指定します。

• "dwt" — 離散ウェーブレット変換

• "dwpt" — 離散ウェーブレット パケット変換

• "modwt" — 最大重複離散ウェーブレット変換

• "modwpt" — 最大重複離散ウェーブレット パケット変換

すべての変換に周期的拡張が使用されます。

入力データがウェーブレットまたはウェーブレット パケット係数の場合、変換の指定は無効です。

Level — ウェーブレット分解レベル

正の整数

入力 X が時間データの場合のウェーブレット分解レベル。正の整数として指定します。関数 wentropy は、指定されたレベルまでのウェーブレット変換を取得します。指定しない場合、既定のレベルは変換のタイプと信号長 N によって異なります。

• Transform が "dwt" または "modwt" の場合、Level は既定で floor(log2(N))-1 になります。

• Transform が "dwpt" または "modwpt" の場合、Level は既定で min(4,floor(log2(N))-1) になります。

入力データがウェーブレットまたはウェーブレット パケット係数の場合、レベルの指定は無効です。

データ型: single | double

Wavelet — ウェーブレット

文字ベクトル | string スカラー

変換で使用するウェーブレット。文字ベクトルまたは string スカラーとして指定します。Transform が "modwt" または "modwpt" の場合、ウェーブレットは直交でなければなりません。既定のウェーブレットは、Transform の値によって異なります。

• Transform が "dwt" または "modwt" の場合、wentropy は "sym4" ウェーブレットを使用します。

• Transform が "dwpt" または "modwpt" の場合、wentropy は "fk18" ウェーブレットを使用します。

サポートされている直交ウェーブレットと双直交ウェーブレットのリストについては、wfilters を参照してください。

入力データがウェーブレットまたはウェーブレット パケット係数である場合、ウェーブレット名の指定は無効です。

データ型: char | string

Distribution — 正規化方式

"scale" (既定値) | "global"

ウェーブレット変換係数の経験的確率分布を取得するために使用する正規化方式。"scale" または "global" として指定します。

• "global" — 関数は、すべての係数の振幅の 2 乗の総和によって、係数の振幅の 2 乗を正規化します。ウェーブレット変換の各スケールはスカラーを生成し、これらの値のベクトルが確率ベクトルを形成します。関数はこのベクトルでエントロピー計算を実行し、全体のエントロピーはスカラーになります。

• "scale" — 関数は、各スケールで個別にウェーブレット係数を正規化し、スケール別にエントロピーを計算します。

  • 入力が時系列データの場合、出力 ent のサイズは (Ns+1) 行 1 列になります。ここで、Ns はスケールの数です。

  • 入力が cell 配列または行列の場合、ent のサイズは M 行 1 列になります。ここで、M は cell 配列の長さ、または行列の行数です。

詳細については、ウェーブレット エントロピーを参照してください。

Scaled — ウェーブレット エントロピーのスケーリング

true または 1 (既定値) | false または 0

ウェーブレット エントロピーのスケーリングの logical 値。数値または logical の 1 (true) または 0 (false) として指定します。true として指定した場合、関数 wentropy は、指定されたエントロピーの一様分布に対応する係数でウェーブレット エントロピーをスケーリングします。

• Shannon エントロピーと Renyi エントロピーの場合、係数は 1/log(Nj) です。Nj は、Distribution が "scale" の場合はスケール別のサンプルのデータの長さ、Distribution が "global" の場合はスケールの数です。

• Tsallis エントロピーの場合、係数は (Exponent-1)/(1-Nj^(1-Exponent)) です。

Scaled=false に設定すると、ウェーブレット エントロピーはスケーリングされません。

データ型: logical

EnergyThreshold — エネルギーしきい値

1e-8 (既定値) | 非負のスカラー

エネルギーしきい値。非負のスカラーとして指定します。関数は、スケール別のエネルギーが EnergyThreshold 未満の係数をすべて 0 に置き換えます。正の EnergyThreshold は、関数が、エネルギーの大きくないウェーブレットまたはウェーブレット パケット係数を高エントロピーのシーケンスとして扱うことを防ぎます。

データ型: single | double

出力引数

ent — エントロピー

スカラー | ベクトル

X のエントロピー。スカラーまたはベクトルとして返されます。

• X が時間データの場合、ent はスケール別のエントロピー推定の実数値 (Ns+1) 行 1 列のベクトルになります。ここで、Ns はスケールの数です。

• X がウェーブレットまたはウェーブレット パケット変換入力の場合、ent は、X の長さに等しい長さをもつ実数値の列ベクトル (X が cell 配列の場合) または X の行の次元 (X が行列の場合) になります。

ウェーブレット エントロピーのグローバルな推定値を取得するには、Distribution を参照してください。関数 wentropy は、自然対数を使用してエントロピーを計算します。

データ型: single | double

re — 相対ウェーブレット エネルギー

ベクトル | 行列

相対ウェーブレット エネルギー。ベクトルまたは行列として返されます。

• Distribution="scale" の場合、関数は係数およびスケールごとの相対ウェーブレット エネルギーを返します。

• Distribution="global" の場合、関数はスケールごとの相対ウェーブレット エネルギーを返します。

係数エネルギーが EnergyThreshold の値未満のスケールは 0 に等しくなります。

データ型: single | double

詳細

ウェーブレット エントロピー

ウェーブレット エントロピー (WE) は、非定常信号の解析によく使用されます。WE は、ウェーブレットまたはウェーブレット分解を、スケール別のウェーブレット係数内における次数の尺度と組み合わせます。これらの次数の尺度は "エントロピー尺度" と呼ばれます。WE は正規化されたウェーブレット係数を経験的確率分布として扱い、そのエントロピーを計算します。

2 つの方法のいずれかで、ウェーブレット係数 $$\left\{w{t}_{ij}\right\}$$ を正規化できます。

• 関数は次のように、係数の 2 乗の総和によってすべての係数を正規化します。$$E={\displaystyle \sum _i{\displaystyle \sum _j|}}w{t}_{ij}{|}^2,$$ ここで、j は時間に対応し、i はスケールに対応します。確率質量関数は次のようになります。$$\mathbb{P}(w{t}_i)={\displaystyle \sum _j\frac{|w{t}_{ij}{|}^2}{E}}.$$ この正規化を使用するには、Distribution を "global" に設定します。

• 関数は、各スケールでの係数を、それらの振幅の 2 乗の合計によって個別に正規化します。$$E_i={\displaystyle \sum _j|}w{t}_{ij}{|}^2.$$ 確率質量関数は次のようになります。$$\mathbb{P}\left(w{t}_{ij}\right)=|w{t}_{ij}{|}^2/E_i.$$ この正規化を使用するには、Distribution を "scale" に設定します。

関数 wentropy は、3 つのエントロピー測定をサポートします。

• Shannon エントロピー

  離散確率変数 X の場合、Shannon エントロピーは次のように定義されます。

  $$H(X)=-{\displaystyle \sum _i\mathbb{P}}(X=x_i)\ln (\mathbb{P}(X=x_i)),$$

  ここで、確率変数が取り得るすべての値にわたって合計が取られます。慣例により、0 ln(0) = 0 になります。

• Renyi エントロピー

  Renyi エントロピーは次のように定義されます。

  $$H_r(X)=\frac{1}{1-\alpha }\text{ln}\left({\displaystyle \sum _i{\left(\mathbb{P}(X=x_i)\right)}^{\alpha }}\right),\alpha \ge \text{ 0}\text{.}$$

  極限における Renyi エントロピーは Shannon エントロピーになります。$$\underset{\alpha \to 1}{\lim }{H}_r(X)=H(X).$$

• Tsallis エントロピー

  Tsallis エントロピーは次のように定義されます。

  $$H_t(X)=\frac{1}{q-1}\left(1-{\displaystyle \sum _i{\left(\mathbb{P}(X=x_i)\right)}^q}\right),q\in ℝ,q\ne 1.$$

  Renyi エントロピーと同様に、極限における Tsallis エントロピーは Shannon エントロピーになります。$$\underset{q\to 1}{\lim }{H}_t(X)=H(X).$$

参照

[1] Zunino, L., D.G. Pérez, M. Garavaglia, and O.A. Rosso. “Wavelet Entropy of Stochastic Processes.” Physica A: Statistical Mechanics and Its Applications 379, no. 2 (June 2007): 503–12. https://doi.org/10.1016/j.physa.2006.12.057.

[2] Rosso, Osvaldo A., Susana Blanco, Juliana Yordanova, Vasil Kolev, Alejandra Figliola, Martin Schürmann, and Erol Başar. “Wavelet Entropy: A New Tool for Analysis of Short Duration Brain Electrical Signals.” Journal of Neuroscience Methods 105, no. 1 (January 2001): 65–75. https://doi.org/10.1016/S0165-0270(00)00356-3.

[3] Alcaraz, Raúl, ed. "Wavelet Entropy: Computation and Applications." Special issue, Entropy 17 (2015). https://www.mdpi.com/journal/entropy/special_issues/wavelet-entropy.

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意および制限:

• 名前と値の引数 Wavelet、Transform、および Distribution の値は、コンパイル時に定数でなければなりません。coder.Constant (MATLAB Coder) を使用してください。

• ベクトル入力は、コンパイル時に 1 つの次元が 1 に固定されていなければなりません。たとえば、無制限のサイズの行ベクトル入力を許可するには、コンパイル時に 1 番目の入力引数を {coder.typeof(0,[1 Inf],[0 1]])} として指定します。詳細については、coder.typeof (MATLAB Coder) を参照してください。

• 行入力と列入力の両方に可変サイズの次元を使用してコンパイルすると、生成されたコードは行列入力を想定します。たとえば、コンパイル時に 1 番目の入力引数を {coder.typeof(0,[1 Inf],[1 1])} として指定すると、生成コードは行ベクトル入力に対してエラーとなります。

• 旧バージョンの関数 wentropy で使用されていた構文はサポートされません。詳細については、バージョン履歴を参照してください。

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

wentropy 関数は GPU 配列入力をサポートしますが、次の使用上の注意および制限があります。

• "dwpt" 変換はサポートされません。

• 旧バージョンの関数 wentropy で使用されていた構文はサポートされません。詳細については、バージョン履歴を参照してください。

詳細については、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2006a より前に導入

R2023a: wentropy は C/C++ コード生成と gpuArray オブジェクトをサポートする

関数 wentropy は以下をサポートします。

• C/C++ コード生成。C/C++ コードを生成するには、MATLAB^® Coder™ が必要です。

• gpuArray オブジェクト入力。gpuArray オブジェクトを使用するには、Parallel Computing Toolbox™ が必要です。

R2022b: wentropy の入力構文は変更済み

旧バージョンの wentropy で使用されていた構文は引き続き機能しますが、推奨されなくなりました。旧バージョンでは、エントロピーの推定方法に対する制御が最小限でした。関数 wentropy は、入力構文から、どのバージョンを使用するかを自動的に決定します。

両方のバージョンの wentropy で Shannon エントロピーを指定できます。ただし、旧バージョンでは入力データに関する仮定がないため、新バージョンと同じ結果を再現するために多大な労力が必要になる場合があります。

旧バージョン	新バージョン
load wecg n = numel(wecg); lev = 3; wt = modwt(wecg,lev); energy = sum(abs(wt).^2,2); wt2 = abs(wt)./sqrt(energy); ent = zeros(lev+1,1); for k=1:lev+1 ent(k) = wentropy(wt2(k,:),'shannon')/log(n); end ent ent = 0.3925 0.6512 0.6985 0.9329	load wecg ent = wentropy(wecg,Level=3) ent = 0.3925 0.6512 0.6985 0.9329

参考

wavedec | dwpt | modwt | modwpt