ウェーブレットとは

ウェーブレットとは、ゼロおよび非ゼロ ノルムの平均値を持つ、持続時間が事実上限定されている波形のことです。

対象となる多くの信号およびイメージが、過渡状態によって中断された区分的な平滑化動作を示します。音声信号は、子音を符号化している短いバーストと、それに続く母音を示す定常状態の振動によって特徴付けられます。自然イメージにはエッジがあります。金融時系列は、経済状況における急速な好転と悪化を特徴付ける過渡動作を示します。フーリエの原理とは異なり、ウェーブレットの原理は、過渡動作を含む区分的な規則正しい信号とイメージをまばらに表現することを得意としています。

ウェーブレットと、フーリエ解析の基盤である正弦波を比較します。正弦波の持続時間は制限されず、マイナスからプラスの無限大に伸びています。正弦波は滑らかで予測可能ですが、ウェーブレットは不規則で非対称である傾向があります。

フーリエ解析は、信号をさまざまな周波数の正弦波に分割して構成されています。同じように、ウェーブレット解析は、元の (または "マザー") ウェーブレットをシフトおよびスケーリングしたバージョンに信号を分割することです。

ウェーブレットおよび正弦波の図を見るだけで、鋭い変化のある信号は滑らかな正弦波よりも不規則なウェーブレットを使用した方が適切に解析できることが直感的にわかります。

また、局所特徴は、局所範囲を持つウェーブレットを使用した方が適切に説明できることもわかります。次の例では、不連続点がある正弦波で構成されたシンプルな信号について、このことを説明します。

正弦波における不連続点の位置決定

この例は、ウェーブレット解析によって正弦波の不連続点の位置を特定できることを示しています。

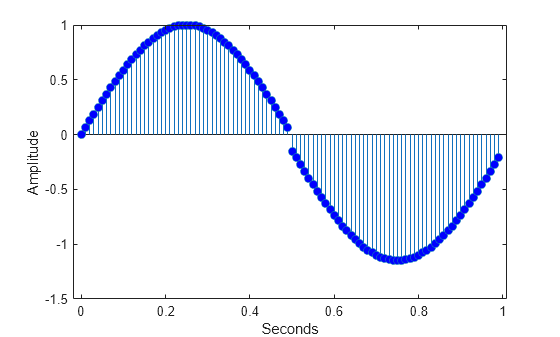
100 Hz でサンプリングした 1 Hz の正弦波を作成します。正弦波の持続時間は 1 秒です。この正弦波では $$t=0.5$$ 秒の時点に不連続点があります。

t = linspace(0,1,100)';
x = sin(2*pi*t);
x1 = x-0.15;
y = zeros(size(x));
y(1:length(y)/2) = x(1:length(y)/2);
y(length(y)/2+1:end) = x1(length(y)/2+1:end);
stem(t,y,'markerfacecolor',[0 0 1]); 
xlabel('Seconds'); 
ylabel('Amplitude');

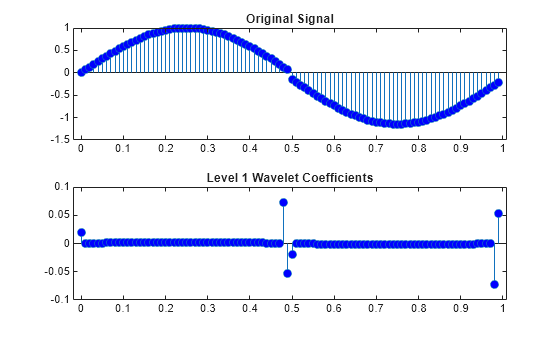
'sym2' ウェーブレットを使用して正弦波の非間引き離散ウェーブレット変換を求め、ウェーブレット (Detail) 係数と元の信号をプロットします。

[swa,swd] = swt(y,1,'sym2');
subplot(211)
stem(t,y,'markerfacecolor',[0 0 1]); 
title('Original Signal');
subplot(212)
stem(t,swd,'markerfacecolor',[0 0 1]);
title('Level 1 Wavelet Coefficients');

1 Hz の正弦波に関するフーリエ係数の振幅を不連続点がある場合とない場合で比較します。

dftsig = fft([x y]);
dftsig = dftsig(1:length(y)/2+1,:);
df = 100/length(y);
freq = 0:df:50;
stem(freq,abs(dftsig));
xlabel('Hz'); ylabel('Magnitude');
legend('sine wave','sine wave with discontinuity');

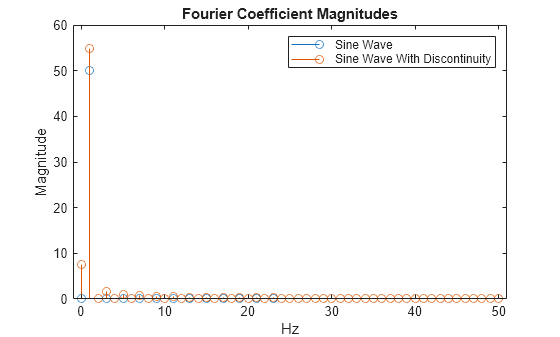
フーリエ係数の振幅の差異は最小です。離散フーリエ基底ベクトルは時間間隔全体をサポートするため、離散フーリエ変換での不連続点の検出はウェーブレット変換ほど効率的ではありません。

正弦波のレベル 1 ウェーブレット係数を不連続点がある場合とない場合で比較します。

[swax,swdx] = swt(x,1,'sym2');
subplot(211)
stem(t,swd); title('Sine Wave with Discontinuity (Wavelet Coefficients)');
subplot(212)
stem(t,swdx); title('Sine Wave (Wavelet Coefficients)');

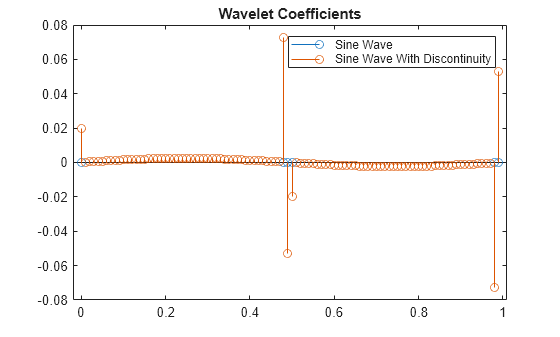
2 つの信号のウェーブレット係数は有意差を示しています。多くの場合、ウェーブレット解析では、他の解析手法が見落としてしまう信号またはイメージの特性 (トレンド、降伏点、高次導関数における不連続点、自己相似性など) を明らかにすることができます。さらに、ウェーブレットはフーリエ手法によって提示されるビューとは異なるデータ ビューを提供するため、ウェーブレット解析では信号を感知できるほど劣化することなく大幅に圧縮またはノイズ除去できることがしばしばあります。

×

例を開く

この例の変更されたバージョンがあります。編集された方の例を開きますか?

いいえ、変更されたバージョンを上書きします。 はい