大きくサンプリングされているウェーブレットの再構成

離散ウェーブレット変換を使用して信号およびイメージを解析、または分解する方法を学習しました。このプロセスは、"分解" または "解析" と呼ばれます。話の残り半分は、これらの成分を、情報の欠落なしに元の信号に組み立て戻す方法についてです。このプロセスは、"再構成" または "合成" と呼ばれます。合成をもたらす数学的操作は "逆離散ウェーブレット変換" (IDWT) と呼ばれます。

Wavelet Toolbox™ ソフトウェアを使用して信号を合成するには、信号をウェーブレット係数から再構成します。

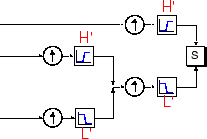
ウェーブレット解析にはフィルター処理とダウンサンプリングが含まれているように、ウェーブレットの再構成プロセスはアップサンプリングとフィルター処理で構成されています。アップサンプリングは、サンプル間に 0 を挿入することで信号成分を長くするプロセスです。

ツールボックスには idwt および waverec などのコマンドが含まれており、1 次元信号の成分について、それぞれ単一レベルまたは多重レベルの再構成を行います。これらのコマンドには、2 次元および 3 次元用の idwt2、waverec2、idwt3、および waverec3 という類似のものがあります。

再構成フィルター

再構成プロセスのフィルター処理の部分についても議論の余地があります。フィルターの選択が、元の信号の完全再構成を達成する上で特に重要なためです。

分解フェーズ中に実行される信号成分のダウンサンプリングは、エイリアシングと呼ばれる歪みを導入します。分解フェーズと再構成フェーズとで密接な関連をもつ (ただし同一ではない) フィルターを注意深く選択することで、エイリアシングの影響を "相殺" できることがわかります。

これらのフィルターの設計方法についての技術的な議論は、Strang および Nguyen による『Wavelets and Filter Banks』という本の 347 ページにあります。ローパスおよびハイパス分解フィルター (L および H) は、それぞれ関連する再構成フィルター (L' および H') と共に、"直交ミラーフィルター" と呼ばれるシステムを形成します。

Approximation および Detail の再構成

元の信号を Approximation 係数および Detail 係数から再構成できることを見てきました。

Approximation および Detail 自体を、その係数ベクトルから再構成することもできます。例として、第 1 レベルの Approximation A1 を係数ベクトル cA1 から再構成する方法を考えます。

係数ベクトル cA1 を、元の信号を再構成するのに使用したのと同じプロセスに通します。ただし、それを第 1 レベルの Detail cD1 と結合するのではなく、Detail 係数ベクトルの代わりに 0 のベクトルを与えます。

このプロセスで、再構成された Approximation A1 が得られます。これは元の信号 S と同じ長さであり、実際のその Approximation です。

同様に、類似のプロセスを使用して、第 1 レベルの Detail D1 を再構成できます。

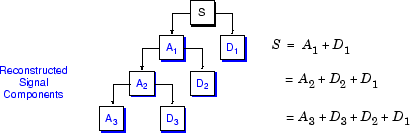
再構成された Detail および Approximation は、元の信号の真の構成要素です。実際、それらを組み合わせると、次のことがわかります。

A₁ + D₁ = S.

係数ベクトル cA1 および cD1 は — ダウンサプリングによって生成され、元の信号の半分長さしかないため — 信号を再現するために直接結合できないことに注意してください。Approximation および Detail を結合する前に再構成する必要があります。

この手法を多重レベルの解析の成分に拡張すると、類似の関係がすべての再構成された信号の構成要素についてみられることがわかります。つまり、元の信号を再作成する方法はいくつかあります。

共役ミラーフィルターからのウェーブレット

再構成フィルター節で、適切なフィルターの選択の重要性について説明しました。実際、フィルターの選択は、完全再構成が可能かどうかを決定するだけでなく、解析を実行するのに使用するウェーブレットの形状も決定します。

実用的なユーティリティを備えたウェーブレットを作成する場合、波形の描画から始めることはまずありません。そうではなく、適切な直交ミラーフィルターを設計し、それらを使用して波形を作成する方が、通常は理にかなっています。この方法を、例に注目して見ていきましょう。

db2 ウェーブレットのローパス再構成フィルター (L') について考えます。

フィルター係数は、関数 dbaux から求めることができます。スケーリングフィルターベクトルの順序を逆にし、すべての偶数要素 (1 からインデックス付け) を (-1) と掛け合わせると、ハイパスフィルターが得られます。

2 でのアップサンプリングと、その出力のスケーリングフィルターでの畳み込みを繰り返すことで、Daubechies の極値位相ウェーブレットが生成されます。

 L = dbaux(2);
 H = wrev(L).*[1 -1 1 -1];
 HU = dyadup(H,0);
 HU = conv(HU,L);
 plot(HU); title('1st Iteration');
 H1 = conv(dyadup(HU,0),L);
 H2 = conv(dyadup(H1,0),L);
 H3 = conv(dyadup(H2,0),L);
 H4 = conv(dyadup(H3,0),L);
 figure;
 for k =1:4
 subplot(2,2,k);
 eval(['plot(H' num2str(k) ')']);
 axis tight;
 end

曲線が徐々に db2 ウェーブレットに似てきます。これは、ウェーブレットの形状が完全に再構成フィルターの係数によって決定されることを意味します。

この関係には深い意味があります。形状だけを選択して、それをウェーブレットと呼んだり、解析を実行することはできないことを意味しています。少なくとも、元の信号を正確に再構成可能にする必要がある場合には、任意のウェーブレット波形を選ぶことはできません。直交ミラー再構成フィルターによって決定される形状を選択するしかありません。

スケーリング関数

ウェーブレットと直交ミラーフィルターの相互関係をみてきました。ウェーブレット関数 ψ は、ハイパスフィルターによって決定されます。このフィルターはウェーブレット分解の Detail も生成します。

すべてではありませんが一部のウェーブレットに関連する他の関数があります。これがいわゆるスケーリング関数 ϕ です。スケーリング関数はウェーブレット関数と非常に似ています。ローパス直交ミラーフィルターによって決定され、そのためウェーブレットの分解の Approximation に関連付けられます。

同様に、ハイパスフィルターのアップサンプリングと畳み込みを繰り返すとウェーブレット関数を近似する形状が生成され、ローパスフィルターのアップサンプリングと畳み込みを繰り返すとスケーリング関数を近似する形状が生成されます。