シンボリック オブジェクトを使用した数学的オブジェクトの表現

Symbolic Math Toolbox™ で数学の問題を解くには、さまざまな数学的オブジェクトを表現するためのシンボリック オブジェクトを定義します。この例では、以下のシンボリック オブジェクトをコマンド ウィンドウで使用する方法について説明します。

• シンボリック数

• シンボリック スカラー変数、シンボリック関数、およびシンボリック式

• シンボリック方程式

• シンボリック ベクトルとシンボリック行列

• シンボリック行列変数

• シンボリック行列関数

シンボリック数

数値をシンボリック数として定義し、数値近似を使用するのではなく厳密な形式としてその数値を扱うよう MATLAB^® に指定します。たとえば、シンボリック数を使用して逆三角関数 $$\theta ={\sin }^{-1}(1/\sqrt{2})$$ の引数を表現します。

sym を使用してシンボリック数 $$\text{1/}\sqrt{2}$$ を作成し、それを a に代入します。

a = sym(1/sqrt(2))

a =
2^(1/2)/2

a の逆正弦を求めます。結果はシンボリック数 pi/4 です。

thetaSym = asin(a)

thetaSym =
pi/4

シンボリック数を可変精度の演算に変換するには、vpa を使用できます。結果は有効桁数が 32 桁の小数になります。

thetaVpa = vpa(thetaSym)

thetaVpa =
0.78539816339744830961566084581988

シンボリック数を倍精度の数値に変換するには、double を使用します。数値演算とシンボリック演算の選択の詳細については、数値演算またはシンボリック演算の選択を参照してください。

thetaDouble = double(thetaSym)

thetaDouble =
0.7854

シンボリック スカラー変数、シンボリック関数、およびシンボリック式

変数、関数、式をシンボリック オブジェクトとして定義すると、これらのシンボリック オブジェクトを使用して、数式の単純化や方程式の求解などの代数演算を実行できます。たとえば、シンボリック スカラー変数、シンボリック関数、およびシンボリック式を使用して二次関数 $$f(x)=x^2+x-2$$ を表現します。シンボリック スカラー変数は、簡潔に "シンボリック変数" とも呼ばれます。

syms を使用してシンボリック スカラー変数 x を作成します。sym を使用してシンボリック スカラー変数を作成することもできます。syms と sym の選択の詳細については、関数 syms または sym の選択を参照してください。

"シンボリック式" x^2 + x - 2 を定義して 2 次方程式の右辺を表現し、それを f(x) に代入します。ここで、識別子 f(x) は、この二次関数を表現する "シンボリック関数" を参照します。シンボリック関数は、入力引数としてスカラーを受け入れます。

syms x
f(x) = x^2 + x - 2

f(x) =
x^2 + x -2

その後、かっこ内の入力引数を指定して、この二次関数を評価できます。たとえば、f(2) を評価します。

fVal = f(2)

fVal =
4

2 次方程式 $$f(x)=0$$ を解くこともできます。solve を使用して 2 次方程式の根を求めます。solve は 2 つの解を 2 つのシンボリック数のベクトルとして返します。

sols = solve(f)

sols =
-2
 1

シンボリック方程式

数式をシンボリック方程式として定義することで、その方程式の解を求めることができます。たとえば、シンボリック方程式を使用して三角関数の問題 $$2\sin (t)\cos (t)=1$$ を解きます。

syms を使用してシンボリック関数 g(t) を作成します。g(t) にシンボリック式 2*sin(t)*cos(t) を代入します。

syms g(t)
g(t) = 2*sin(t)*cos(t)

g(t) = 
2*cos(t)*sin(t)

方程式を定義するには、== 演算子を使用し、数学的関係 g(t) == 1 を eqn に代入します。識別子 eqn が、この三角関数の問題を表現するシンボリック方程式です。

eqn = g(t) == 1

eqn = 
2*cos(t)*sin(t) == 1

solve を使用して三角関数の問題の解を求めます。

sol = solve(eqn)

sol = 
pi/4

シンボリック ベクトルとシンボリック行列

シンボリック ベクトルとシンボリック行列を使用して線形方程式系を表現し、求解します。

$$\begin{array}{c}x+2y=u\\ 4x+5y=v\end{array}$$

方程式系は、2 つのシンボリック方程式のベクトルとして表現できます。また、方程式系を、シンボリック数の行列とシンボリック変数のベクトルを含む行列問題として表現することもできます。簡潔にするために、シンボリック オブジェクトのベクトルは "シンボリック ベクトル"、シンボリック オブジェクトの行列は "シンボリック行列" と呼びます。

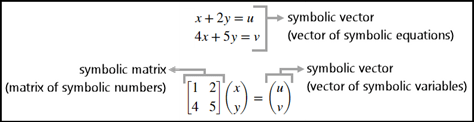
2 つのシンボリック方程式 eq1 と eq2 を作成します。2 つの方程式を組み合わせてシンボリック ベクトルにします。

syms u v x y
eq1 = x + 2*y == u;
eq2 = 4*x + 5*y == v;
eqns = [eq1, eq2]

eqns =
[x + 2*y == u, 4*x + 5*y == v]

solve を使用して eqns で表現される方程式系の解を求めます。solve は、方程式の各変数に基づいて名前が付けられたフィールドをもつ構造体 S を返します。解には、S.x および S.y というドット表記を使用してアクセスできます。

S = solve(eqns);
S.x

ans =
(2*v)/3 - (5*u)/3

S.y

ans =
(4*u)/3 - v/3

線形方程式系を解くための別の方法は、それを行列形式に変換することです。equationsToMatrix を使用して方程式系を行列形式に変換し、出力を A と b に代入します。ここで、A はシンボリック行列であり、b はシンボリック ベクトルです。行列除算演算子 \ を使用して、行列の問題を解きます。

[A,b] = equationsToMatrix(eqns,x,y)

A =
[1, 2]
[4, 5]
 
 
b =
u
v

sols = A\b

sols =
(2*v)/3 - (5*u)/3
    (4*u)/3 - v/3

シンボリック行列変数

R2021a 以降

シンボリック行列変数を使用し、ベクトルについて微分を評価します。

$$\begin{array}{l}\alpha =y^{\text{T}}Ax\\ \frac{\partial \alpha }{\partial x}=y^{\text{T}}A\\ \frac{\partial \alpha }{\partial y}=x^{\text{T}}{A}^{\text{T}}\end{array}$$

シンボリック行列変数は、行列、ベクトル、およびスカラーをコンパクトな行列表記で表現します。シンボリック行列変数は、整形された簡潔な表示で数式をより明確に示します。Symbolic Math Toolbox では、ベクトルベースおよび行列ベースの式をシンボリック行列変数として入力できます。

matrix 構文で syms コマンドを使用して、3 つのシンボリック行列変数 x、y、および A を作成します。非スカラーのシンボリック行列変数は、コマンド ウィンドウおよびライブ エディターにおいて太字で表示されます。

syms x [4 1] matrix
syms y [3 1] matrix
syms A [3 4] matrix
x
y
A

x =
x

y =
y

A =
A

alpha を定義します。シンボリック行列変数 x および y で表現されるベクトル x および y について、alpha の微分を求めます。

alpha = y.'*A*x

alpha =
y.'*A*x

Dx = diff(alpha,x)

Dx =
y.'*A

Dy = diff(alpha,y)

Dy =
x.'*A.'

subs を使用して、Dx の y に [1; 2; 3] を代入し、Dy の x に [-1; 2; 0; 1] を代入します。シンボリック式を評価するときは、定義されたシンボリック行列変数と同じサイズの値を代入しなければなりません。

Dx = subs(Dx,y,[1; 2; 3])

Dx =
symmatrix([1;2;3]).'*A

Dy = subs(Dy,x,[-1; 2; 0; 1])

Dx =
symmatrix([-1;2;0;1]).'*A.'

シンボリック行列関数

R2022a 以降

シンボリック行列関数を使用して、行列多項式を評価します。

$$f(A)=A^2-3A+I_2$$

シンボリック行列関数は、入力引数として行列、ベクトル、およびスカラーを受け入れるパラメーター依存関数を表現します。シンボリック行列関数では、コンパクトな行列表記法で行列の演算を行い、整形された簡潔な表示で数式をより明確に表示します。Symbolic Math Toolbox では、ベクトルベースおよび行列ベースの式をシンボリック行列関数として入力できます。

matrix 構文で syms コマンドを使用して、2 行 2 列のシンボリック行列変数 A を作成します。A の以前の定義を保持するために matrix keepargs 構文で syms コマンドを使用し、入力引数として A を受け入れるシンボリック行列関数 f(A) を作成します。

syms A 2 matrix
syms f(A) 2 matrix keepargs

多項式をシンボリック行列関数に割り当てます。

f(A) = A^2 - 3*A + 2*eye(2)

f(A) =
 
2*symmatrix(eye(2)) - 3*A + A^2

関数を行列値 A = [1 2; -2 -1] について評価します。シンボリック行列関数を評価するときは、定義された入力引数と同じサイズの値を代入しなければなりません。

fEval = f([1 2; -2 -1])

fEval =
 
- 3*symmatrix([1,2;-2,-1]) + symmatrix([1,2;-2,-1])^2 + 2*symmatrix(eye(2))

評価済みの関数を symmatrix データ型から sym データ型に変換します。

fSym = symmatrix2sym(fEval)

fSym =
[-4, -6]
[ 6,  2]

シンボリック オブジェクトの比較

この表は、Symbolic Math Toolbox で使用できるシンボリック オブジェクトの比較です。

シンボリック オブジェクト	MATLAB コマンドの例	シンボリック オブジェクトのサイズ	データ型
シンボリック数	a = 1/sqrt(sym(2)) theta = asin(a) a = 2^(1/2)/2 theta = pi/4	1 行 1 列	sym
シンボリック スカラー変数	syms x y u v	1 行 1 列	sym
シンボリック関数	syms x f(x) = x^2 + x - 2 syms g(t) [1 3] g f(x) = x^2 + x - 2 g(t) = [g1(t), g2(t), g3(t)]	size(g) などの未評価関数のサイズは 1 行 1 列。 size(g(t)) などの評価済み関数のサイズは m 行 n 列。ここで、m は行のサイズ、n は列のサイズ。	class(g) などの未評価関数のデータ型は symfun。 class(g(t)) などの評価済み関数のデータ型は sym。
シンボリック式	syms x expr = x^2 + x - 2 expr2 = 2*sin(x)*cos(x) expr = x^2 + x - 2 expr2 = 2*cos(x)*sin(x)	1 行 1 列	sym
シンボリック方程式	syms u v x y eq1 = x + 2*y == u eq2 = 4*x + 5*y == v eq1 = x + 2*y == u eq2 = 4*x + 5*y == v	1 行 1 列	sym
シンボリック ベクトル	syms u v b = [u v] b = [u, v]	1 行 n 列または m 行 1 列。ここで、m は行のサイズ、n は列のサイズ。	sym
シンボリック行列	syms A x y A = [x y; x*y y^2] A = [ x, y] [x*y, y^2]	m 行 n 列。ここで、m は行のサイズ、n は列のサイズ。	sym
シンボリック多次元配列	syms A [2 1 2] A A(:,:,1) = A1_1 A2_1 A(:,:,2) = A1_2 A2_2	sz1×sz2×...×szn。ここで、szn は n 番目の次元のサイズ。	sym
シンボリック行列変数 ("R2021a 以降")	syms A B [2 3] matrix A B A = A B = B	m 行 n 列。ここで、m は行のサイズ、n は列のサイズ。	symmatrix
シンボリック行列関数 ("R2022a 以降")	syms X Y [2 2] matrix syms f(X,Y) [2 2] matrix keepargs f(X,Y) = X*Y - Y*X f(X, Y) = X*Y - Y*X	size(f) などの未評価の行列関数のサイズは 1 行 1 列。 size(f(X,Y)) などの評価済み関数のサイズは m 行 n 列。ここで、m は行のサイズ、n は列のサイズ。	class(f) などの未評価の行列関数のデータ型は symfunmatrix。 class(f(X,Y)) などの評価済み関数のデータ型は symmatrix。

参考

syms | sym | symfun | symmatrix | symfunmatrix | symfunmatrix2symfun | symmatrix2sym | str2sym

関連するトピック

• シンボリック数、シンボリック変数およびシンボリック式の作成
• シンボリック関数の作成
• シンボリック行列の作成
• シンボリック行列変数の作成
• 関数 syms または sym の選択
• 数値演算またはシンボリック演算の選択